行星和卫星的距离分布

行星和卫星的距离分布

行星的轨道半长径——也就是行星和太阳的平均距离的分布具有一定的规律性，每个行星的a值同比它更靠近太阳的相邻行星的a值的比率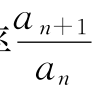大致是常数。对于规则卫星也有类似的情况。

对于天卫，比率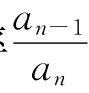都在1．46附近；对于土卫，去掉土卫八和土卫九这2个不规则卫星，则7个比率中只有1个较大，其余6个都在1．24附近；对于木卫五和木卫一到四，有3个比率很接近1．60，1个比值较大（达2．33）。对于行星，比率在1．69左右，偏差约20%。总的说来，对于行星和规则卫星，比率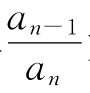大致为常数，即离中心体越远，相邻两个绕转体的轨道相隔也越远；对于不规则卫星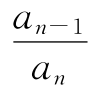，值明显地较大，即上述规律不适用于不规则卫星。

对于行星，距离分布规律还可以用另外一种方式来表示，这就是德国数学教师提丢斯在1766年发现的规律。以后几年，德国天文学工作者波得对此规律加以论述和宣传，后来被人们称作提丢斯—波得定则。行星离太阳的距离，如果用0．1天文单位来表示，可以用一个简单的数列写出：4，4＋3，4＋3×2，4＋3×2²，4＋3×2³……。把这条规律写成公式，就是

a_n＝0．4＋0．3×2^n－2天文单位。

在此公式中，当n＝1时，即对于水星，n－2不能取－1，而应当取－∞，即公式右边第二项完全不要。水星的实际a值是0．387，和公式给出的0．4差不多。n＝2，3，4时，公式给出的a值0．7，1．0和1．6同金星、地球和火星的a值0．723，1．0和1．523很接近。但n＝5时，公式给出的a值2．8和木星的a值5．203相差很多；只有当n＝6时，公式给出的值5．2才和木星的a值很接近。n＝7时，公式给出的值10．0和土星的a值9．52相差不太多。在提丢斯—波得定则提出来时，已知的最远行星是土星。在1781年，天王星被发现，算出的a值是19．2，同定则给出的值19．6相差不多。这样，就鼓励了天文工作者去努力寻找n＝5的位于火星轨道和木星轨道之间的行星。寻找结果，于19世纪初发现了好些个小行星，而不是一个大行星。头3个小行星的平均a值为2．7，和n＝5时公式给出的2．8很接近。不过，1846年发现的海王星和1930年发现的冥王星的a值，分别同n等于9和10时由公式给出的值相差很多。