导航常用坐标系
无人机导航中常见的坐标系如下:
(1)地球中心坐标系(Earth Centered Earth Fixed Coordinate System,ECEF);
(2)WGS-84大地坐标系(World Geodetic System-1984 Coordinate System,WGS-84);
(3)2000国家大地坐标系(China Geodetic Coordinate System 2000,CGCS2000);
(4)导航坐标系(如North-East-Down Coordinate System,NED);
(5)机体坐标系。
这些坐标系可分成地理坐标系和直角坐标系两类,其中地理坐标系和前述球面坐标系类似。导航坐标系中的地球中心坐标系、导航坐标系、机体坐标系都属于直角坐标系,而WGS-84大地坐标系和2000国家大地坐标系则属于地理坐标系。
1.地理坐标系
地理坐标系基于球面来定义地球上某点的位置。如图2-5所示,点的位置可表示为(L,B,H),L表示方位角,也称为经度,对于绝大多数地理坐标系,设定经过伦敦格林尼治天文台的子午线为零度经线,零度经线也称为本初子午线;B表示高度角,也称为纬度,以赤道为零度纬线;H表示相对高度。地理坐标系包括角度测量单位、本初子午线和基于旋转椭球体的基准面。
可通过经度值和纬度值对点进行引用,经度和纬度是从地心到地球表面上某点的测量角,通常以度或百分度为单位来测量该角度。图2-6将地球显示为具有经度值和纬度值的地球,从图中可以看出,水平线是纬线,垂直线是经线,这些线包裹着地球,构成了一个称为经纬网的格网化网络,经纬网的原点(0,0)定义在赤道和本初子午线的交点处。
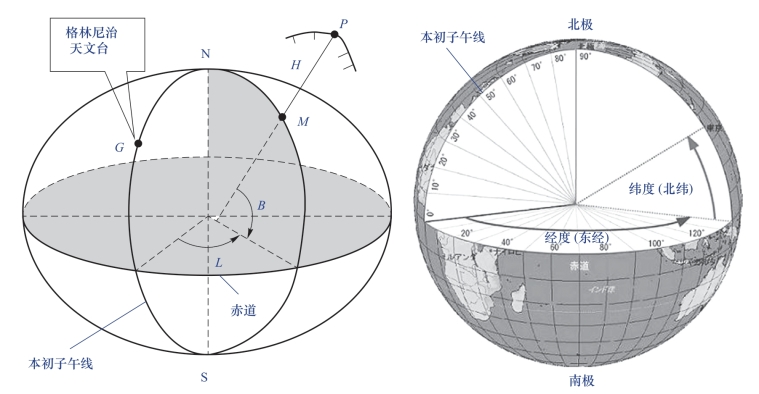
图2-5 地理坐标系
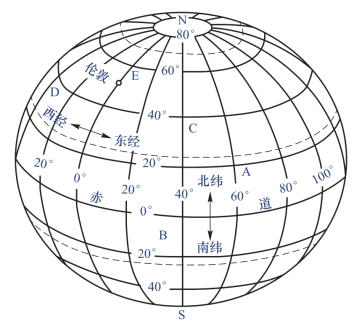
图2-6 地球仪上的经纬网
(1)参考椭球面。
由于地球是一个赤道略鼓、两极略扁的、球内各点密度不同,形状与梨的外形相似的不规则球体(图2-7),而且由于高山、悬崖、峡谷等地形地貌的存在,地球表面存在无数的凸起和凹陷,这就意味着不能用一个球体或者椭球体来完全拟合地球。由于地球表面71%的面积被海水覆盖,可以假设当海水处于完全静止的平衡状态时,从海平面延伸到所有大陆内部,而与地球重力方向处处正交的一个连续、闭合的曲面,该曲面是重力等位面,即水在这个面上不会流动,所以人们将其命名为大地水准面。但是由于地球表面起伏不平和地球内部质量分布不匀,故大地水准面是一个略有起伏的不规则曲面,人们常用来它表示地球的物理形状。
由于大地水准面不能用空间几何和数学公式很好地描述,我们需要对其进行再一次的逼近。大地水准面虽然十分复杂,但从整体来看,起伏是微小的,且形状接近一个扁率极小的规则椭球体。所以,可以引入参考椭球体作为大地水准面的近似,地球的参考椭球体是用空间几何及数学公式定义的近似匹配地球真实表面的椭球体(图2-8),而忽略了地表的地貌特征。
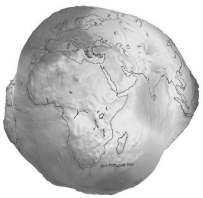
图2-7 真实的地球
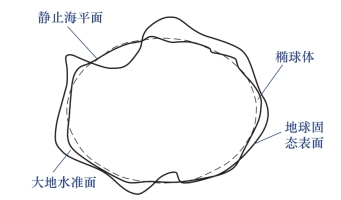
图2-8 拟合的椭球体
从图中可以看出旋转椭球体是由椭圆绕其长半轴或者短半轴旋转一圈得到的球体,所以,用以描述参考椭球体的关键参数为长半轴a和短半轴b(图2-9)。
另外,旋转椭球体还可以由长半轴和扁率来描述,扁率描述的是长半轴和短半轴的差异程度,一般用(a-b)/a表示。
(2)基准面。
由于地球真实形状的不规则性,导致没有一个标准的参考椭球体可以对地球上的每一点进行精准的量测,参考椭球体只是对真实地球表面的一种近似。参考椭球体可能与大地水准面的某些位置能够精确的拟合,但对另外一些位置的拟合相差甚远(图2-10)。因此,这里还需要一个大地基准面来控制参考椭球体和地球的相对位置。
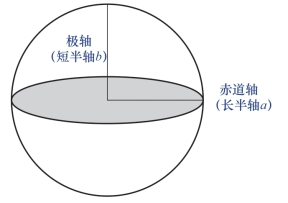
图2-9 椭球体参数
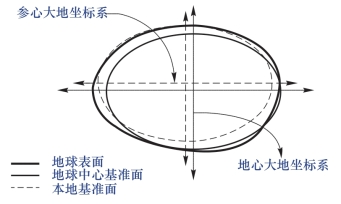
图2-10 地心基准面和区域基准面
当一个旋转椭球体的形状与地球相近时,基准面用于定义旋转椭球体相对于地心的位置,是基于特定参考椭球体通过位于特定位置的原点及方位角等参数对地球进行拟合。基准面定义了旋转椭球体逼近地球某一个区域表面的方式。每个国家和地区都有各自的基准面,每张地图与空间数据集都有基准面。基准面有很多,分别被用于地球上的不同位置。基准面可分为地心基准面和区域基准面。
1)地心基准面用于定义与地球最吻合的、坐标与地球质心相关联的旋转椭球体,其使用地球的质心作为原点,所以得到的椭球体又称地心大地坐标系。使用最广泛的地心基准面是WGS-84和CGCS2000,可用于世界范围内的定位测量。
2)区域基准面是在特定区域内与地球表面极为吻合的旋转椭球体。旋转椭球体表面上的点与地球表面上的特定位置相匹配。该点也被称为大地原点,大地原点的坐标是固定的,所有其他点由其计算获得。我们国家的区域基准面有北京54和西安80,其中,西安80的坐标原点(中华人民共和国大地原点),位于陕西省泾阳县永乐镇北流村(图2-11),其经纬度为北纬34°32′27.00″、东经108°55′25.00″。因为区域基准面的旋转椭球体仅与地表某特定区域吻合,所以不适用于该区域之外的其他区域。相对于同一地理位置,不同的大地基准面,其经纬度坐标是有差异的。由于椭球体的中心不与地球质心重合而是接近地球质心,所以基于区域基准面得到的坐标系又称为参心大地坐标系。

图2-11 中华人民共和国大地原点
(3)常见地理坐标系。
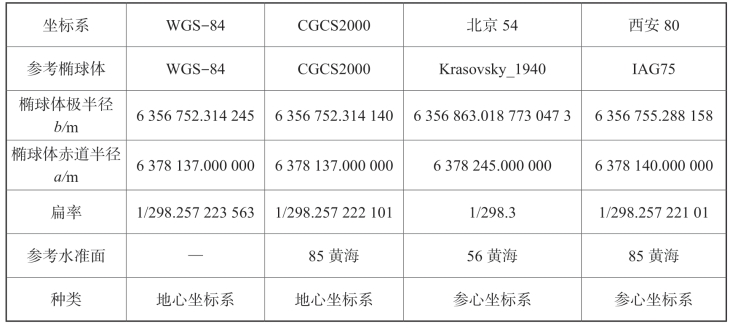
有了参考椭球体和大地基准面就可以建立地理坐标系了。地理坐标系是大地测量中以参考椭球面为基准面建立起来的坐标系。地面点的位置用经度、纬度和大地高度表示。表2-1列举了常见地理坐标系参数。
表2-1 常见地理坐标系参数
1)WGS-84大地坐标系是一种国际上采用的地心坐标系,GPS输出的就是这个坐标系下的坐标数据。坐标原点为地球质心,其地心空间直角坐标系的Z轴指向国际时间局(BIH)1984.0定义的协议地极(CTP)方向,X轴指向BIH 1984.0的协议子午面和CTP赤道的交点,Y轴与Z轴、X轴垂直构成右手坐标系,称为1984年世界大地坐标系。这是一个国际协议地球参考系统(ITRS),是目前国际上统一采用的大地坐标系(图2-12)。
2)2000国家大地坐标系是我国新一代大地坐标系,以国际地球框架ITRF 1997为参考,采用2000历元建立的区域性地心坐标系统于2008年正式启用。2000国家大地坐标系的原点为包括海洋和大气的整个地球的质量中心;2000国家大地坐标系的Z轴由原点指向历元2000.0的地球参考极(IERS参考极)的方向,该历元的指向由国际时间局给定的历元为1984.0的初始指向推算,定向的时间演化保证相对于地壳不产生残余的全球旋转,X轴由原点指向格林尼治参考子午线与地球赤道面(历元2000.0)的交点,Y轴与Z轴、X轴构成右手正交坐标系(图2-13)。(https://www.daowen.com)
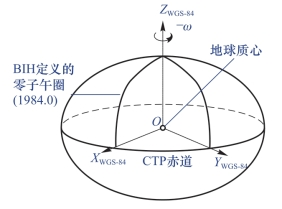
图2-12 WGS-84大地坐标系
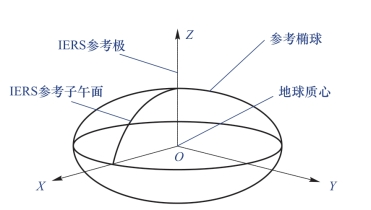
图2-13 CGCS2000坐标系
2.直角坐标系
(1)导航坐标系。常用的导航坐标系有东北天坐标系(ENU坐标系)和北东地坐标系(NED坐标系)两种。
对于在地球表面运动范围不大的无人机来说,其飞行区域接近于平面。要了解以操控者或地面站为中心的无人机导航信息,就需要建立位于地球表面的坐标系,来描述无人机的位置和速度。这里一般选用东北天坐标系作为无人机的一种导航坐标系,该坐标系的具体定义为:原点位于当地参考椭球的球面上,X轴沿参考椭球的纬线切线方向指向东(图2-14中的East方向),Y轴沿参考椭球经线切线方向指向地球北极(图2-14中的North方向),Z轴沿参考椭球面法线方向指向天顶(图2-14中的Up方向)。
在无人机开源飞控Pixhawk的原生固件PX4中采用的是北东地坐标系,北东地坐标系各轴的定义为:原点位于当地参考椭球的球面上,X轴沿参考椭球的纬线切线方向指向东(图2-15中的East方向),Y轴沿参考椭球经线切线方向指向地球北极(图2-15中的North方向),Z轴沿参考椭球面法线方向指向下方或者由右手定则确定(图2-15中的Down方向)。
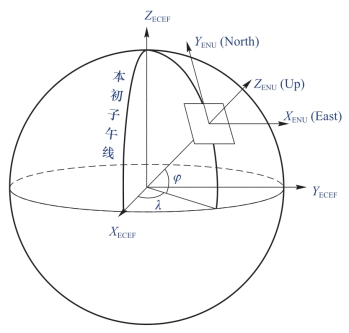
图2-14 东北天坐标系
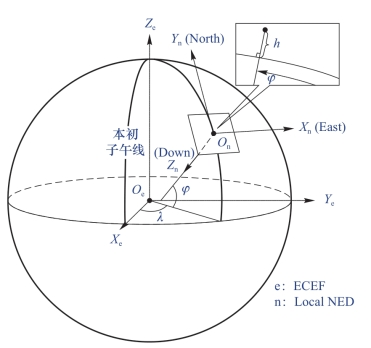
图2-15 北东地坐标系
(2)机体坐标系。在无人机的导航信息中,无人机的姿态参数非常重要,而想要很好地描述无人机的姿态,就离不开无人机机体坐标系。无人机机体坐标系是以无人机为中心,且固连在无人机上的坐标系,符合右手定则(图2-16)。具体定义:机体坐标系的原点位于无人机的质心,X轴沿无人机的纵轴方向向前(指向无人机机头方向),Y轴垂直于无人机对称面并指向飞行器右方,Z轴在对称面内垂直于XOY平面,且指向无人机下方。机体坐标系是无人机惯性导航的基础坐标系,IMU中获得的加速度状态信息就是该坐标系下的数值。

图2-16 机体坐标系
【任务实施】
方案的基本思路是先将两个WGS-84坐标系下的坐标位置转换到地心地固坐标系ECEF中,并计算两个点在ECEF坐标系中的坐标差,而后将ECEF中的坐标差转换至东北天坐标系中。
设飞机起飞点在WGS-84坐标系的坐标P0=[lat0,lon0,hgt0]T,农田区域某点的GPS坐标P1=[lat1,lon1,hgt1]T。则可以求出起飞点在ECEF中的坐标[X0,Y0,Z0]T:
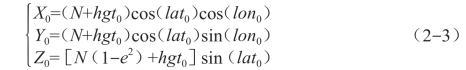
式中,e为WGS-84椭球偏心率,N为基准椭球体的曲率半径,各自表达式如下:

式中,a为椭球长半轴,b为椭球短半轴。
同理,可以计算出点在ECEF坐标系下的坐标[X1,Y1,Z1]T。
WGS-84坐标系转换至ECEF坐标系可以通过COORD GM软件计算(图2-17),先在源坐标类型选择框里选中大地坐标,在目标坐标类型中框选空间直接坐标,在椭球下拉列表中都选择WGS-84;在源坐标输入框中输入想转换的经纬度和高程信息;最后单击“转换坐标”按钮,就可以得到转换后的空间直角坐标。
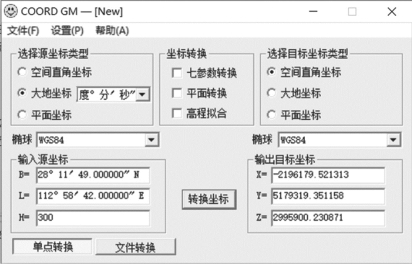
图2-17 坐标系转换
然后可以求出,两点在ECEF坐标系下的坐标差:

最终点在北东天坐标系的坐标为
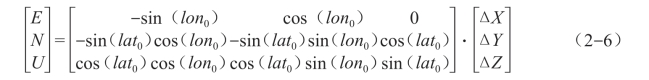
COORD GM软件除了可以实现大地坐标系到空间直角坐标系的坐标转换,还可以实现WGS-84大地坐标系到西安80坐标系的转换,但是需要转换参数。而转换参数属于保密数据,因此无法通过其参数实现坐标转换,只能找控制点,通过控制点实现坐标转换。由于测绘数据属于国家机密,在野外使用无人机进行测绘作业时,应提前向当地政府主管部门申请,严禁利用无人机进行非法测绘。
【拓展阅读】
笛卡尔坐标系的由来
经典名言“我思故我在”的提出者,法国哲学家、数学家笛卡尔,据说有一天,生病卧床,病情很重,尽管如此,他还反复思考一个问题:几何图形是直观的,而代数方程是比较抽象的,能不能把几何图形与代数方程结合起来,也就是说,能不能用几何图形来表示方程呢?要想达到此目的,关键是如何把组成几何图形的点和满足方程的每一组“数”挂上钩,他苦苦思索,拼命琢磨,通过什么样的方法才能把“点”和“数”联系起来呢?突然,他看见屋顶角上的一只蜘蛛,拉着丝垂了下来,一会儿工夫,蜘蛛又顺着丝爬上去,在上边左右拉丝。蜘蛛的“表演”使笛卡尔的思路豁然开朗。他想,可以把蜘蛛看作一个点,它在屋子里可以上、下、左、右运动,能不能把蜘蛛的每个位置用一组数确定下来呢?他又想,屋子里相邻的两面墙与地面交出了3条线,如果把地面上的墙角作为起点,把交出来的3条线作为3根数轴,那么空间中任意一点的位置就可以从这3根数轴上找到有顺序的3个数。反过来,任意给一组3个有顺序的数也可以在空间中找出一点P与之对应,同样的道理,用一组数(x,y)可以表示平面上的一个点,平面上的一个点也可以用一组2个有顺序的数来表示,这就是坐标系的雏形。
17世纪初,笛卡尔建立了他的坐标系。今天,在我们看来,坐标系十分简单。可就是这么简单的坐标系,对数学产生了极其重要的影响,凭着这一项发明,笛卡尔跻身数学帅才之列。笛卡尔坐标系厉害在哪里呢?有人可能会说数和形统一起来了,也有人会说解析几何从此诞生了。这些说法都是对的,但笛卡尔坐标系的真正意义不止于此。笛卡尔提出坐标系,并没有证明深刻的定理,但坐标系对数学发展的影响是任何深刻的定理都比不了的,因为有了坐标系,才会有变量,才可以表达函数,微积分才有了发展的舞台。与古代常量数学不同,资本主义萌芽之后的数学是变量数学的时代,这源于实践中提出的对运动研究的要求。笛卡尔坐标系是变量数学的先导和基础,这是坐标系的真正意义,深刻地影响了数学的发展。
【巩固提高】
1.我们国家的北斗卫星导航系统采用的坐标系是什么?
2.无人机导航中用到的坐标系有哪些?
3.查找资料,简要描述GPS卫星导航系统采用的坐标系。
4.简述六旋翼无人机的机体坐标系。
