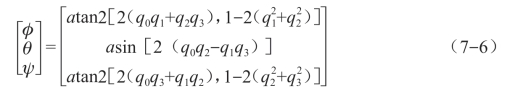一、姿态表示
现在假设无人机从刷新后的返航点起飞，并在空中完成各种动作，如俯仰、偏航、横滚等。这就牵涉两个坐标系，即导航坐标系和机体坐标系。导航坐标系的原点就是返航点；而机体坐标系固连于无人机。无人机飞行姿态和这两个坐标系相关，那怎么描述飞机的姿态呢？
1.方向余弦矩阵
如图7-1所示，导航坐标系定义为Oxyz，机体坐标系定义为OXYZ，两坐标系具有相同的原点O。导航坐标系X、Y、Z轴对应的单位向量分别为I、J、K；机体坐标系的x、y、z轴对应的单位向量分别为i、j、k。
则机体坐标系的向量i在导航坐标系下可表示为：iN=
，其在导航坐标系X轴的分量的大小即向量i在X轴上的投影长度，可表示为：
，同理可写出向量i在Y轴和Z轴上投影长度：
，
。最终iN=［cos（I，i），cos（J，i），cos（K，i）］T。
类似地，jN可表示为jN［cos（I，j），cos（J，j），cos（K，j）］T。kN可表示为kN=［cos（I，k），cos（J，k），cos（K，k）］T，由于这些分量都是用余弦表示，所以它们组成的矩阵称为余弦矩阵，可表示为
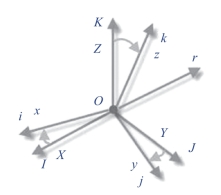
图7-1 导航坐标系和机体坐标系
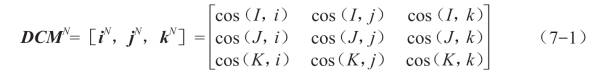
这样，机体坐标系下的坐标位置经由余弦矩阵就能变换到导航坐标系下的坐标位置，可用下式表示：
而由导航坐标系变换到机体坐标系下的余弦矩阵为DCMN转置矩阵。
由上可以看出，余弦矩阵的参数量有9个，要求9次向量内积，便于计算机处理的，计算量大，实时性不好；另外，余弦矩阵不可以直接插值，冗余信息多，同样不直观。
2.欧拉角
欧拉角是由瑞士数学家欧拉首先提出来的，代表一系列的三维基本旋转，可用于描述导航坐标系到机体坐标系的过程中绕3个坐标轴旋转的角度。这里的坐标轴既可以是导航坐标系下的，也可以说是机体坐标系的，而且旋转顺序任意。
任何一个方向都可以使用3个方向的基本旋转描述出来，一个基本旋转既可以是一个绕着固定坐标系中的轴旋转，也可以绕一个随无人机转动的坐标系的轴旋转。所以，欧拉角可分为以下两种情况：
（1）静态：即绕导航坐标系3个轴的旋转，也称为外旋。由于物体旋转过程中坐标轴保持静止，所以称为静态（图7-2）。
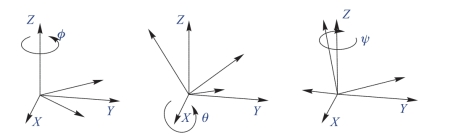
图7-2 绕导航坐标系的坐标轴旋转
（2）动态：即绕机体坐标系3个轴的旋转，也称为内旋。由于物体旋转过程中坐标轴随着无人机做相同的转动，所以称为动态（图7-3）。
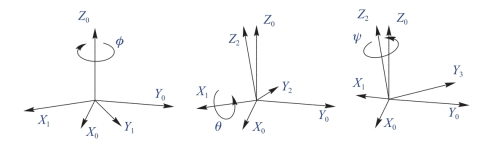
图7-3 绕机体坐标系的坐标轴旋转
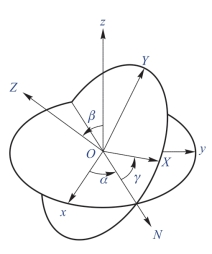
如图7-4所示，O-xyz为导航坐标系，固定不动；O-XYZ为机体坐标系，可随无人机一起转动。刚开始时，导航坐标系与机体坐标系完全重合，则导航坐标系可通过以下步骤旋转至机体坐标系：首先，无人机绕导航坐标系的z轴旋转α角，此时机体坐标系的X轴和ON轴重合；其次，无人机绕机体坐标系的X轴（ON轴）旋转β角；最后，无人机绕机体坐标系的Z轴旋转γ角，即可完成从导航坐标系到图中机体坐标系的旋转动作。
图7-4 欧拉角
两坐标系之间的关系可用下式表示：
其中，M为旋转矩阵，可表示为
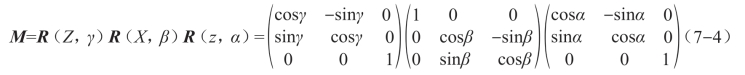
如果改变上述旋转步骤顺序，显然得到的最终结果不一样。我们把上述旋转步骤按照顺序标记为zXZ，第一个“z”为导航坐标系的坐标轴，后面的“X”和“Z”为机体坐标系的坐标轴。坐标轴旋转顺序加上绕每个坐标轴旋转的角度，就是一个完整的欧拉角：zXZ-（α，β，γ）。
对不同的问题，宜选取不同的轴做基本轴，并按不同的方式量取欧拉角。没有约定好旋转轴顺序和坐标系选择的欧拉角是没有意义的。这里有12种绕轴旋转的方式，在不区分外旋和内旋的情况下，可以分为以下两类：
（1）经典欧拉角：zXZ、xYX、yZY、zYZ、xZX、yXY。一般用内旋zXZ序列来描述无人机的姿态，其中，第一次绕导航坐标系的z轴（也是机体坐标系的Z轴）旋转为偏航，第二次绕机体坐标系的X轴旋转为俯仰，第三次绕机体坐标系的Z轴旋转为滚转。
（2）泰特-布莱恩角：XYZ、YZX、ZXY、XZY、ZYX、YXZ。一般用内旋ZYX序列来描述无人机的姿态，其中，绕Z轴旋转为偏航，绕Y轴旋转为俯仰，绕X轴旋转为滚转。
用欧拉角表示方向只需要用到3个参数，即3个旋转角度，这样做的好处是清晰易懂。但随之而来的问题是，当给定了欧拉角后，很容易得到表述的方向；但反过来，给定无人机的方向后，不一定能写出与之对应的唯一的欧拉角，三维空间中的任意一个方向都可以通过至少两种不同欧拉角表示。例如欧拉角zXZ-（0°，0°，0°）和zXZ-（10°，0°， -10°）表示的是同一个目标方向（图7-5）。
另外，欧拉角还存在万向节死锁问题，如采用欧拉角xYZ-（φ，θ，ψ）来描述无人机的旋转运动，当俯仰角为±90°，则无人机的自由度就会由三自由度变为二自由度，无人机失去了横滚自由度，意味着第一次旋转和第三次旋转等价。例如，xYZ-（10°，90°，20°）和xYZ-（20°，90°，10°）表示相同的方向，此时，绕X轴旋转与绕Z轴旋转没有区别。
图7-5 欧拉角xYZ-（φ，θ，ψ）
3.四元数
欧拉角由于存在死锁，且不适合插值和迭代，不适合无人机的大姿态角飞行。之后，英国数学家哈密顿发明了四元数，用四维向量来描述物体在三维空间的姿态及姿态变化，就这样完美地解决了死锁问题，而且四元数只用到了4个参数，能够减少计算量和存储空间。
四元数可用下式表示：
其中，向量v=（vx，vy，vz）为旋转轴，θ为旋转的角度，旋转遵从右手法则，而且四元数的模|q|=1（图7-6）。
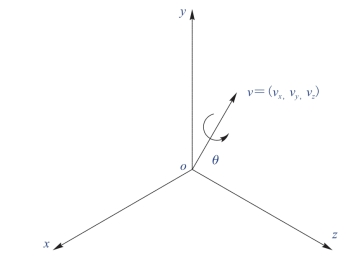
图7-6 四元数
可通过四元数求得欧拉角，关系式为
