二、互补滤波
1.工作原理
无人机姿态的测量主要通过加速度计、陀螺仪和磁力计得到，但是这些传感器各有优缺点。其中，陀螺仪直接测量的是无人机绕机体坐标系坐标轴旋转的角速度，在小角度的情况下，角速度积分就可以得到姿态角，可用于姿态的连续更新，优点是几乎不受外界因素干扰，动态性能好；缺点是由于噪声等误差影响，在积分作用下形成累积误差，导致陀螺仪有低频干扰和漂移，长时间工作，姿态角数据会非常不准确。
加速度计和磁力计分别测量的是无人机机体坐标系下3个坐标轴方向的加速度和磁场分量，两者都可直接用于姿态的测量。其优点是静态性能好，不存在累积误差；缺点是容易受外界干扰。例如，加速度计对高频信号敏感，导致振动环境对加速度计有较大的高频干扰，并且仅在无人机静止或匀速运动时，加速度计测量姿态才准确；而磁力计容易受磁场干扰，导致测量的航向角不准。
由此可以看出，单一使用任何传感器，都无法得到有效准确的航向角和姿态角。因此，需要同时使用多个传感器，结合各自优缺点，将其数据进行融合，从而得到最准确的估计。
通过以上分析，可以得知陀螺仪易受低频干扰，而加速度计易受高频干扰，磁力计可以辅助得到航向角。如果把它们的噪声分别滤除，然后合并，就能得到没有噪声的姿态信息。这就是互补滤波的思想，而“互补”体现在低通滤波器和高通滤波器合并后能通过完整的波形，也就是波形完全不变，是全通的（图7-7）。得益于这些传感器在频域上特性互补，所以可采用互补滤波融合这些传感器的数据，从而提高测量精度和系统的动态性能。
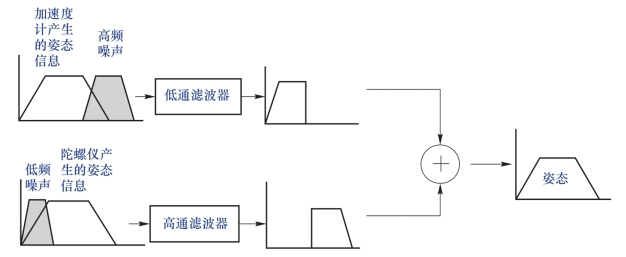
图7-7 互补滤波的滤波过程
在Pixhawk飞控中，姿态互补滤波的使用有以下一些前提条件：
（1）无人机处于悬停状态，或是接近匀速运动，即无人机不是处于高机动或大姿态角运动状态。
（2）两路信号的测量数据包含的干扰噪声处在不同的频率范围，一路干扰噪声为低频，另一路必须为高频。
（3）航姿数据的更新满足线性关系。
2.滤波器
在Pixhawk飞控的姿态估计中，互补滤波对陀螺仪（低频噪声）使用高通滤波器；对加速度/磁力计（高频噪声）使用低通滤波器。
低通滤波器（LPF）和高通滤波器（HPF）的传递函数可用下式表示：
Pixhawk飞控采用的是二阶滤波器，即
式中，Kp为比例系数，Ki为积分系数。
互补滤波可用图7-8所示的框图表示。
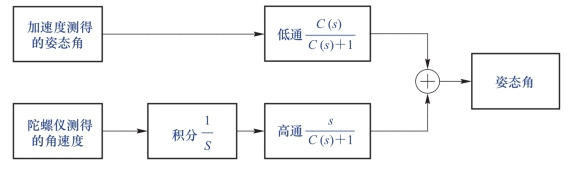
图7-8 互补滤波框图
设加速度测得的姿态角用acc_rpm表示，陀螺仪测得的角速度用gyr_ωm表示，滤波后的姿态角用att_rp表示，则由上面的框图可得
基于负反馈思想，可将式（7-9）用图7-9表示。
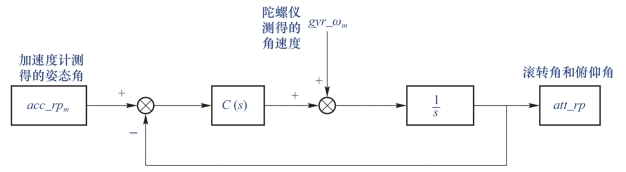
图7-9 姿态估计
加上磁力计测得的地磁数据，最终基于互补滤波的航姿估计流程图，如图7-10所示。
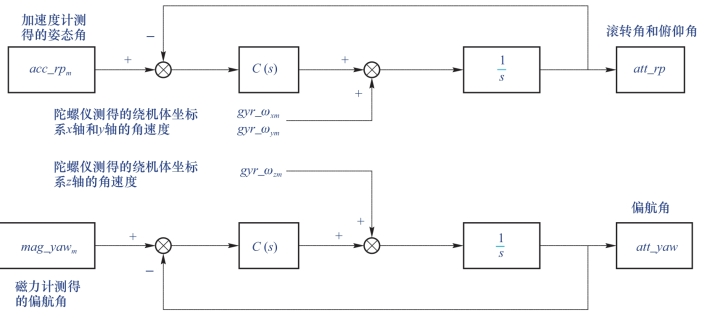
图7-10 航姿估计
由图7-10可以看出，互补滤波除要考虑滤波器参数外，还要求取姿态角和航向角的差值。
3.误差的求取
对于一个确定的向量，用不同的坐标系表示时，它们所表示的大小和方向一定是相同的。但是由于这两个坐标系的转换矩阵存在误差，那么当一个向量经过一个有误差的旋转矩阵变换后，在另一个坐标系中肯定和理论值是有偏差的，所以需要将这个偏差进行反馈，从而修正这个旋转矩阵。这个偏差可以通过加速度计和磁力计来表征，然后通过算法修正误差，修正四元数，最终达到修正航向和姿态的目的。
（1）使用加速度计修正俯仰角和滚转角。在导航坐标系中，标准重力加速度为大小为g，对其进行归一化处理得到，重力矢量为：an=［0，0，1］T。则该矢量在机体坐标系下可表示为
，其中
为转换矩阵，用四元数可表示为
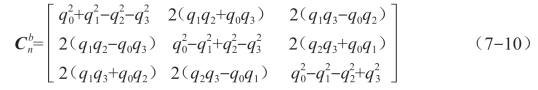
而无人机加速度计测得的三轴加速度就是无人机在机体坐标系下的加速度，设归一化后的测量值为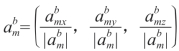
，理论上
应该与ab相等，但在实际情况中，由于转换矩阵总存在误差，所以往往不相等。对
和ab做向量叉乘，即可得到陀螺仪的校正补偿值
，然后就可以修正旋转矩阵
了。
（2）使用磁力计修正偏航角。由于加速度计无法感知无人机绕导航坐标系Z轴的旋转运动，因此还需要磁力计进一步补偿。现假设
是经过加速度计校正后的旋转矩阵，而磁力计在机体坐标系下的测量矢量为
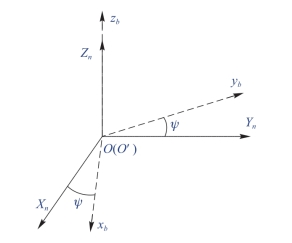
，该向量经过旋转矩阵转换至导
，mn的x轴和y轴分量组成的平面会和导航坐标系的XOY平面重合，即把机体坐标系的数据，变成了水平机体坐标系，也就是机体水平的情况下，磁力计测量的数据值，这时只存在一个绕导航坐标系旋转的偏航角误差（图7-11）。航坐标系后，可得到
图7-11 偏航角误差
由于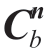
只是修正了俯仰角和偏航角，而并未修正偏航角，所以该旋转矩阵只在Z轴上存在一个偏航的误差，这就导致
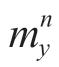不为0。假定理想情况下，让导航坐标系中x轴指向正北方向，那么地磁向量y轴方向为0，则在导航坐标系下磁力计数据为
该向量为地磁向量绕Z轴旋转一定的角度后得到的，绕Z轴旋转不改变向量在XOY平面的投影的大小。将地磁向量在导航坐标系中的理想输出，再次旋转到载体坐标系中，得到在载体坐标系中的理想输出：
由于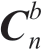
还存在偏航角误差，所以
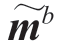和mb并不相等，将理想输出和原始输出做叉积得到误差
，将其作为补偿项送给陀螺仪进行偏航校正。
这样总的校正补偿量为e=ea+em。然后使用PI控制器进行滤波，消除陀螺仪漂移误差，只要存在误差，控制器便会持续作用，直至误差为0。控制的效果取决于比例参数Kp和积分参数Ki。PI控制的公式如下：
用得到的控制量对陀螺仪输出的数据进行校正，然后通过四元数微分方程式（7-10）获得校正后的四元数。
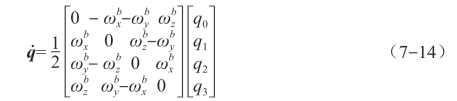
其中，分别为陀螺仪在机体坐标系下测得的无人机绕x、y、z轴的角速度。
这样欧拉角就可以由校正后的四元数求出。
【任务实施】
1.可用的估计器
Px4固件中，可用的估计器名称及用途如下：
（1）attitude_estimator_q。attitude_estimator_q是基于四元数的姿态估计器。其方法简单，采用的是互补滤波算法。
（2）position_estimator_inav。position_estimator_inav为惯导位置估计器，它使用互补滤波对三维位置以及速度进行估计。
（3）local_position_estimator。local_position_estimator为位置估计器，其使用的是扩展卡尔曼滤波，能对三维位置以及速度进行估计。
（4）EKF2。EKF2使用扩展卡尔曼滤波对三维姿态、位置/速度以及风的状态进行估计。
2.如何使能不同的估计器
对于多旋翼和垂直起降飞行器，使用参数SYS_MC_EST_GROUP在下列配置中进行选择（表7-1）。
表7-1 配置状态估计器
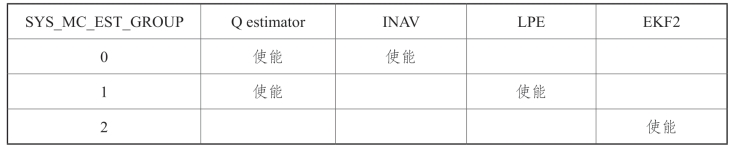
如果希望多旋翼无人机使用互补滤波器来估计速度和位置，可以在Mission Planner全部参数表里查找SYS_MC_EST_GROUP参数，并将其设为0，然后重新启动飞控即可（图7-12）。
图7-12 SYS_MC_EST_GROUP参数
【拓展阅读】
多传感器信息融合——不确定推理方法
在多传感器信息融合系统中，各传感器提供的信息一般是不完整、不精确、模糊的，甚至有时可能是矛盾的，即包含着大量的不确定性。信息融合中心不得不依据这些不确定性信息进行推理，以达到目标身份识别和属性判决的目的。不确定性推理是目标识别和属性信息融合的基础。不确定性推理也是一种建立在非经典逻辑基础上的基于不确定性知识的推理，它从不确定性的初始证据出发，通过运用不确定性知识，推出具有一定程度的不确定性和合理的或近乎合理的结论。
不确定性推理包括符号推理和数值推理：前者的特点是在推理过程中信息损失较少，但计算量较大；后者的典型代表是D-S证据理论，其特点是易于实现，但在推理过程中有一定的信息损失。
D-S证据理论全称“Dempster-Shafer证据理论”，源于美国哈佛大学数学家A.P.Dempster在利用上、下限概率来解决多值映射问题方面的研究工作。后来他的学生G.Shafer引入信任函数的概念，形成了一套基于“证据”和“组合”来处理不确定性推理问题的数学方法。
证据理论的优点：在证据理论中需要的先验数据容易获得；Dempster合成公式可以综合不同专家或数据源的知识或数据，用途广泛。
证据理论的缺点：要求证据必须是独立的，有时不易满足；证据合成规则没有非常坚固的理论支持，其合理性和有效性还存在较大的争议；计算上存在着潜在的指数爆炸问题。
【巩固提高】
1.在姿态解算过程中，为什么要进行传感器融合？
2.在互补滤波中，加速度计和磁力计的作用是什么？
3.什么是欧拉角？