一、静态相对定位
静态相对定位是指用两台接收机分别安置在基线的两个端点，其位置静止不动，同步观测4颗以上相同的卫星，解算基线向量，从而确定两个端点在协议地球坐标系中的相对位置的方法。
静态相对定位一般采用测相伪距观测值作为基本观测量。为了可靠地确定载波相位的整周未知数，一般需要1～3 h的观测时间，对于中等长度的基线（100～500 km），其精度可达10-6～10-7量级，是当前GPS定位中精度最高的一种方法。
在测相伪距观测中，首要问题是如何快速而精确地确定整周未知数。在确定好整周未知数后，随着观测时间的加长，相对定位的精度不会显著提高。因此，提高定位效率的关键在于快速而可靠地确定整周未知数。
由于当距离不太远的两个测站同步观测相同卫星时，GPS的各种观测误差具有较强的相关性，所以一种简单而有效的消除或减弱误差的方法是将GPS的各种观测量进行不同的线性组合，然后作为相对定位的相关观测量。这样做的好处是能消除或减弱一些系统性误差的影响，如卫星轨道误差、钟差、大气折射误差等，同时，也能减少平差计算中未知数的个数。
1.基本观测量
假设安置在基线端点的接收机T1和T2，在历元t1和t2，对GPS卫星Sj和Sk进行了同步观测，分别得到载波相位观测量：
、
。取符号Δφj（t）、Δφi（t）、
分别表示不同接收机之间、不同卫星之间和不同历元之间的观测量之差，则有
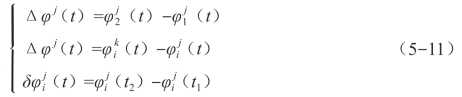
接收机观测卫星的载波相位观测量的表达式为
。
2.线性组合
目前普遍采用的线性组合形式有单差、双差和三差3种。
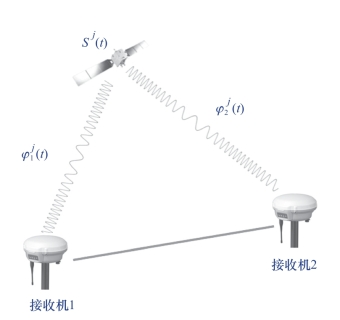
（1）单差观测方程。单差即在不同观测站，同步观测相同卫星所得观测量之差（图5-45）。其可表示为
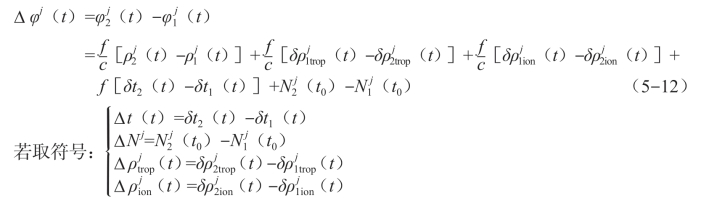
则单差方程可写为
由式（5-13）可以看出，卫星钟差的影响已经消除，这是单差模型的优点。两观测站接收机的相对钟差，对同一历元两站接收机同步观测量所有单差的影响均为常量。而卫星轨道误差和大气折射误差，对两站同步观测结果的影响具有相关性，其对单差的影响明显减弱。
图5-45 单差示意
如果对流层对独立观测量的影响已经根据实测大气资料利用模型进行了修正；电离层的影响也利用模型或双频接收机进行了修正，则载波相位观测方程中相应项，只是表示修正后的残差对相位观测量的影响。这些残差的影响在单差后会进一步减弱。
另外采用单差法，能使观测方程比独立观测时要少一半。
（2）双差观测方程。双差即在不同观测站，同步观测同一组卫星，所得单差之差（图5-46）。其可表示为
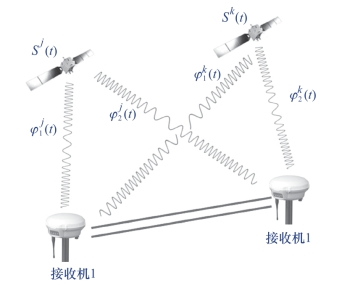
图5-46 双差示意
若忽略大气折射残差的影响，可得双差观测方程：
由式（5-15）可以看出，双差模型消除了接收机钟差的影响。另外，双差观测的必要历元数只与同步观测的卫星数有关，与观测站的数量无关。为了解算观测站的坐标未知数和载波相位的整周未知数，在两个或多个观测站同步观测4颗卫星时，必须至少观测两个历元。双差观测方程的缺点是可能组成的双差观测方程数进一步减少。如两个观测站， 两个历元，同步观测4颗卫星，独立观测量方程总数为16，双差观测方程仅为6个。
（3）三差观测方程。三差是在不同历元，同步观测同一组卫星，在双差的基础上进一步做差。其可表示为
将式（5-15）代入式（5-16）中可得
由式（5-17）可以看出，三差模型消除了整周未知数的影响，但使观测方程的数量进一步减少，这会对未知参数的解算可能产生不利影响。在实际定位中，一般采用双差模型加平差模型来求解未知参数。