双目视觉导航系统相关坐标系
1.像素坐标系
一帧640像素×480像素分辨率的灰度图包含307 200个像素，这里的640和480分别指图片的每一行和每一列的像素数量。为了描述某个像素点的位置，就需要一个坐标系，这个坐标系就叫作像素坐标系。
如图6-21所示，点O为像素坐标系的原点，点P0为图片某个像素点，其坐标为（u0，v0）， 横坐标u0和v0纵坐标分别是像素点所在的行和列。
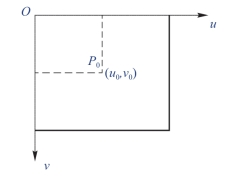
图6-21 像素坐标系
2.图像坐标系
如图6-22所示，图像坐标系的原点为O1，位于图片的正中心位置，横坐标为x轴，纵坐标为y轴，该坐标系下的点P1的坐标为（x，y）。
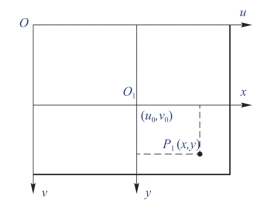
图6-22 图像坐标系
假设图像坐标系原点O1在像素坐标系下的坐标为（u0，v0），dx和dy分别表示每个像素在横轴x和纵轴y的物理尺寸。则图像坐标系和像素坐标系的转换关系为
写成矩阵形式为
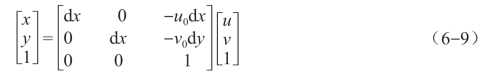
3.相机坐标系
相机坐标系是一个三维坐标系，是以相机投影中心OC为原点，XC和YC轴分别平行于图像的两条边，ZC轴为光轴。物体P在相机坐标系下的位置可表示为（XC，YC，ZC）（图6-23）。
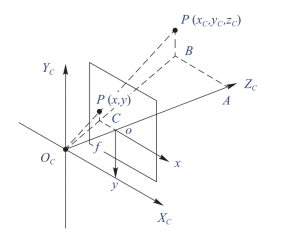
图6-23 相机坐标系
4.世界坐标系
在客观三维世界中，为了确定三维空间点的位置，需要确定唯一一个基准坐标系来描述空间物体的位置，这就是世界坐标系。世界坐标系可以根据运算方便性自由放置。在双目视觉中，世界坐标系主要有3个用途：
（1）标定时确定标定物的位置；
（2）作为双目视觉的系统参考系，给出两个相机相对世界坐标系的关系，从而求出相机之间的相对位置关系；
（3）作为重建得到三维坐标的容器，盛放重建后的物体的三维坐标。
如图6-24所示，世界坐标系的坐标原点为Ow，其余3个坐标轴分别为Xw、Yw、Zw轴，点P在世界坐标系中的位置为（Xw，Yw，Zw）。世界坐标系和相机坐标系之间的位置关系如图6-24所示。
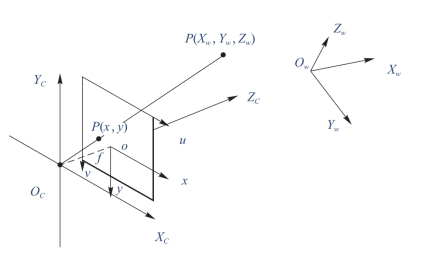
图6-24 世界坐标系和相机坐标系之间的位置关系
5.坐标系之间的变换
（1）图像坐标系和相机坐标系之间的转换。相机坐标系和图像坐标系之间的转换是在3D和2D之间转换，属于透视投影关系。
由图6-24可知：
式中，ZC为物体的深度信息。
可将式（6-10）写成矩阵形式：
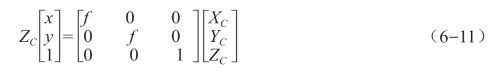
（2）世界坐标系和相机坐标系之间的转换。世界坐标系和相机坐标系之间的转换，涉及坐标系的旋转和平移，属于刚体变换，如图6-25所示，其中R表示旋转矩阵，即世界坐标系绕其坐标轴旋转后，便可使旋转后的世界坐标系的3个轴分别和相机坐标系的3个轴方向相同；T表示平移矢量，表示旋转后的世界坐标系经过平移后便可完全和相机坐标系重合。转换关系可用矩阵表示：
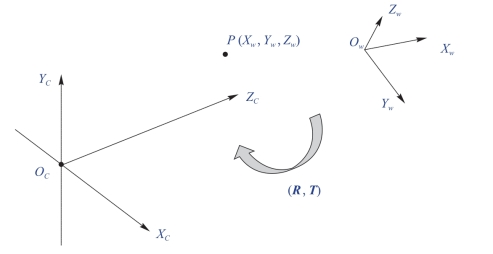
图6-25 世界坐标系和相机坐标系之间的转换
这样，通过坐标转换关系，便可建立图像像素点位置和对应的物点在世界坐标系中的位置关系：
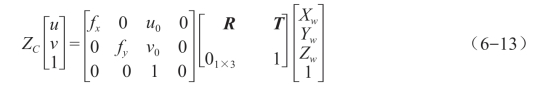
其中，
。等号右边的第一个矩阵称为相机的内参，第二个矩阵称为相机的外参。相机的内参和外参可以通过标定法获取。
6.相机的畸变参数
前面坐标系转换是基于相机的针孔模型，只是真实相机的一个近似，由于相机存在各种镜头的畸变和变形，会引起拍摄的图像发生变形，这会给后面的视差计算带来困难。为了减少图像变形带来的影响，需要测量镜头的畸变参数，从而对图像进行校正。常见的图像畸变有径向畸变和切向畸变两种。
（1）径向畸变。径向畸变是指图像像素以畸变中心为原点，沿着径向（镜头半径方向）产生位置偏差，离畸变中心越远，位置偏差越大，表现为图像弯曲越严重。径向畸变又可分为枕形畸变和桶形畸变（图6-26）。
径向畸变的数学模型可以用像主点周围的泰勒级数展开式的前几项进行描述，通常使用前两个参数，即k1和k2，对于畸变很大的镜头，如鱼眼镜头，可以增加使用第三项k3参数来进行描述，相机成像平面上某点的校正公式为
式中，（x0，y0）为未进行径向畸变校正前像点的位置，（x，y）为校正后像点的新位置。
（2）切向畸变。切向畸变是由于安装时，存在安装偏差，透镜本身与相机传感器平面（成像平面）或图像平面不平行而造成的（图6-27）。
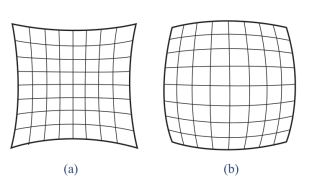
图6-26 径向畸变
（a）枕形畸变；（b）桶形畸变
图6-27 切向畸变
切向畸变模型可以用两个额外的参数p1和p2来描述。其校正公式为
这样，径向畸变和切向畸变模型中一共有5个畸变参数，这5个参数就是相机标定中需要确定的相机的5个畸变系数。求得这5个参数后，就可以校正由于镜头畸变引起的图像的变形失真。图6-28所示为畸变校正前后效果图。
图6-28 畸变校正
（a）校正前；（b）校正后