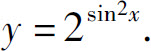1.1 函数
1.1 函数
1.1.1 集合
一般地,把具有某种特定性质的对象组成的总体称为集合,把组成集合的对象称为该集合的元素.
通常用大写字母A,B,C等表示集合,用小写字母a,b,c等表示元素.若a是集合A的元素,记为a∈A,否则记为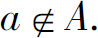 根据集合中元素个数的多少,集合可分为有限集和无限集.
根据集合中元素个数的多少,集合可分为有限集和无限集.
集合通常有两种表示方法:列举法和描述法.
(1)列举法.列举法是将集合的所有元素一一列举出来的表示方法.例如,由元素a1,a2,…,an组成的集合A可表示成
A={a1,a2,…,an}.
(2)描述法.若集合A是由具有某种性质P的元素的全体所组成,就可以表示成
A={x∣x具有性质P}.
例如,大于0小于6的一切实数组成的集合可表示成
M={x∣0<x<6,x∈R}.
习惯上,将全体非负数整数即自然数的集合记为N,全体正整数的集合记为N*,全体整数的集合记为Z,全体有理数的集合记为Q,全体实数的集合记为R.
如果集合A的每一个元素都是集合B的元素,则称A是B的子集,或B包含A,记为A⊂B(或B⊃A).例如有
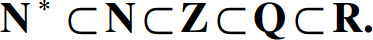
如果A⊂B且B⊃A,则称集合A与B相等,记为A=B.
不含任何元素的集合称为空集,记为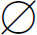 ,并规定空集为任一集合的子集.
,并规定空集为任一集合的子集.
1.1.2 实数集
区间与邻域是微积分学中常用的实数集.
设a和b为实数,且a<b.数集{x∣a<x<b}称为开区间,记为(a,b);数集{x∣a≤x≤b}称为闭区间,记为[a,b];数集{x∣a≤x<b}和{x∣a<x≤b}都称为半开半闭区间,分别记为[a,b)和(a,b].
以上这几类区间统称为有限区间,其中a,b分别称为区间的左端点和右端点,b-a称为区间的长度.
类似可定义无穷区间
[a,+∞)={x∣x≥a};
(a,+∞)={x∣x>a};
(-∞,b]={x∣x≤b};
(-∞,b)={x∣x<b};
(-∞,+∞)={x∣-∞<x<+∞}=R.
设有实数a及δ,且δ>0.称数集{x∣∣x-a∣<δ}为点a的δ邻域,记为U(a,δ).其中,a称为这个邻域的中心,δ称为这个邻域的半径,如图1.1所示.
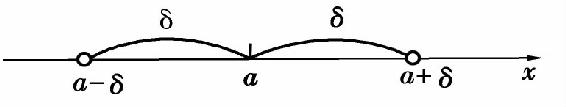
图1.1
称数集{x∣0<∣x-a∣<δ}为点a的去心δ邻域,记为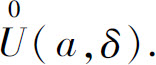 它是点a的δ邻域去掉中心点a所得的集合.
它是点a的δ邻域去掉中心点a所得的集合.
当不需要强调邻域的半径δ时,点a的δ邻域和去心δ邻域可分别简记为U(a)和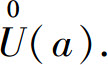
为了方便,把区间(a-δ,a)和(a,a+δ)分别称为点a的左δ邻域和右δ邻域.
1.1.3 函数的概念
定义1 设D是一个非空实数集,如果按照某一确定的对应法则f,对于每一个实数x∈D,都有唯一的一个实数y与之对应,则称对应法则f是定义在实数集D上的函数,记为
f:D→R或y=f(x),x∈D.
其中,x称为自变量,y称为因变量,D称为定义域.
每个x∈D所对应的数y称为函数f在点x的函数值,记为y=f(x).全体函数值的集合
f(D)={y∣y=f(x),x∈D}
称为函数f的值域.
函数概念的两个基本要素是对应法则和定义域.如果两个函数的定义域和对应法则都相同,则称这两个函数相同.
函数的定义域通常按以下两种情况来确定:一种是有实际背景的函数,其定义域根据这个问题的实际意义来确定;另一种是用数学表达式表示的函数,如不说明定义域,则其定义域就是指使表达式有意义的一切实数组成的集合,称为函数的自然定义域.
例1 求函数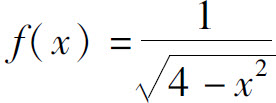 的定义域.
的定义域.
解 要使函数有意义,必须有
4-x2>0,
即
-2<x<2.
故函数的定义域为
D={x∣-2<x<2}.
函数的表示法主要有三种:解析法(或称公式法)、表格法和图形法.用图形法表示函数是基于函数图形的概念,称坐标平面上的点集
{(x,y)∣y=f(x),x∈D}
为函数y=f(x),x∈D的图形.
例2 函数
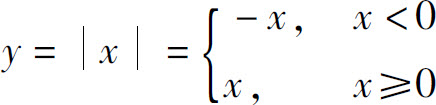
称为绝对值函数,它的定义域D=(-∞,+∞),它的图形如图1.2所示.
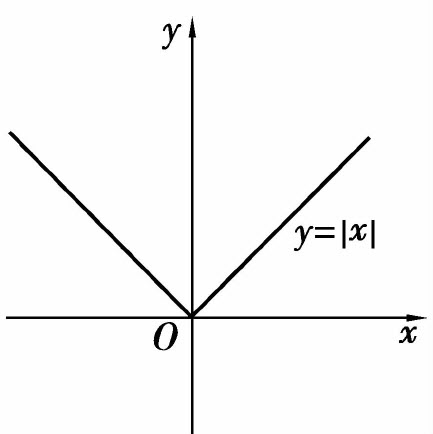
图1.2
例3 函数
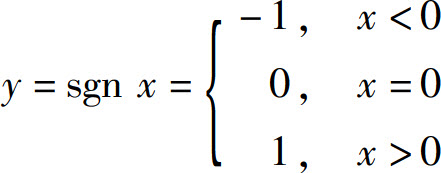
称为符号函数,它的定义域D=(-∞,+∞),它的图形如图1.3所示.
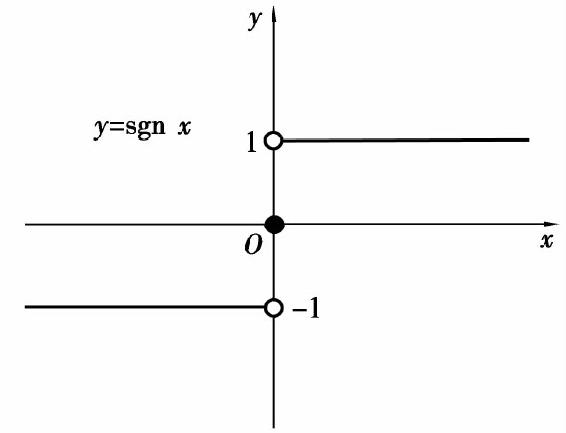
图1.3
例4 函数
y=[x]
称为取整函数.这里[x]表示不超过x的最大整数,称为x的整数部分.它的定义域D=(-∞,+∞),它的图形如图1.4所示.
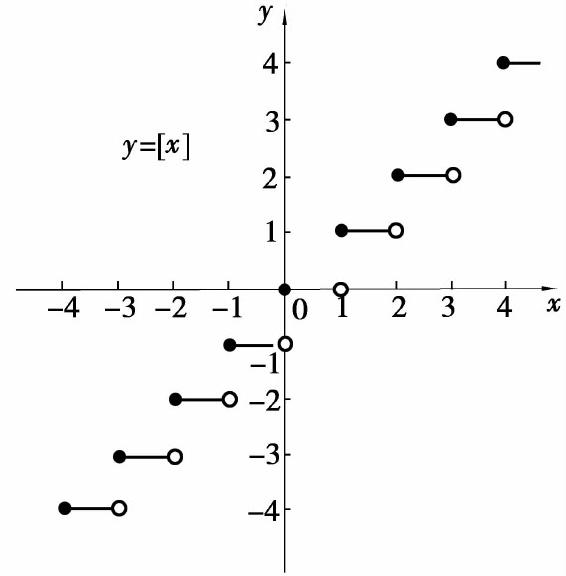
图1.4
上面几个函数在其定义域的不同区间,对应法则用不同的公式表达,这类函数称为分段函数.
分段函数在实际问题中也是经常出现的.例如,某市出租车按如下规定收费:当行驶里程不超过3 km时,一律收起步费10元;当行驶里程超过3 km时,除起步费外,对超过3 km且不超过10 km的部分,按2元/km计费,对超过10 km的部分,按3元/km计费.则车费C与行驶里程S之间的函数关系为
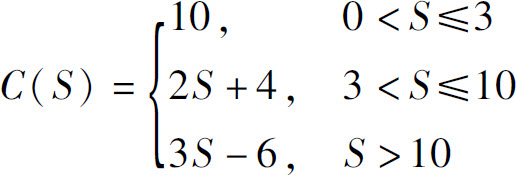
1.1.4 函数的性质
1)有界性
设函数f(x)在数集D上有定义.如果存在正数M,使对D中每一个x都有
∣f(x)∣≤M,
则称f(x)在D上有界,并称f(x)是D上的有界函数.否则称f(x)在D上无界.
直观上看,有界函数f(x)的图形介于水平线y=-M与y=M之间.
例如,正弦函数y=sin x和余弦函数y=cos x为(-∞,+∞)上的有界函数,因为对一切实数x有∣sin x≤1∣和∣cos x∣≤1.又如函数y=x3在[0,1]上是有界的,而在[0,+∞)上却是无界的.
2)单调性
设函数f(x)的定义域为D,区间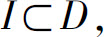 如果对任意的x1,x2∈I,当x1<x2时,有
如果对任意的x1,x2∈I,当x1<x2时,有
f(x1)<f(x2)(f(x1)>f(x2)),
则称f(x)在区间I上单调增加(单调减少),并称区间I为函数f(x)的单调增加区间(单调减少区间).
单调增加和单调减少的函数统称为单调函数.
函数在I上单调增加(单调减少),其图形沿x轴正向逐渐上升(逐渐下降).
例如函数y=x2在(-∞,+∞)内不具有单调性,但在(-∞,0]上单调减少,在[0,+∞)上单调增加,如图1.5所示.
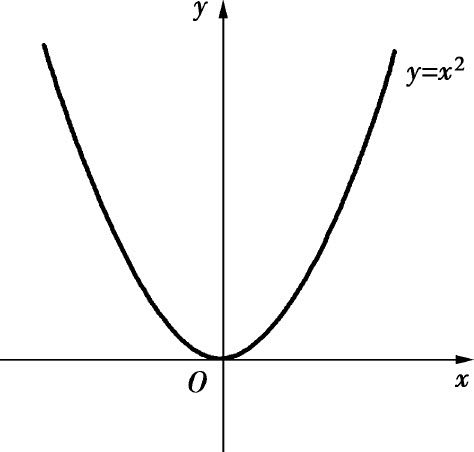
图1.5
3)奇偶性
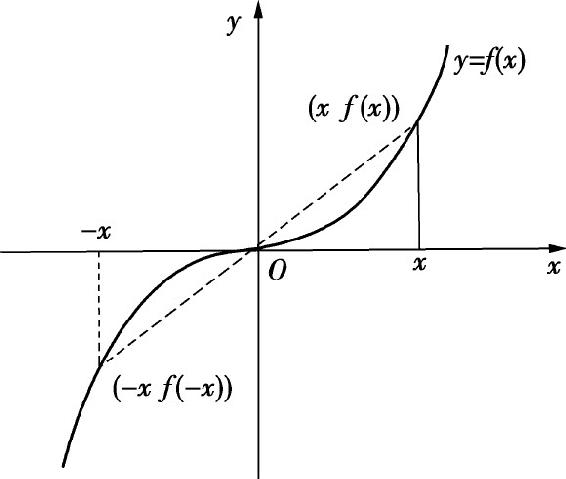
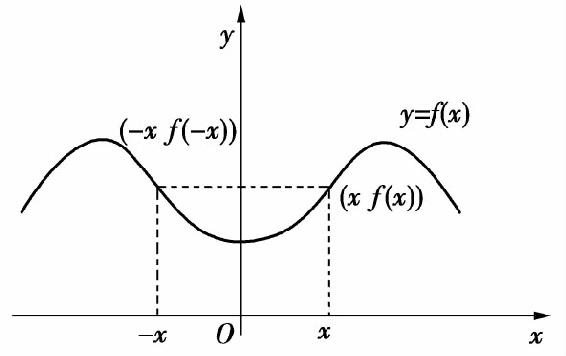
设函数f(x)的定义域D在数轴上关于原点对称.如果对任何x∈D有
f(-x)=-f(x),
则称f(x)是D上的奇函数;如果对任何x∈D有
f(-x)=f(x),
则称f(x)是D上的偶函数.
例如,f(x)=sin x是奇函数,因为f(-x)=sin(-x)=-sin x=-f(x).又例如,f(x)=cos x是偶函数,因为f(-x)=cos(-x)=cos x=f(x).
奇和偶的名称来自x的幂次.如果f(x)是x的奇数次幂,如f(x)=x或f(x)=x3,则它就是奇函数;如果f(x)是x的偶数次幂,如f(x)=x2或f(x)=x4,则它就是偶函数.
奇函数的图形关于原点对称,如图1.6所示;偶函数的图形关于y轴对称,如图1.7所示.
 |
 |
| 图1.6 | 图1.7 |
4)周期性
设函数f(x)定义域为D.如果存在正数T,使得对一切x∈D,都有x±T∈D,且
f(x+T)=f(x),
则称f(x)为D上的周期函数,称T为f(x)的一个周期.
显然,如果T为f(x)的周期,则对于任何正整数k,kT也是函数f(x)的周期.如果在周期函数的所有周期中有一个最小的,则称此周期为该函数的最小正周期.通常说周期函数的周期是指最小正周期.
例如,函数y=sin x,y=cos x都是周期为2π的周期函数.
1.1.5 反函数与复合函数
1)反函数的概念
设有函数y=f(x),x∈D,若对于每一个y∈f(D),有唯一的x∈D使得y=f(x),则在f(D)上定义了一个函数,记为
x=f-1(y),y∈f(D).
称这个函数为函数y=f(x)的反函数.
习惯上自变量用x表示,因变量用y表示,故函数y=f(x),x∈D的反函数记为
y=f-1(x),x∈f(D).
由反函数的定义可知,如果当x1≠x2时有f(x1)≠f(x2),则函数y=f(x)一定有反函数.由此可见,单调函数一定有反函数,并且其反函数有相同的单调性.
相对于反函数y=f-1(x)而言,原来的函数y=f(x)称为直接函数.如果将它们的图形画在同一坐标平面上,则这两个图形关于直线y=x对称,如图1.8所示.
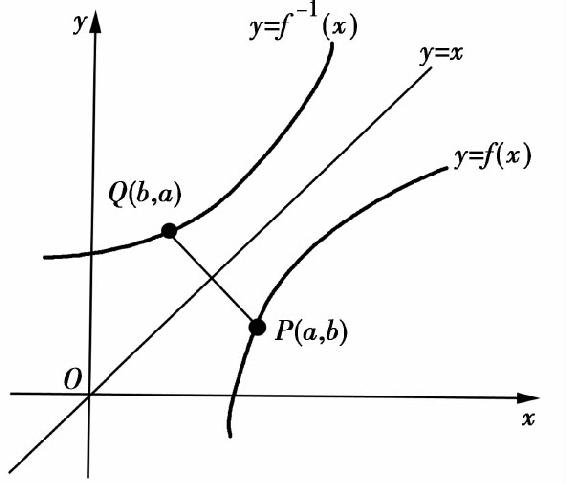
图1.8
例5 求函数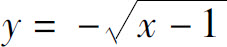 的反函数.
的反函数.
解 函数的定义域为x∈[1,+∞),值域为(-∞,0],由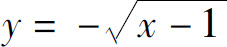 解得
解得
x=y2+1.
所求反函数为
y=x2+1,x∈(-∞,0].
例6 反正弦函数y=arcsin x是y=sin x,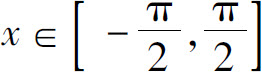 的反函数,其定义域为[-1,1],值域为
的反函数,其定义域为[-1,1],值域为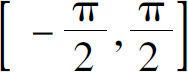 如图1.9(a)所示.
如图1.9(a)所示.
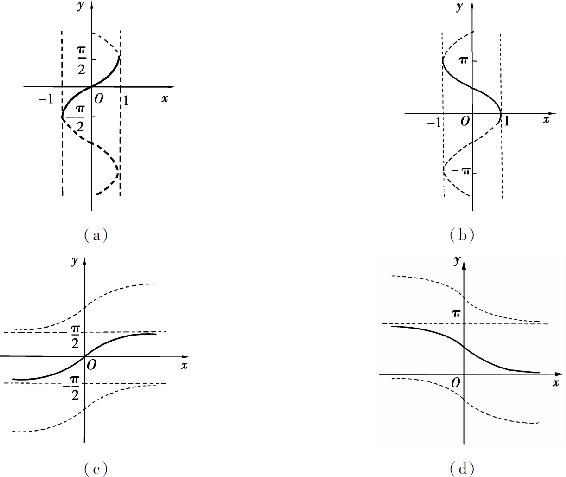
图1.9
反余弦函数y=arccos x是y=cos x,x∈[0,π]的反函数,其定义域为[-1,1],值域为[0,π],如图1.9(b)所示.
反正切函数y=arctan x是y=tan x,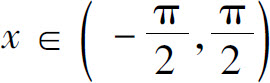 的反函数,其定义域为(-∞,+∞),值域为
的反函数,其定义域为(-∞,+∞),值域为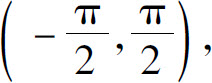 如图1.9(c)所示.
如图1.9(c)所示.
反余切函数y=arccot x是y=cot x,x∈(0,π)的反函数,其定义域为(-∞,+∞),值域为(0,π),如图1.9(d)所示.
2)复合函数的概念
将函数u=g(x)代入另一个函数y=f(u)的自变量的位置,得到的新函数y=f[g(x)]称为函数y=f(u)和函数u=g(x)的复合函数.复合函数的定义域是使得f[g(x)]有意义的x组成的集合.其中,f称为外(层)函数,g称为内(层)函数,u称为中间变量.
例如,函数y=f(u)=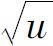 与函数u=g(x)=1-x2的复合函数为
与函数u=g(x)=1-x2的复合函数为
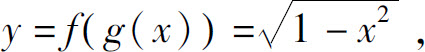
其定义域为[-1,1].
并不是任意两个函数都能进行复合.例如y=arcsin u与u=2+x2就不能进行复合,因为对任意实数x,表达式arcsin(2+x2)没有意义.
复合函数也可由多个函数相继复合而成.例如,由三个函数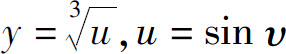 与υ=x2相继复合而成的复合函数为
与υ=x2相继复合而成的复合函数为
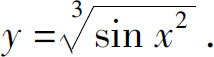
1.1.6 初等函数
下列函数称为基本初等函数.
常量函数:y=C(C是常数).
幂函数:y=xα(α为实数).
指数函数:y=ax(a>0,a≠1).
对数函数:y=logax(a>0,a≠1).
三角函数:y=sin x,y=cos x,y=tan x,y=cot x.
反三角函数:y=arcsin x,y=arccos x,y=arctan x,y=arccot x.
由基本初等函数经过有限次四则运算与复合运算形成的并可以由一个式子表示的函数,称为初等函数.
例如,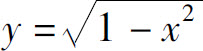 是多项式u=1-x2与幂函数
是多项式u=1-x2与幂函数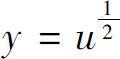 复合而成,而多项式1-x2又是常数1与幂函数x2之差,所以
复合而成,而多项式1-x2又是常数1与幂函数x2之差,所以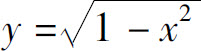 是初等函数.
是初等函数.
又如符号函数、取整函数不是初等函数.
分段函数常常不是初等函数,但有些分段函数却是初等函数.如函数
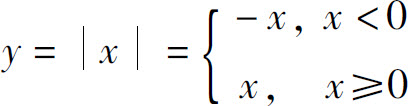
是一个分段函数,因为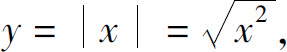 所以是初等函数.
所以是初等函数.
习题1.1
1.求下列函数的定义域:
(1)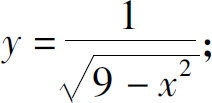
(2)y=ln(x+1)
(3)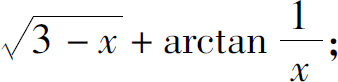
(4)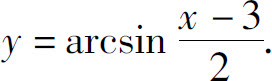
2.设函数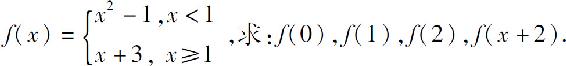
3.判断下列函数的奇偶性:
(1)y=x+sin x;
(2)y=|sin x |;
(3)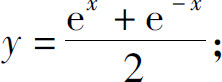
(4)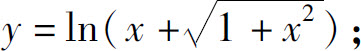
(5)y=sin x - cos x+1;
(6)y=x(x-1)(x+1).
4.证明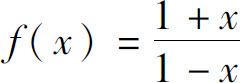 在(-∞,1)与(1,+∞)内单调增加.能否说f(x)在(-∞,1)∪(1,+∞)内单调增加?
在(-∞,1)与(1,+∞)内单调增加.能否说f(x)在(-∞,1)∪(1,+∞)内单调增加?
5.求下列函数的反函数:
(1)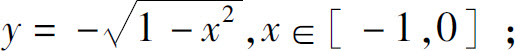
(2)y=1+ln(x+3);
(3)y=e4x+5;
(4)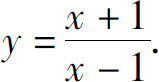
6.指出下列函数是由哪些基本初等函数复合而成:
(1)y=(1+x)20;
(2)y=(arcsin x2)2;
(3)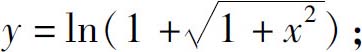
(4)