8.5 泰勒级数
8.5 泰勒级数
上一节讨论了幂级数的收敛域及其和函数.本节讨论相反的问题,即将一个函数f(x)表示成一个幂级数.
8.5.1 泰勒级数
假设f(x)是收敛区间为I的幂级数的和函数,即
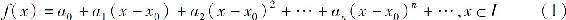
在区间I内重复逐项求导,得
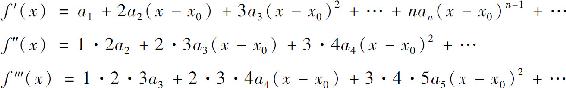
第n阶导数
f(n)(x)=n!an+(带因式(x-x0)的项的和)
…
因为这些等式在x=x0时成立,故有
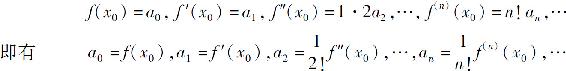
这些公式揭示了区间I上收敛于f(x)的幂级数(1)的系数与f(x)的关系.如果存在这样一个级数,则这个级数必定是
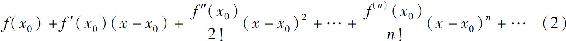
定义1 设函数f(x)在含有x0的某个开区间I内具有任意阶的导数,则级数
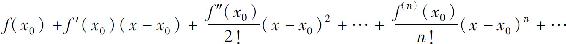
称为f(x)在x0处的泰勒级数.
特别地,f(x)在x=0处泰勒级数
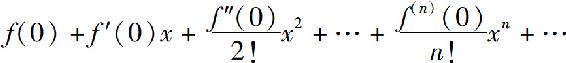
称为f(x)的麦克劳林级数.
必须注意的是,只要函数f(x)在点x0具有任意阶导数,则可以形式地写出它的泰勒级数(2).但泰勒级数是否收敛?如果收敛,是否收敛于函数f(x)?
8.5.2 泰勒公式
不论是在近似计算还是在理论分析中,对于一些较复杂的函数,往往希望用一些较简单的函数来近似表达.由于多项式函数只要对自变量进行有限次的加、减、乘三种运算就能求出它的函数值,因此经常用多项式来近似表达函数.
由函数微分的定义,如果函数f(x)在点x0处可导,则有
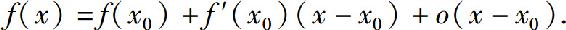
即在点x0附近,f(x)可用一次多项式
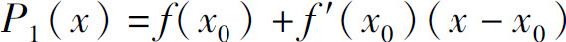
来逼近,其误差为o(x-x0).
如果f(x)在点x0处有更高阶的导数,就可用更高阶的多项式来逼近.
定义2 设函数f(x)在含有x0的某个开区间I内具有直到n阶的导数,则
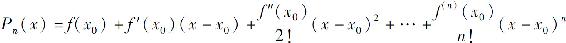
称为f(x)在x0处的n阶泰勒多项式.
例1 求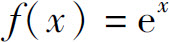 在x=0处的泰勒级数和n阶泰勒多项式.
在x=0处的泰勒级数和n阶泰勒多项式.
解 因为
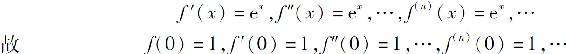
从而ex在x=0处的泰勒级数为
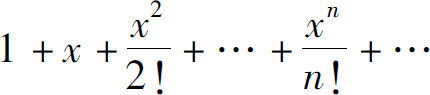
在x=0处的n阶泰勒多项式为
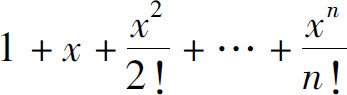
如果在x=0附近用泰勒多项式来近似代替ex,则随着阶数的增加,它们就越来越接近于ex,如图8.3所示.
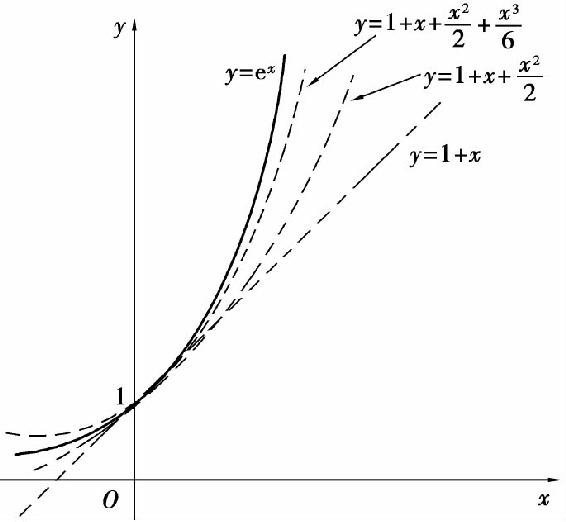
图8.3
用函数f(x)的泰勒多项式来逼近f(x)的精确程度如何?下面的定理提供了一个估计的途径.
定理1(泰勒定理) 如果函数f(x)在含有x0的某个开区间I内具有直到n+1阶的导数,则对任意x∈I,有
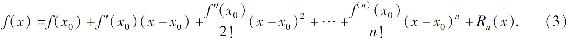
其中
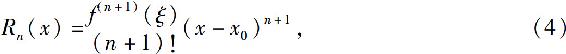
这里ξ是x0与x之间的某个值.
证 设Rn(x)=f(x)-pn(x),只需证明
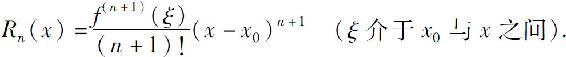
由假设可知,Rn(x)在I内具有直到(n+1)阶的导数,且
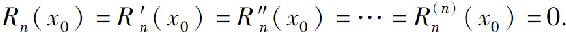
对函数Rn(x)和(x-x0)n+1在以x0及x为端点的区间上应用柯西中值定理(显然,这两个函数满足柯西中值定理的条件),得
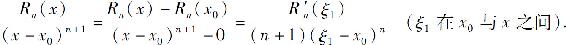
再对函数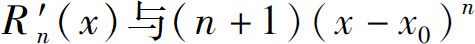 与(n+1)(x-x0)n在以x0及ξ1为端点的区间上应用柯西中值定理,得
与(n+1)(x-x0)n在以x0及ξ1为端点的区间上应用柯西中值定理,得
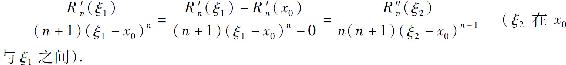
如此继续,(n+1)次应用柯西中值定理,得
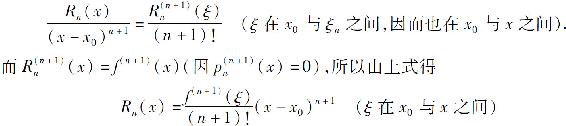
公式(3)称为f(x)按(x-x0)的幂展开的n阶泰勒公式,而Rn(x)的表达式(4)称为拉格朗日型余项.
当n=0时,泰勒公式变成拉格朗日中值公式:
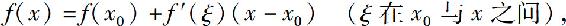
所以泰勒定理是拉格朗日中值定理的推广.
由泰勒定理可知,以多项式Pn(x)近似表达函数f(x)时,其误差为|Rn(x)|.如果在区间I内|f(n+1)(x)|≤M,则
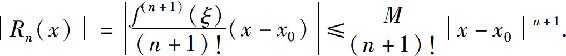
可见,当x→x0时Rn(x)是比(x-x0)n高阶的无穷小.
在不需要余项的精确表达式时,n阶泰勒公式也可写成
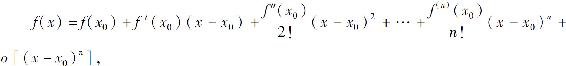
这里Rn(x)=o[(x-x0)n]称为皮亚诺型余项.
在泰勒公式中令x0=0,则
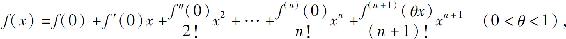
或写成
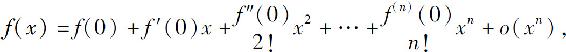
称为麦克劳林公式.
8.5.3 函数展开成幂级数
现在,来回答8.5.1提出的问题.
因为f(x)的泰勒多项式Pn(x)是其泰勒级数(2)前n+1项部分和sn+1(x),故由
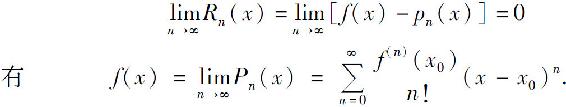
所以,如果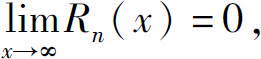 则f(x)在x0处的泰勒级数收敛于f(x).反之亦然.
则f(x)在x0处的泰勒级数收敛于f(x).反之亦然.
定理2 如果函数f(x)在含有x0的某个开区间I内具有任意阶导数,则在I内f(x)在点x0处的泰勒级数收敛于f(x)的充分必要条件是:
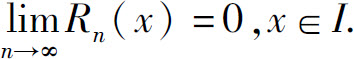
定义 如果在含有x0的某个开区间I内函数f(x)的泰勒级数收敛于f(x),即
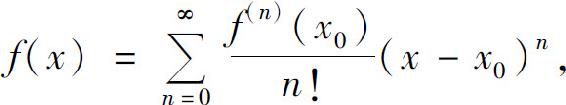
则称f(x)在I内可展开成泰勒级数.
把f(x)展开成x的幂级数的具体步骤如下:
(1)求出f(x)的各阶导数;
(2)求函数及其各阶导数在x=0的值;
(3)写出幂级数
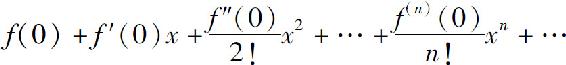
并求出收敛半径R.
(4)考察当x∈(-R,R)时
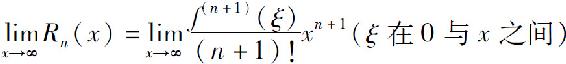
是否为零.
如果为零,则函数f(x)在区间(-R,R)内的幂级数展开式为
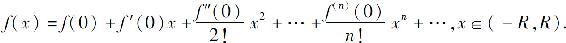
例2 将f(x)=ex展开成x的幂级数.
解 由例1,ex的麦克劳林级数为
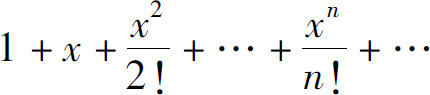
其收敛半径R=+∞.
对于任意确定的数x,拉格朗日型余项的绝对值
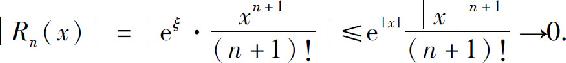
这是因为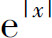 是一个有限数,而
是一个有限数,而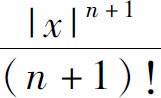 为正项收敛级数
为正项收敛级数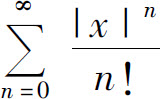 的通项,由级数收敛的必要条件,对(-∞,+∞)上的一切x有
的通项,由级数收敛的必要条件,对(-∞,+∞)上的一切x有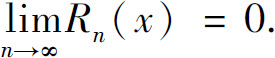 所以得展开式
所以得展开式
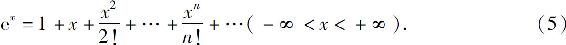
例3 将f(x)=sin x展开成x的幂级数.
解 因为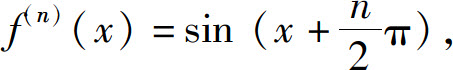 从而
从而
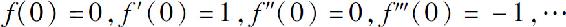
f(n)(0)依次循环地取0,1,0,-1.于是函数的麦克劳林级数为
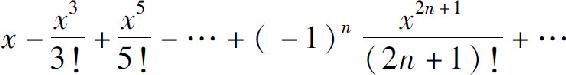
其收敛半径R=+∞.
对任何固定的数x,余项的绝对值
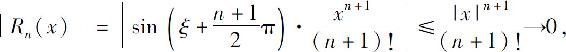
于是得展开式
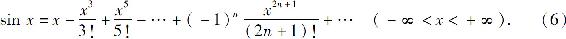
例4 将函数f(x)=(1+x)m展开成x的幂级数,其中m为任意常数。
解 f(x)的各阶导数为
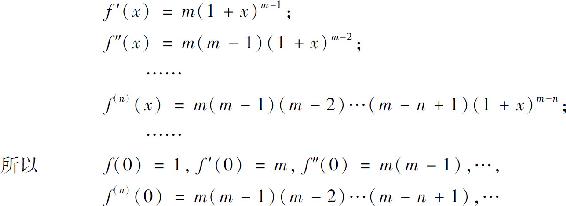
于是得幂级数
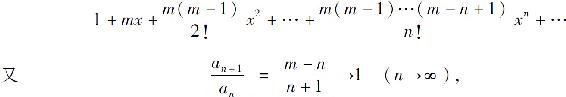
所以级数的收敛区间为(-1,1).
可以证明,当x∈(-1,1)时,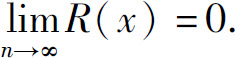 于是得展开式
于是得展开式
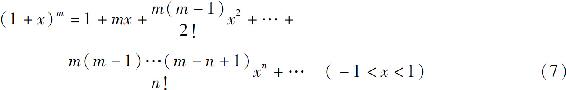
公式(7)称为二项展开式.当m为正整数时,级数只有m+1项
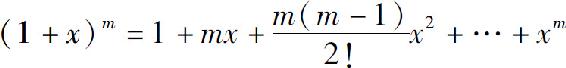
正是代数学中的二项式定理.
当m不是正整数或零时,级数是无限的.
当m=-1时,即可得下面熟悉的几何级数的求和公式
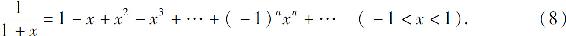
当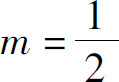 时,二项展开式为
时,二项展开式为
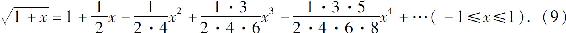
对于大多数函数而言,通过求导计算泰勒级数的系数很烦琐,并且分析余项是否趋于零也不是容易的事情.因此,常利用已知的幂级数展开式、幂级数和函数的运算性质以及变量代换等来求函数的幂级数展开式.我们称这种方法为间接展开法.
例5 将函数cos x展开成x的幂级数.
解 对展开式(6)逐项求导,得
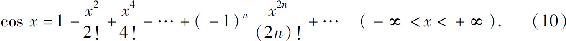
需要说明的是,假定函数f(x)在开区间(-R,R)内的展开式为
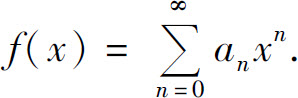
如果函数f(x)在该区间的端点x=R(或x=-R)处连续,上式右边的幂级数在x=R(或x=-R)仍收敛,则根据幂级数和函数的连续性,该展开式对x=R(或x=-R)也成立.
例6 将函数f(x)=ln(1+x)展开成x的幂级数.
解 注意到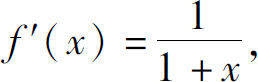 而
而
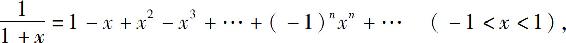
所以将上式两边从0到x逐项积分,得
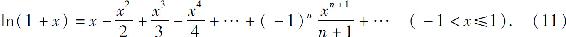
展开式对x=1也成立,因为上式右边的幂级数当x=1时收敛,且ln(1+x)在x=1处连续.
例7 将函数lnx展开成(x-2)的幂级数.
解 由式(11),得
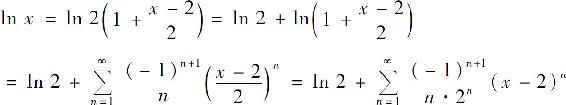
当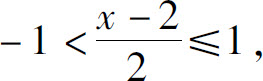 即0<x≤4时成立.
即0<x≤4时成立.
例8 将函数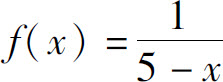 展开成(x-2)的幂级数.
展开成(x-2)的幂级数.
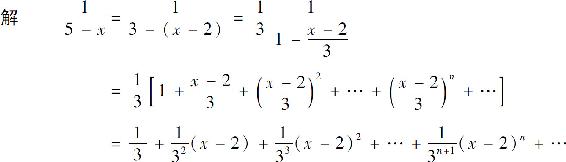
当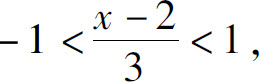 即-1<x<5时成立.
即-1<x<5时成立.
习题8.5
1.求下列函数在点x0处的2阶和3阶泰勒多项式:
(1)lnx,x0=1;
(2)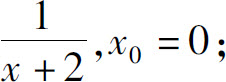
(3)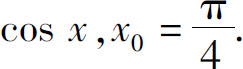
2.将下列函数展开成x的幂级数:
(1)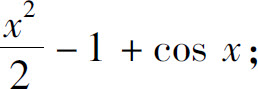
(2)x2 sin x;
(3)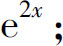
(4)ln(a+x)(a>0);
(5)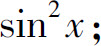
(6)(1+x)ln(1+x).
3.将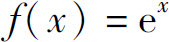 展开成(x-1)的幂级数.
展开成(x-1)的幂级数.
4.将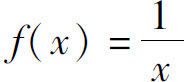 展开成(x-a)(a>0)的幂级数.
展开成(x-a)(a>0)的幂级数.
5.设在开区间(-c,c)内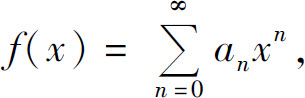 证明
证明
(1)如果f(x)为奇函数,则a0=a2=a4=…=0,即f(x)的级数只含奇次幂;
(2)如果f(x)为偶函数,则a1=a3=a5=…=0,即f(x)的级数只含偶次幂.
