1.2　数列极限

1.2　数列极限

1.2.1　数列极限的定义

定义1　如果按照某一法则，对每个n∈Z＋，都对应着一个确定的实数an，这些实数按下标n从小到大排列得到的一个序列：

a1，a2，…，an，…

称为无穷数列，简称为数列，简记为an．其中，an称为数列的通项或一般项．

显然，数列可以理解为定义域为正整数集Z＋的函数：

an＝f（n），n∈Z＋．

例如

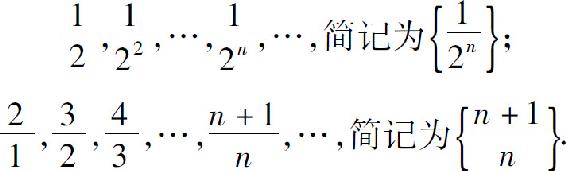
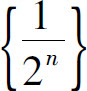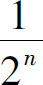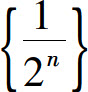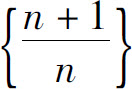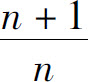不难看出，数列的通项随着n的增大而无限接近于0，称0为数列的极限；数列的通项随着n的增大而无限接近于1，称1为数列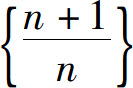的极限．

一般地，对于数列｛an｝，如果当n无限增大时，an无限地接近某一个常数a，则称此数列为收敛数列，常数a称为它的极限．

为了进一步理解“无限接近”的意义，这里进一步考察数列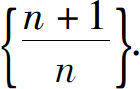

注意到实数a，b的接近程度由|a－b|确定，|a－b|越小，则a，b越接近．因此，要说明“数列通项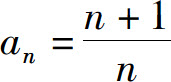随着n的增大而无限地接近于1”，只要说明“当n充分大以后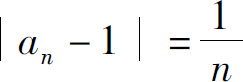，可以小于预先给定的任意小的正数．”

事实上，要使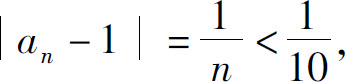只要n＞10即可，即从第11项起的一切项an与1之差的绝对值都小于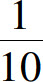；要使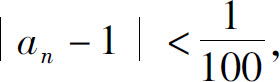只要n＞100即可．一般地，任意给定ε＞0，不论它多么小，要使|an－1|＜ε，只要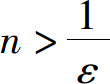即可，也就是从第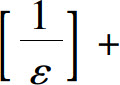1项起的一切项都满足∣an－1∣＜ε．因为ε＞0是任意的，这就说明an可以无限地接近于1．

定义2　设｛an｝是一数列，a为定数．如果对任意给定的正数ε，总存在正整数N，使得当n＞N时，有

∣an－a∣＜ε，

则称a为数列｛an｝的极限，或称数列｛an｝收敛于a，记为

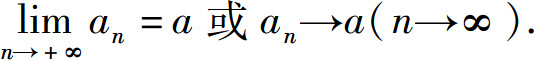
如果数列｛an｝没有极限，则称｛an｝为发散数列．

这个定义被称为数列极限的ε-N定义．为书写简便，定义可简述为：

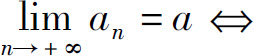对ᗄε＞0，ƎN＞0，当n＞N时，有∣an－a∣＜ε．

其中，符号“ᗄ”表示“任意给定”，符号“Ǝ”表示“存在”．

需要注意的是，定义中的ε是可以任意给定的正数．ε越小，表示an与定数a越接近，从而ε的任意性保证了an可以无限地接近于a；一旦ε给定后，ε就是一个确定的正数，从而由∣an－a∣＜ε可找到相应的N，但N不是由ε所唯一确定的．

例1　证明：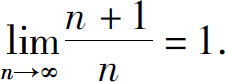

证　对任意ε＞0，要使

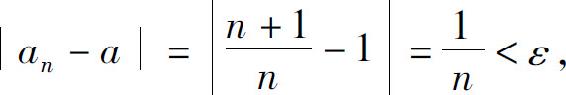
只需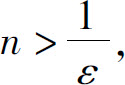故可取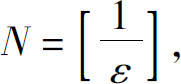则当n＞N时就有

∣an－a∣＜ε，

故

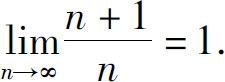
例2　证明：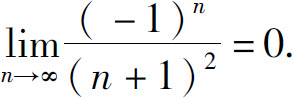

证　因为

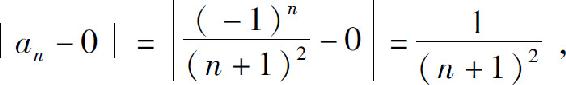
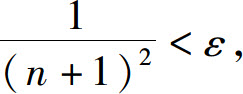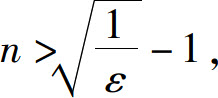故对任意给定的ε＞0（不妨设ε＜1），要使∣an－0∣＜ε，只需即因此可取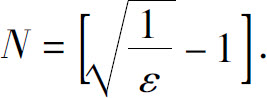则当n＞N时，就有

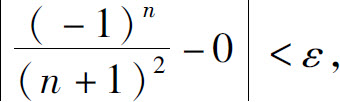
故

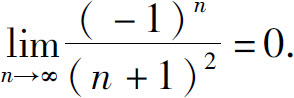
1.2.2　收敛数列的性质

性质1（唯一性）　若数列｛an｝收敛，则它的极限是唯一的．

定义3　对于数列｛an｝，如果存在正数M，使得对一切的正整数n，有

∣an∣≤M，

则称数列｛an｝是有界的；否则，就称数列｛an｝是无界的．

性质2（有界性）　若数列｛an｝收敛，则an必有界．

证　设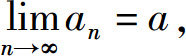取ε＝1，则存在正整数N，对一切n＞N有

∣an－a∣＜1．

于是，当n＞N时

∣an∣＝∣（an－a）＋a∣≤∣an－a∣＋∣a∣＜1＋∣a∣．

取M＝max{∣a1∣，∣a2∣，…，∣aN∣，1＋∣a∣}，则对一切正整数n，都有

∣an∣＜M，

即{an}有界．

有界只是数列收敛的必要条件，而非充分条件，即有界数列不一定收敛．例如数列{（－1）n}有界，但它并不收敛．

性质3（保号性）　若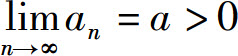（或a＜0），则存在正整数N，使得当n＞N时有an＞0（或an＜0）．

证　设a＞0．取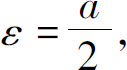因为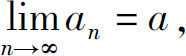故存在正整数N，使得当n＞N时，有

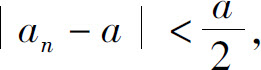
从而

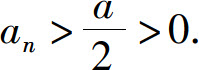
性质3表明：若数列的极限为正（或负），则该数列从某一项开始以后所有项也为正（或负）．

在数列{an}中任意抽取无限多项并保持这些项在原数列{an}中的先后次序，这样得到的一个数列称为数列{an}的子数列．

性质4　如果数列{an}收敛于a，那么它的任一子数列也收敛于a．

1.2.3　数列极限的运算法则

定理1　如果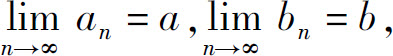则

（1）

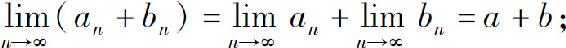
（2）

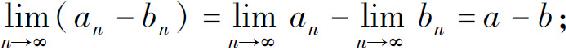
（3）

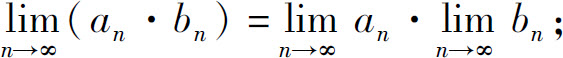
（4）

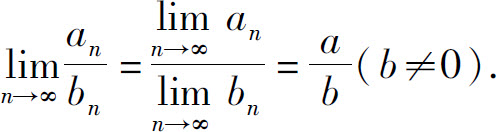
例3　求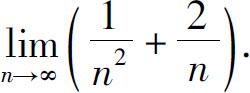

解　因为

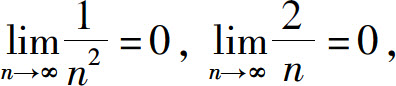
所以

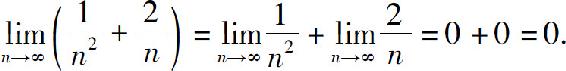
例4　求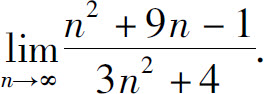

解　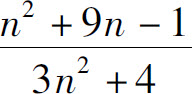的分子和分母同除以n2后，再用极限运算法则得

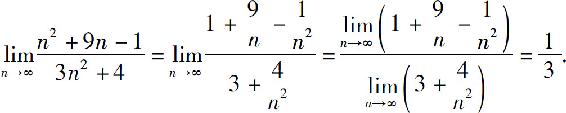
例5　求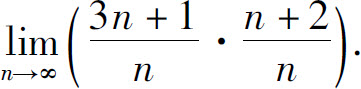

解

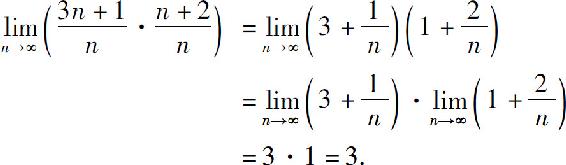
习题1.2

1．按ε-N定义证明：

（1）

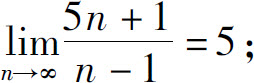
（2）

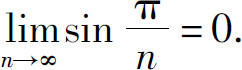
2．求下列极限：

（1）

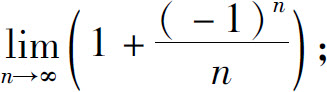
（2）

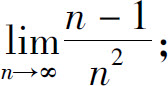
（3）

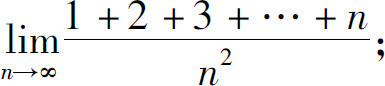
（4）

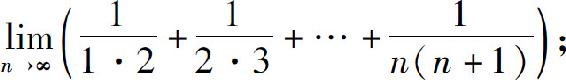
（5）

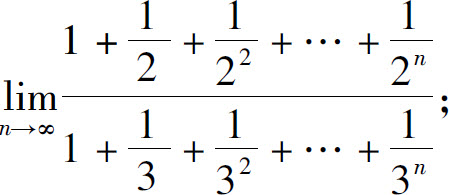
（6）

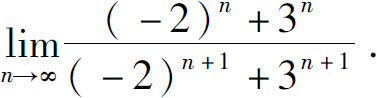
3．设{an}是收敛数列，{bn}是发散数列，证明{an＋bn}是发散数列．又问{anbn}是否必为发散数列？