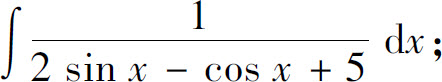4.4　有理函数的积分

4.4　有理函数的积分

4.4.1　有理函数的积分

设Pn（x）和Qm（x）分别是n次和m次多项式，则称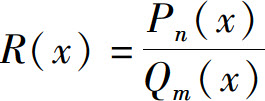为有理函数或有理分式．当n＜m时，称这有理函数为真分式；而当n≥m时，称这有理函数为假分式．

利用多项式的除法，总可以把一个假分式化为一个多项式与一个真分式之和．例如

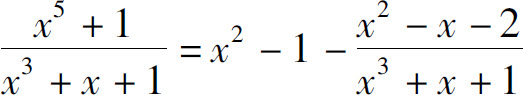
多项式的不定积分容易计算，因此我们只需讨论有理真分式的不定积分问题．

对于真分式，可以将其分解为最简分式之和．所谓最简分式是指形如

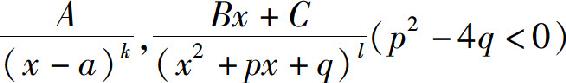
的分式，其中k，l为正整数．

分式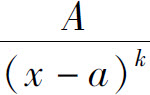的不定积分容易计算，下面举例说明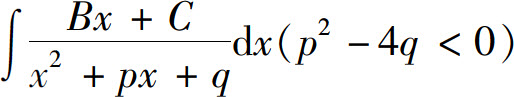的计算方法．

例1　求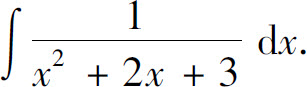

解

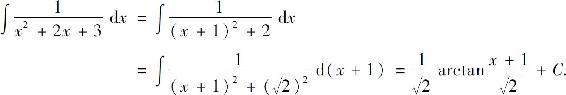
例2　求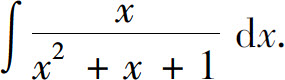

解　将分子一部分凑成分母的导数．

如何将真分式分解为最简分式？有下述代数理论：

设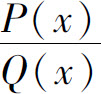为真分式，如果分母可分解为

Q（x）＝（x－a）kQ1（x），

其中Q1（x）不含因式（x－a），则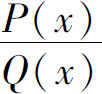的分解式中应包含

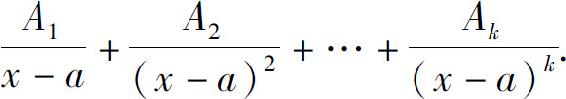
其中A1，A2，…，Ak为待定系数．如果分母可分解为

Q（x）＝（x＋px＋q）lQ2（x）（p2－4q＜0），

其中Q2（x）不含因式（x2＋px＋q），则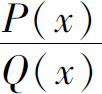的分解式中应包含

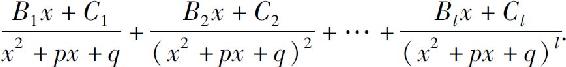
其中B1，B2，…，Bl，C1，C2，…，Cl为待定系数．

例3　求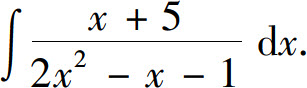

解　因为

2x2－x－1＝（2x＋1）（x－1），

故可设

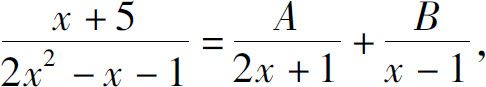
其中A，B是待定的常数．两端去分母后，得

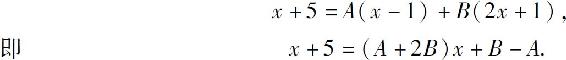
比较上式两端x的系数及常数项，得方程组：

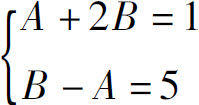
解得A＝－3，B＝2，因此

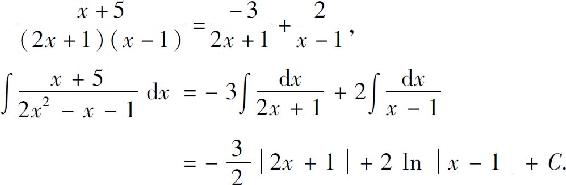
例中也可通过赋予x的特殊值求得A，B：令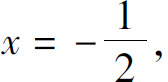得A＝－3；令x＝1，得B＝2．

例4　求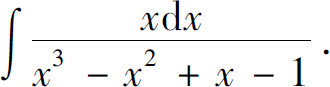

解　分母可分解为

x3－x2＋x－1＝（x－1）（x2＋1），

故可设

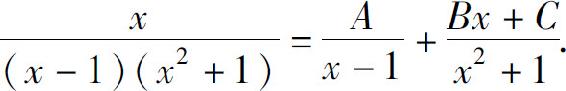
两端去分母后，得

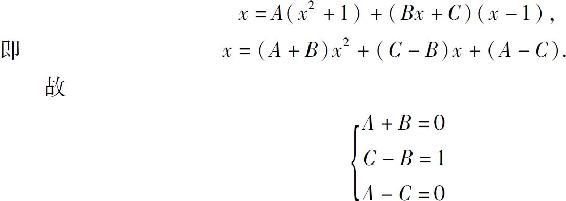
解得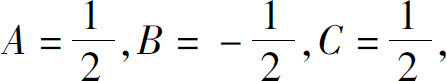因此

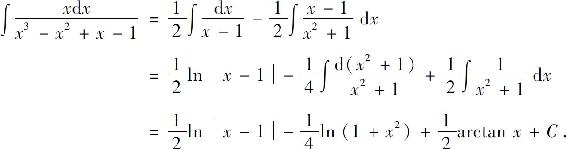
例5　求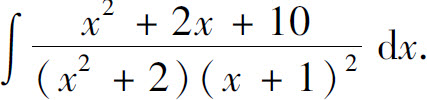

解设

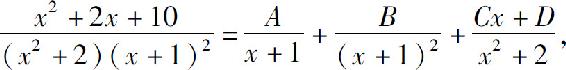
两端去分母后，得

x2＋2x＋10＝（A＋C）x3＋（A＋B＋C＋2D）x2＋（2A＋C＋2D）x＋2A＋2B＋D．

故

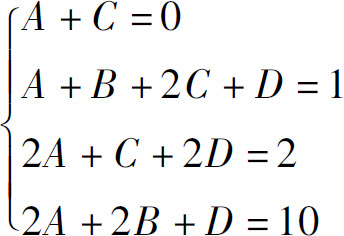
解得A＝0，B＝3，C＝－2，D＝0，所以

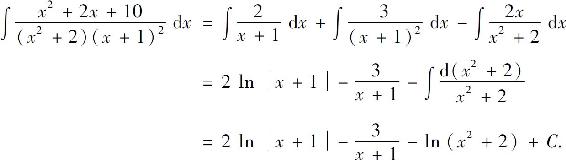
4.4.2　三角函数有理式的积分

三角函数有理式是由三角函数和常数经过有限次四则运算构成的函数，例如

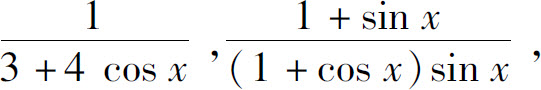
其积分通常记为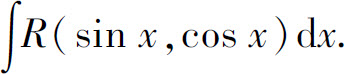

对积分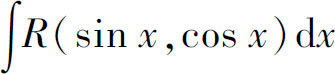，可通过变换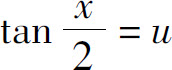化为关于u的有理函数的积分．因为

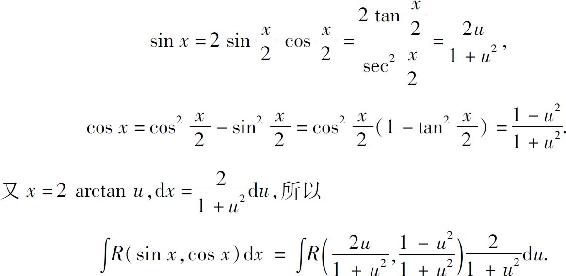
这是关于u的有理函数的积分．

例6　求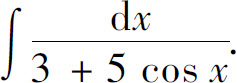

解　令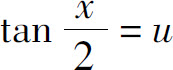则

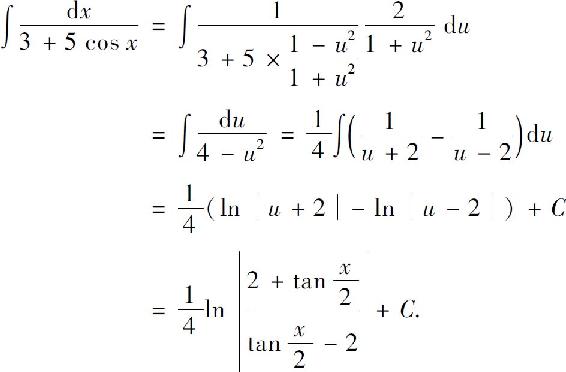
虽然变量代换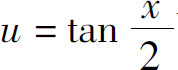可将三角函数有理式的积分转化为有理函数的积分，但某些三角函数有理式的不定积分用其他方法可能更为简便．

例7　求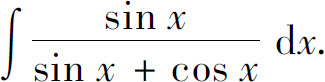

解

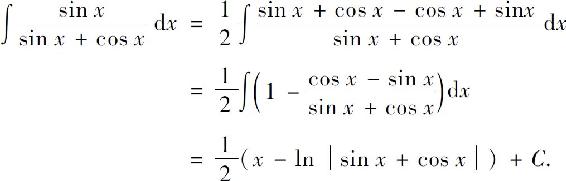
到此为止，我们已经讨论了求不定积分的几种基本方法及求某些类型函数不定积分的方法．什么叫做“求”一个积分呢？回顾前面的讨论，所谓“求”一个积分，其实是说要用初等函数把这个积分表示出来．在这种意义下，不是所有的初等函数的积分都可以求出来的．例如下列不定积分

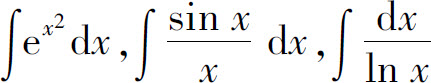
虽然存在，但它们都是求不出来的，即不能用初等函数来表示．

习题4.4

求下列不定积分：

1．

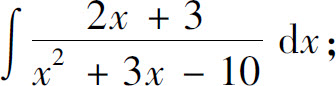
2．

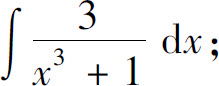
3．

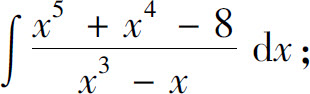
4．

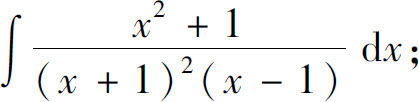
5．

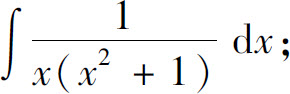
6．

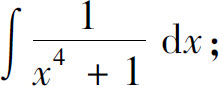
7．

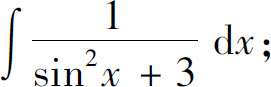
8．

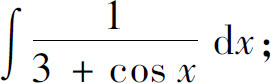
9．

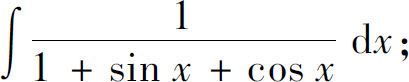
10．