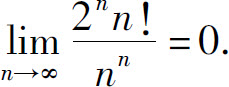8.2 正项级数
8.2 正项级数
给定一个级数，我们有两个问题：
（1）级数是否收敛？
（2）如果级数收敛，它的和是多少？
就第一个问题，本节研究没有负项的级数，即正项级数．
设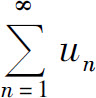
是一个正项级数，其部分和为sn，则有
s1≤s2≤…≤sn≤…
即部分和数列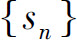
是一个单调增加数列．根据单调有界准则，如果数列
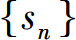有界，则其极限一定存在，从而正项级数
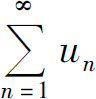收敛；反过来，如果正项级数
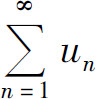收敛，即数列
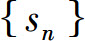有极限，故数列
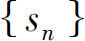有界．
定理1 正项级数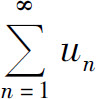
收敛的充分必要条件是它的部分和数列有界．
由此可得正项级数收敛性的一个基本判别法．
定理2（比较判别法） 设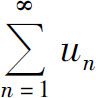
是正项级数．
（1）如果存在一个收敛的正项级数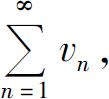
有un≤vn，则
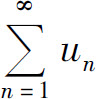收敛；
（2）如果存在一个发散的正项级数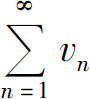
，有un≥vn，则
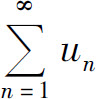发散．
证 （1）设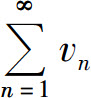
收敛于σ，则
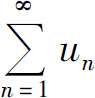的部分和
sn＝u1＋u2＋…＋un≤v1＋v2＋…＋vn≤σ，
即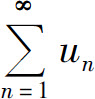
的部分和数列
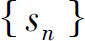有界，从而由定理1知级数收敛．
（2）用反证法．假设级数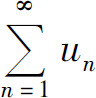
收敛，由（1）可知级数
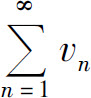收敛，这与定理所给条件矛盾，所以
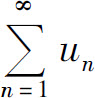发散．
因为级数的收敛性与级数前有限项无关，我们可得如下推论：
推论 设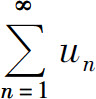
是正项级数．
（1）如果存在一个收敛的正项级数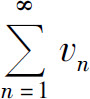
和正整数N，使得当n＞N时，有un≤kvn（k＞0），则
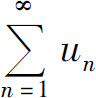收敛；
（2）如果存在一个发散的正项级数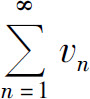
和正整数N，使得当n＞N时，有un≥kvn（k＞0），则
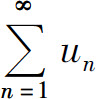发散．
例1 讨论p级数
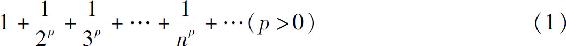
的收敛性．
解 当p≤1时，有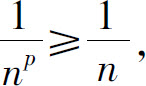
由于调和级数
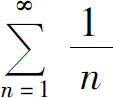是发散的，故级数（1）发散．
当p＞1时，因为对任意x≥1，当k－1≤x≤k时，有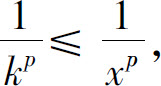
所以
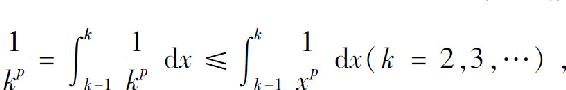
从而级数（1）的部分和
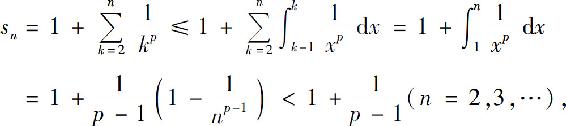
故部分和数列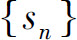
有界，所以级数（1）收敛．
综上所述，当p≤1时，p级数发散；当p＞1时，p级数收敛．
例如，级数
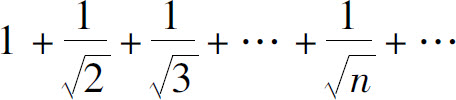
是p级数，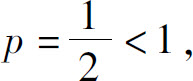
因而级数是发散的．而p级数
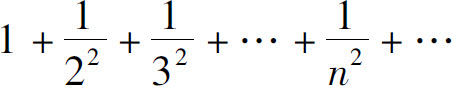
是收敛的，因为p＝2＞1．
例2 讨论级数
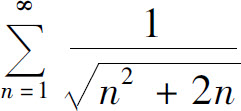
的收敛性．
解 因为n2＋2n＜n2＋2n＋1＝（n＋1）2，所以
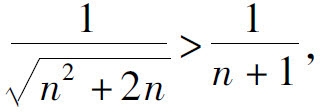
而级数
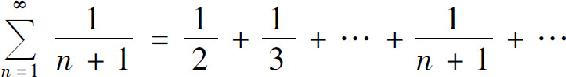
是发散的，由比较判别法知原级数也是发散的．
在应用上，我们常使用较为方便的比较判别法的极限形式．
定理3（比较判别法的极限形式） 设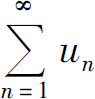
和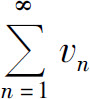
都是正项级数，且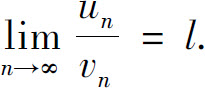
（1）如果0＜l＜＋∞，则级数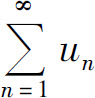
和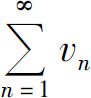
同时收敛或同时发散；
（2）如果l＝0，并且级数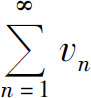
收敛，则级数
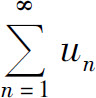收敛；
（3）如果l＝∞，并且级数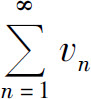
发散，则级数
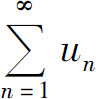发散．
例3 判定级数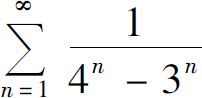
的收敛性．
解 由于一般项
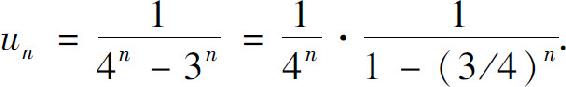
令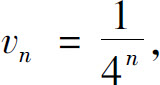
则
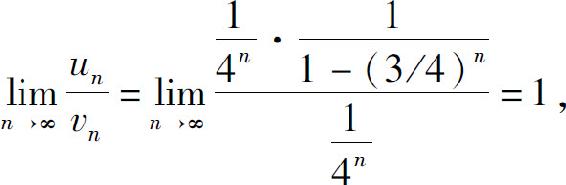
而几何级数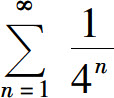
收敛，所以级数
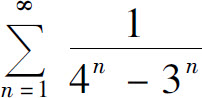收敛．
例4 判定级数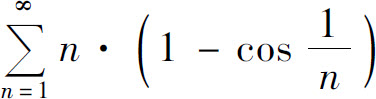
的收敛性．
解 当n→∞时，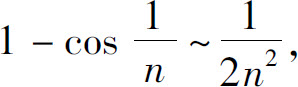
故
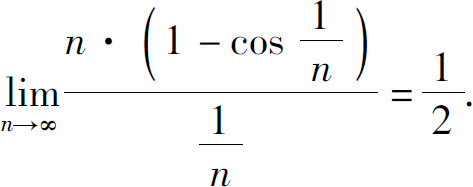
而调和级数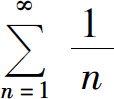
发散，故级数
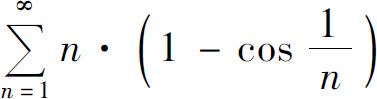发散．
应用比较判别法时，需要找到一个已知收敛性的级数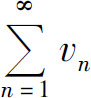
作为比较的对象，最常选用的是几何级数和p级数．但在不少情况下要找到这类比较对象是困难的，为此，下面介绍更简单直观的比值判别法．这种方法不需借助其他的级数，因此使用起来更为简便．比值判别法通过考察通项的比值
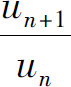来测量级数增长的速率．对于几何级数
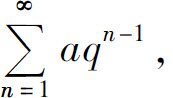这个速率是一个常数
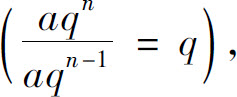当且仅当这个速率的绝对值小于1时级数收敛．比值判别法将这个结果推广为通用的规则．
定理4（比值判别法） 设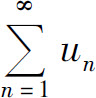
为正项级数，如果
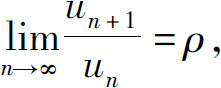
则 （1）当ρ＜1时，级数收敛；
（2）当ρ＞1（或ρ＝∞）时，级数发散；
（3）当ρ＝1时，级数可能收敛也可能发散．
证 （1）当ρ＜1时．取一个适当的正数ε，使得ρ＋ε＝r＜1，根据极限的定义，存在正整数N，当n＞N时有
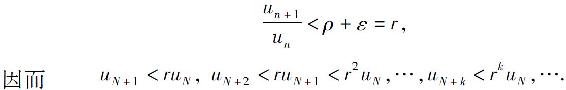
而级数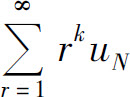
收敛（公比r＜1的几何级数），于是由比较判别法可知级数
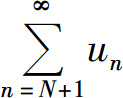也收敛，从而级数
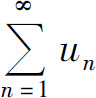收敛．
（2）当ρ＞1时．因为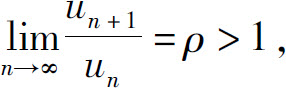
所以存在正整数N，当n＞N时有
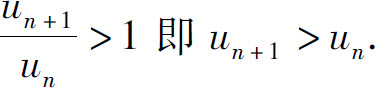
由此可见，从第N项以后un是递增的，从而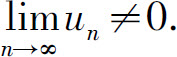
根据级数收敛的必要条件知级数
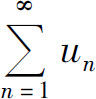发散．
类似可证，当ρ＝∞时，级数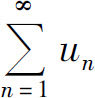
发散．
（3）当ρ＝1时，级数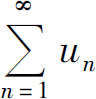
可能收敛也可能发散．例如p级数
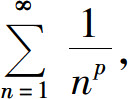对任意的p＞0都有
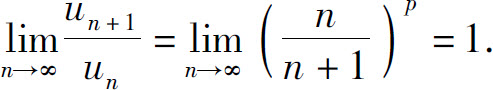
但我们知道，当p≤1时级数发散，当p＞1时级数收敛．
例5 讨论级数
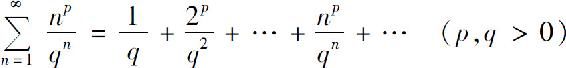
的收敛性．
解 因为
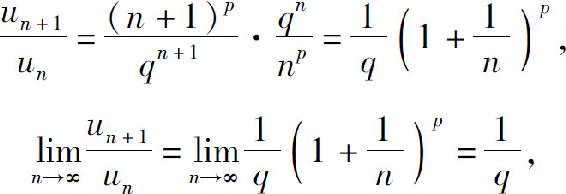
所以，当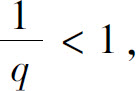
即q＞1时，级数收敛；当
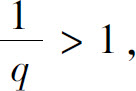即q＜1时，级数发散；而当q＝1时，级数为
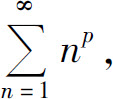显然发散．
例6 讨论级数
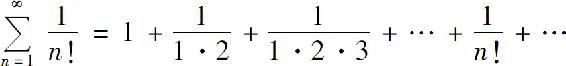
的收敛性．
解法1（利用比较判别法）当n≥2时，
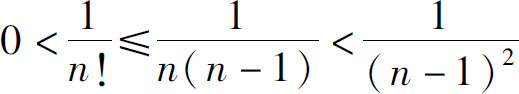
而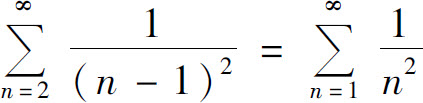
收敛，所以所给级数收敛．
解法2（利用比值判别法）因为
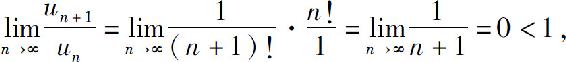
所以所给级数收敛．
下面不加证明地给出另一判别正项级数收敛性的强有力工具——根值判别法．
定理5（根值判别法）设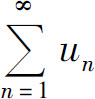
为正项级数，如果
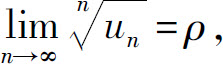
则 （1）当ρ＜1时，级数收敛；
（2）当ρ＞1（或ρ＝∞）时，级数发散；
（3）当ρ＝1时，级数可能收敛也可能发散．
例7 讨论级数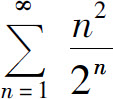
的收敛性．
解 因为
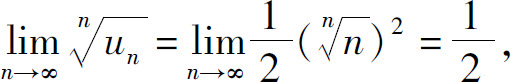
所以所给级数收敛（这里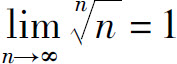
）．
习题8.2
1．用比较判别法及其极限形式判定下列级数的收敛性：
（1）
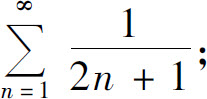
（2）
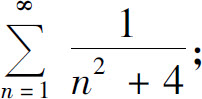
（3）
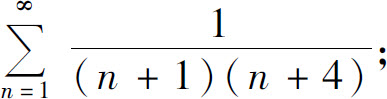
（4）
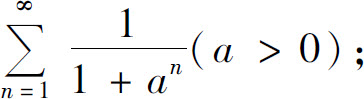
（5）
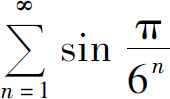
（6）
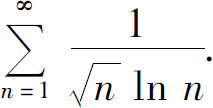
2．用比值判别法判定下列级数的收敛性：
（1）
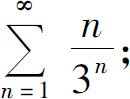
（2）
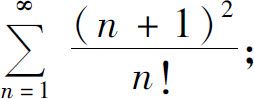
（3）
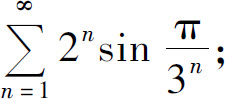
（4）
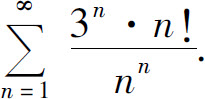
3．用根值判别法判定下列级数的收敛性：
（1）
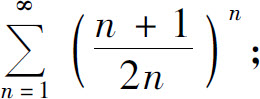
（2）
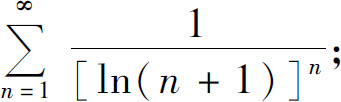
（3）
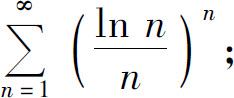
（4）
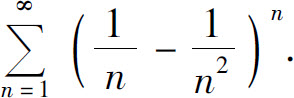
4．确定下列级数的收敛性：
（1）
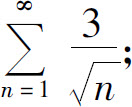
（2）
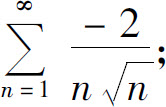
（3）
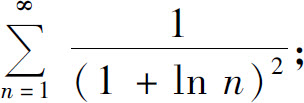
（4）
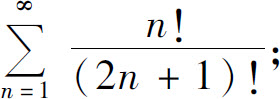
5．利用级数收敛的必要条件证明：