2.5 微分
2.5 微分
2.5.1 微分的概念
先考察一个具体问题.
设有一边长为x0的正方形金属薄片，受温度的影响其边长变为x0＋Δx，相应的正方形面积的增量为
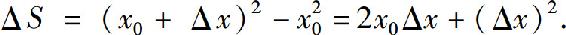
可见ΔS由两部分组成.第一部分为2x0Δx（即图2.3中阴影部分的面积）是Δx的线性函数，第二部分（Δx）2是当Δx→0时比Δx高阶的无穷小.由此可知，当给x0一个微小增量Δx时，由此引起的正方形面积增量ΔS可以近似地用第一部分来近似，产生的误差是一个比Δx高阶的无穷小．
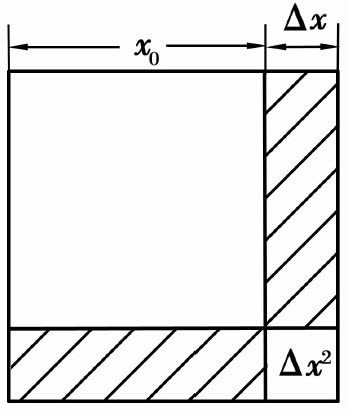
图2.3
定义1 设函数y＝f（x）在点x0的某邻域内有定义，x0＋Δx在此邻域内，如果函数增量Δy＝f（x0＋Δx）-f（x0）可表示为
其中A是与Δx无关的常数，则称函数f（x）在点x0可微，并称AΔx为f（x）在点x0的微分，记为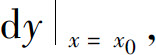
即
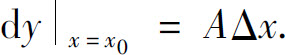
函数微分AΔx是Δx的线性函数，且与函数增量Δy相差一个比Δx高阶的无穷小．当A≠0时，它是Δy的主要部分，所以也说微分dy是增量Δy的线性主部．当|Δx|很小时，就可以用微分dy来近似增量Δy．
下面讨论函数可微的条件．
设f（x）在点x0可微，由式（1）有
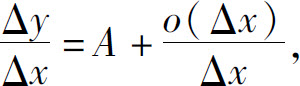
两边取极限得
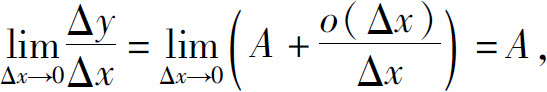
所以f（x）在点x0可导，并且
f′（x0）＝A．
反之，若f（x）在点x0可导，即
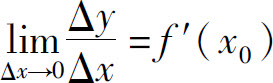
存在，根据极限与无穷小的关系，有
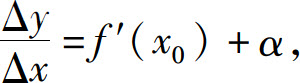
其中当Δx→0时α→0．因而
Δy＝f′（x0）·Δx＋α·Δx．
这表明函数增量Δy可表示为Δx的线性部分f′（x0）Δx与比Δx高阶的无穷小之和，所以f（x）在点x0可微，且有
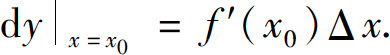
因此，有如下定理：
定理 函数f（x）在点x0可微的充要条件是函数f（x）在点x0可导，并有
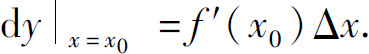
若函数y＝f（x）在区间I上每一点都可微，则称f（x）为I上的可微函数．函数y＝f（x）在I上任一点x处的微分记作
它不仅依赖于Δx，而且也依赖于x．
特别当f（x）＝x时，则f′（x）＝1．代入公式dy＝f′（x）Δx得dx＝Δx，即自变量x的微分dx就是它的增量Δx．于是函数y＝f（x）的微分又可记为
两边除以dx，得
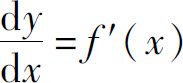
也就是说，函数微分dy与自变量微分dx的商就等于该函数的导数，故导数也称为微商．
例1 设y＝x2，求dy，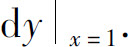
解 因为y′＝（x2）′＝2x，所以
dy＝2xdx．
又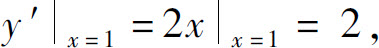
所以
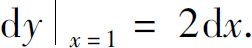
2.5.2 微分的几何意义
设函数f（x）在点x0处可微．如图2.4所示，过曲线y＝f（x）上点P0（x0，y0）作切线P0T，设P0T的倾角为α，则tanα＝f′（x0）．
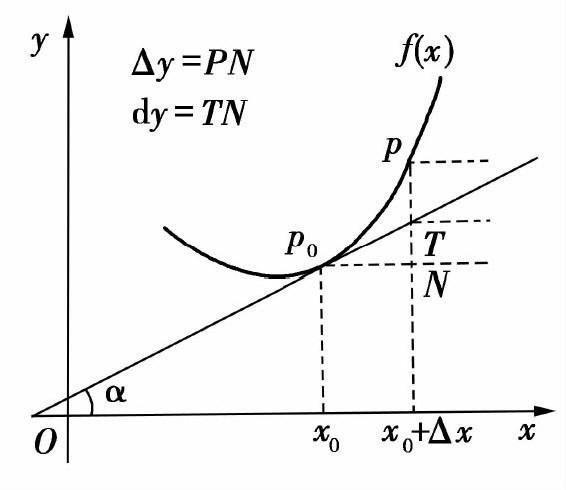
图2.4
当x从x0变化到x0＋Δx时，切线P0T上的点的纵坐标有相应的增量
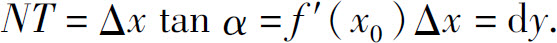
由此可见，函数f（x）在点x0处的微分dy就是曲线y＝f（x）在点P0（x0，y0）处切线上点的纵坐标的增量．
当|Δx|很小时，|Δy-dy|比|Δx|小得多．因此在点P0的邻近，可以用切线段来近似代替曲线段．
2.5.3 微分的运算法则
根据函数导数与微分的关系，可推出如下的微分运算法则：
（1）
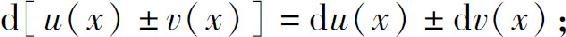
（2）
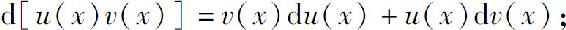
（3）
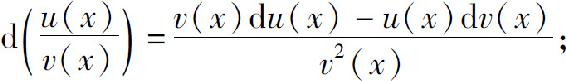
（4）
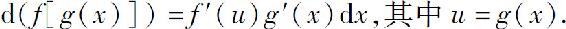
在上述复合函数的微分运算法则（4）中，由于du＝g′（x）dx，所以它也可写作
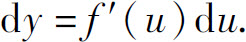
这与式（3）在形式上完全相同．因此，对于函数y＝f（u），无论u为自变量还是中间变量，它的微分形式都是dy＝f（u）du．这个性质通常称为一阶微分形式的不变性．
例2 求y＝x ln x＋x的微分．
解
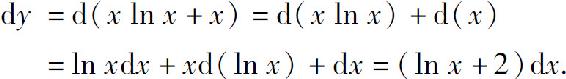
例3 求y＝esin（ax＋b）的微分．
解 由一阶微分形式不变性，可得
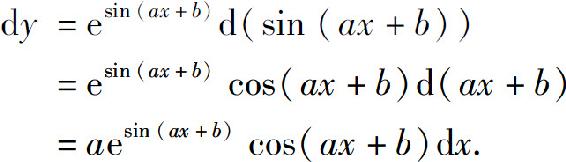
例4 在下列等式左端的括号中填上适当的函数，使等式成立．
（1）d（ ）＝2x2dx；
（2）d（ ）＝sin atdt（a≠0）．
解 （1）因为 d（x3）＝3x2dx，
所以
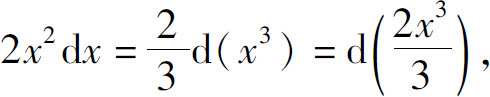
即
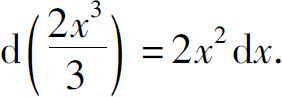
一般地
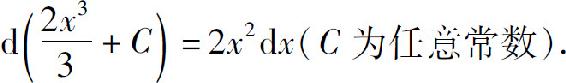
（2）因为
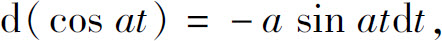
所以
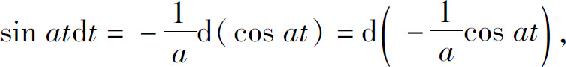
即
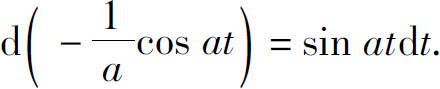
一般地
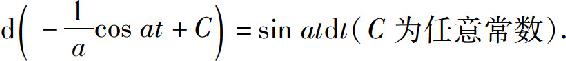
2.5.4 微分在近似计算中的应用
微分在数学中有许多重要的应用．这里只介绍它在近似计算方面的应用．
由函数增量与微分的关系
Δy＝f′（x0）Δx＋α·Δx＝dy＋α·Δx
其中Δx→0时α→0．当|Δx|较小时，有Δy≈dy，因此即得
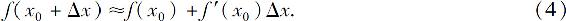
令x＝x0＋Δx，有
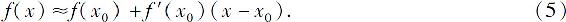
如果f（x0）与f′（x0）都容易计算，那么可利用式（4）来近似计算f（x0＋Δx）或利用式（5）来近似计算f（x）．
令x0＝0，则由式（5）可得一些函数在原点附近的近似公式：
（1）sin x≈x；
（2）tan x≈x；
（3）ln（1＋x）≈x；
（4）ex≈1＋x；
（5）
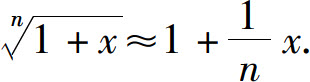
例5 求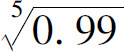
的近似值．
解 方法一 设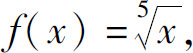
取x0＝1，Δx＝-0.01．由于
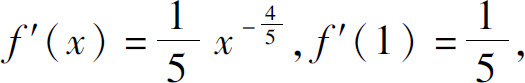
由式（4）可得
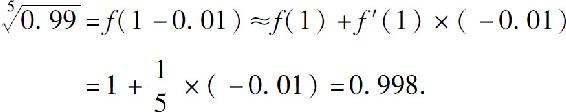
方法二 直接利用近似公式：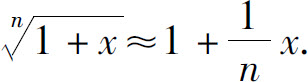
取x＝-0.01，故
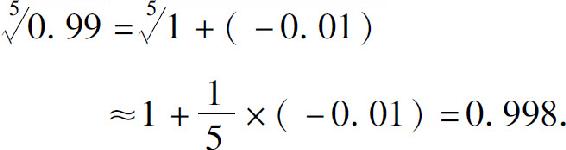
习题2.5
1．对指定的x及dx，求dy：
（1）y＝（x2＋5）3，x＝1，dx＝-0.01；
（2）
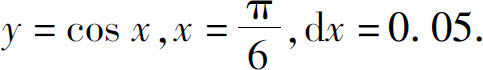
2．求下列函数的微分：
（1）
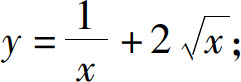
（2）y＝x ln x-x；
（3）y＝x2cos 2x；
（4）y＝e-xcos（3-x）；
（5）y＝tan2（1＋2x2）；
（6）
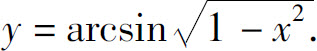
3．利用微分求近似值：
（1）
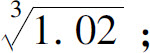
（2）ln（1.002）．