习题2

习题2

一、填空题

1．若f（x）在x＝x0处可导，则=_____．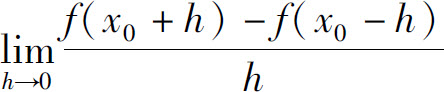

2．曲线y＝x ln x-x在点（e，0）处的切线方程为_____．

3．若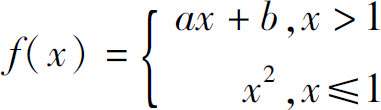在x＝1处可导，则a＝_____，b＝_____．

4．由方程2y-x＝sin y确定了y是x的隐函数，则dy＝_____．

5．设f（0）＝0且极限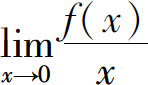存在，则_____．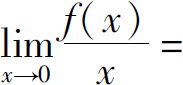

二、单项选择题

1．下列结论正确的是（　　）．

A．f（x）在点x0连续，则在点x0可导
B．f（x）在点x0可导，则在点x0连续
C．f（x）在点x0连续，则在点x0可微
D．f（x）当x→x0时极限存在，则在点x0连续

2．设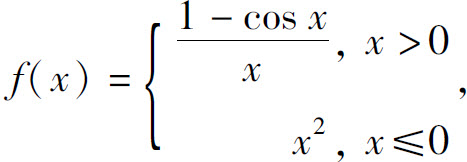则f（x）在x＝0处（　　）．

A．不连续
B．连续，但不可导
C．可导
D．不仅可导，且导数连续

3．设f′（x0）＝2，则当x→x0时，f（x）在x＝x0处的微分dy是（　　）．

A．比Δx低阶无穷小
B．比Δx高阶无穷小
C．与Δx同阶但非等价的无穷小
D．与Δx等价无穷小

4．设f（x）＝x（x-1）（x-2）…（x-99），则f′（0）＝（　　）．

A．99
B．-99
C．99！
D．-99！

5．设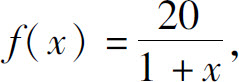且f（x0）＝5，则f［f′（x0）］＝（　　）．

A．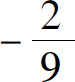
B．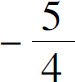
C．80
D．-80

三、解答题

1．求下列函数的导数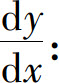

（1）

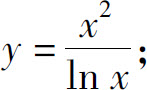
（2）

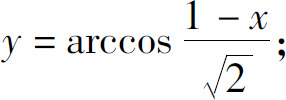
（3）

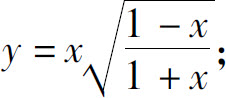
（4）

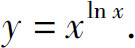
2．求由参数方程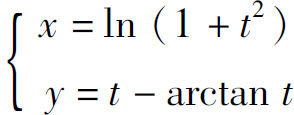所确定的函数的二阶导数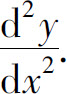

3．求函数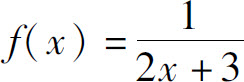在x＝0处的n阶导数f（n）（0）．