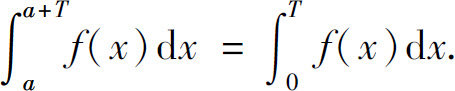5.3　定积分的换元积分法与分部积分法

5.3　定积分的换元积分法与分部积分法

第4章讨论了用换元积分法和分部积分法求已知函数原函数的问题，为了简化定积分的计算过程，下面引入定积分的换元积分法与分部积分法．

5.3.1　换元积分法

定理　设函数f（x）在区间［a，b］上连续，作变换x＝φ（t），如果

（1）φ（α）＝a，φ（β）＝b；

（2）φ（t）在区间［α，β］（或［β，α］）上单调且有连续导数，则有

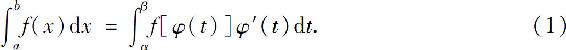
证　因为f（x）在［a，b］上连续，所以f（x）在区间［a，b］上可积，设F（x）是f（x）的一个原函数，由牛顿—莱布尼兹公式

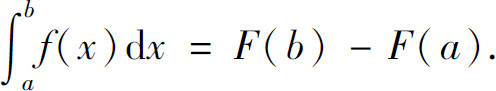
另一方面，由于

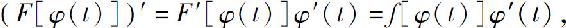
所以函数F［φ（t）］是函数f［φ（t）］φ′（t）的一个原函数．因此有

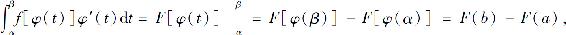
于是有

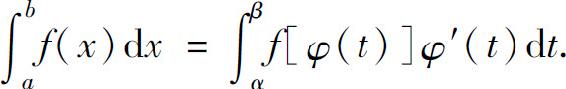
公式（1）称为定积分的换元公式．应用它求定积分时，在作变量代换的同时，相应的积分限也作了改变，这样就省去了变量的回代过程，计算也就比较简单．另外还应注意到式（1）的应用是双向的，即

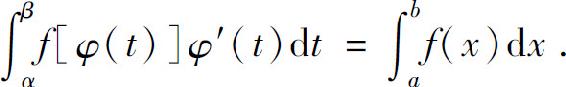
例1　求定积分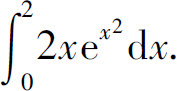

解　取u＝x2，则du＝2xdx，当x＝0时，u＝0；当x＝2时，u＝4，于是

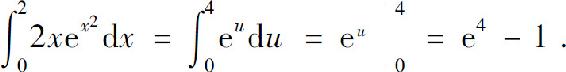
也可用下面的解法：

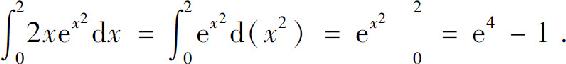
这一解法没有引入新的积分变量，计算时原积分的上下限不要改变．这实际上是用“凑微分”求函数的积分，相对于前面的解法要简明一些．

例2　计算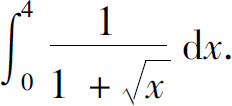

解　设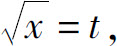则dx＝2tdt，且当x＝0时，t＝0；当x＝4时，t＝2．所以

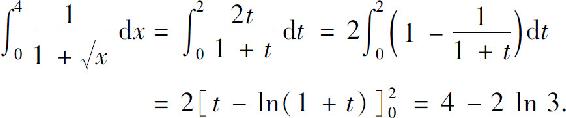
例3　计算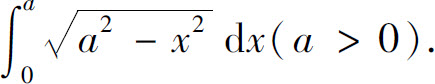

解　设x＝a sin t，则dx＝a cos tdt，且当x＝0时，t＝0；当x＝a时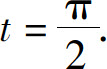，所以

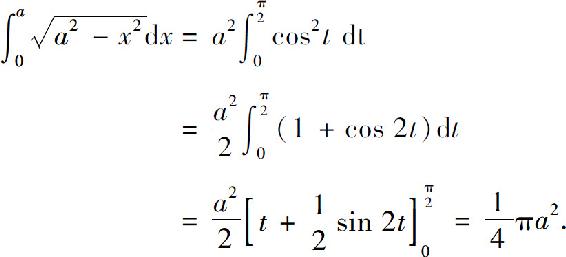
例4　设函数f（x）在区间［－a，a］上连续，则

（1）当f（x）为奇函数时，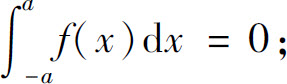

（2）当f（x）为偶函数时，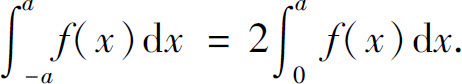

证　（1）由定积分的可加性，有

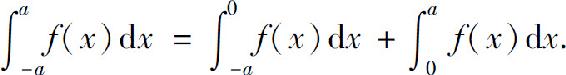
对于定积分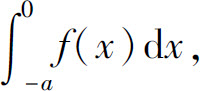令x＝－t，则dx＝－dt，且当x＝－a时，t＝a；当x＝0时，t＝0．于是

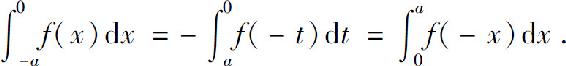
当f（x）为奇函数时，f（－x）＝－f（x），故

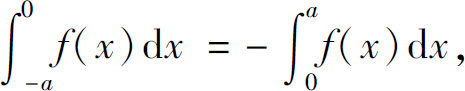
所以

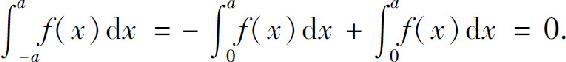
类似可证明（2）．

利用本例的结论，往往可简化对称区间上定积分的计算．

例5　求定积分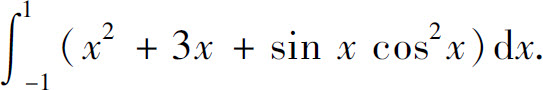

解　因为3x与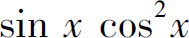都是对称区间［－1，1］上的奇函数，所以

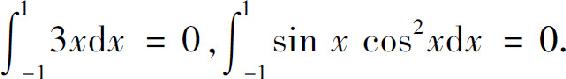
因此

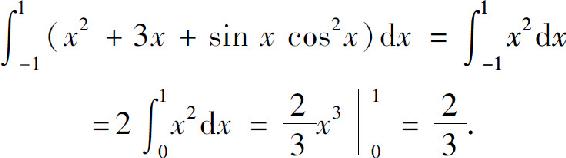
5.3.2　分部积分法

设函数u（x）与v（x）在区间［a，b］上有连续的导数u′（x），v′（x），则有

（uv）′＝u′v＋uv′．

两边从a到b求定积分，有

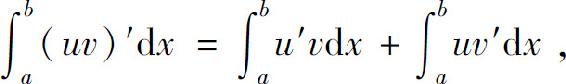
即

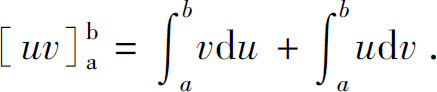
移项得

式（2）称为定积分的分部积分公式．

例6　计算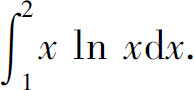

解

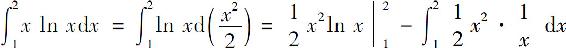
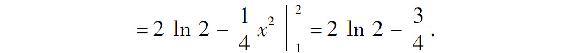
例7　计算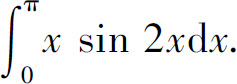

解

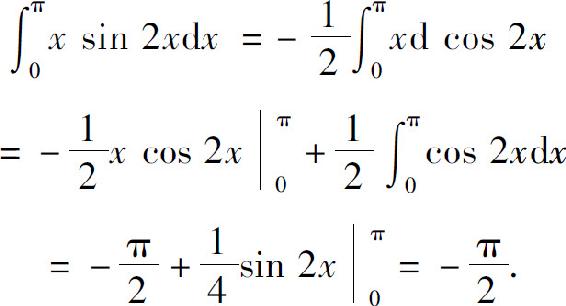
例8　计算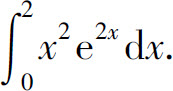

解

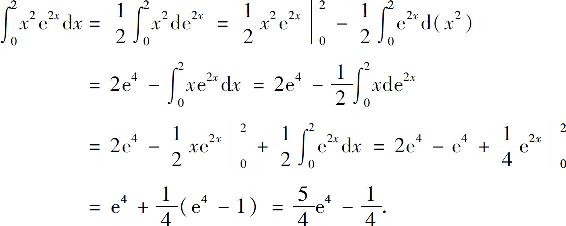
例9　计算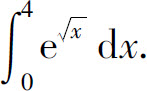

解　先用定积分的换元法，再用定积分的分部积分法．

设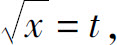则dx＝2tdt，且当x＝0时，t＝0；当x＝4时，t＝2，所以

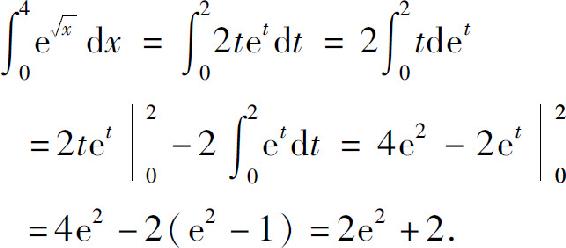
例10　计算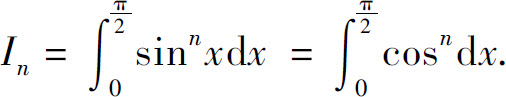（n为自然数）

解　先证明等式成立．

令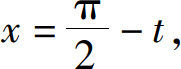则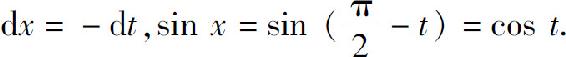又当x＝0时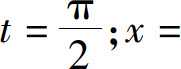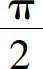，时，t＝0．于是

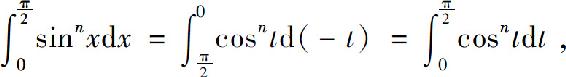
即

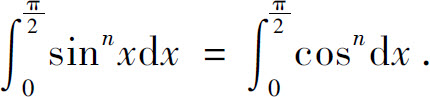
下面计算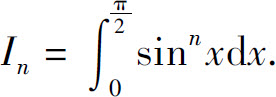由定积分的分部积分公式得

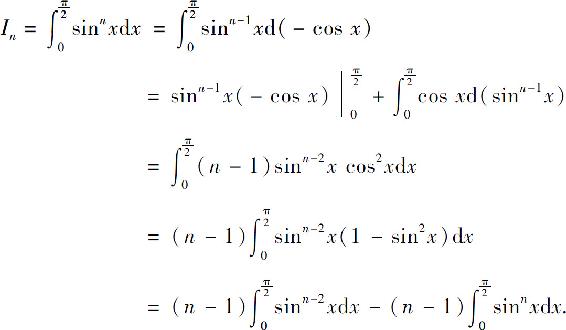
移项整理，得

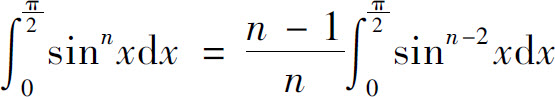
即为递推公式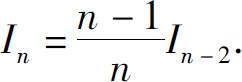又

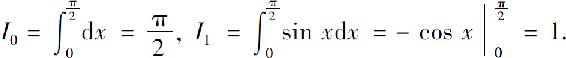
根据递推公式可以推出

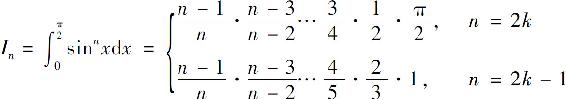
例如

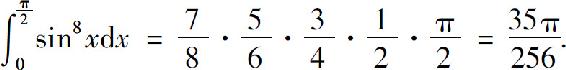
习题5.3

1．计算下列定积分：

（1）

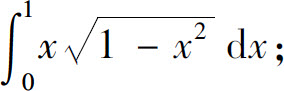
（2）

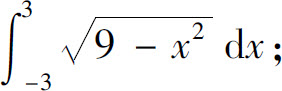
（3）

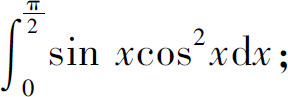
（4）

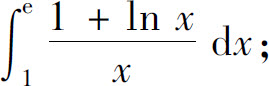
（5）

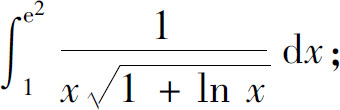
（6）

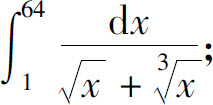
（7）

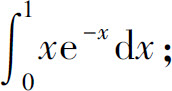
（8）

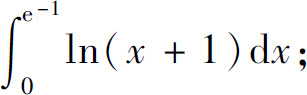
（9）

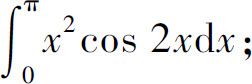
（10）

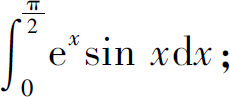
（11）

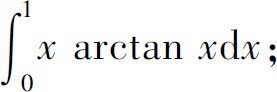
（12）

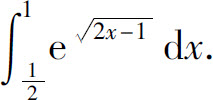
2．已知f″（x）在［0，2］上连续，且f（0）＝1，f（2）＝3，f′（2）＝5，试求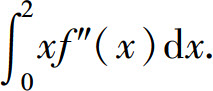

3．设f（x）是连续函数，证明：

（1）当f（x）是偶函数时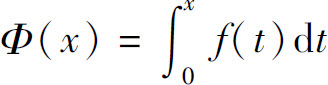，是奇函数；

（2）当f（x）是奇函数时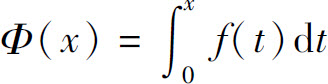，是偶函数．

4．设f（x）是一个以T为周期的连续周期函数．试证明对于任意常数a，有