1.3 函数极限
1.3 函数极限
1.3.1 x趋于∞时函数的极限
因为数列{an}可以理解为定义域为正整数集Z+的函数:an=f(n),所以数列{an}的极限为A是指:对于ᗄε>0,Ǝ正整数N,当n>N时,就有∣f(n)-A∣<ε.把数列极限定义中的函数为f(n)而自变量n只取正整数值的特殊性撇开,可以引出x→+∞时函数极限的定义.
定义1 设函数f(x)在区间[a,+∞)上有定义,A是常数.若对任意给定的正数ε,总存在某个正数X,使得当x>X时都有
∣f(x)-A∣<ε,
则称A为函数f(x)当x→+∞时的极限,记为
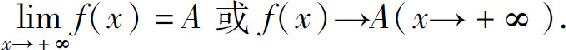
类似地,我们可以给出x→∞,x→-∞时函数极限的定义.
定义2 设函数f(x)当∣x∣≥a时有定义,A是常数.若对任意给定的正数ε,总存在某个正数X,使得当|x|>X时有
∣f(x)-A∣<ε,
则称A为函数f(x)当x→∞时的极限,记为
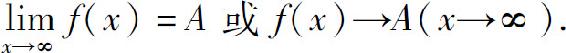
从几何上看, 表示:对于任意给定的正数ε,总能找到某个正数X,使得函数f(x)在区间(-∞,-X)和(X,+∞)内的图形位于直线y=A-ε与y=A+ε之间,如图1.10所示.
表示:对于任意给定的正数ε,总能找到某个正数X,使得函数f(x)在区间(-∞,-X)和(X,+∞)内的图形位于直线y=A-ε与y=A+ε之间,如图1.10所示.
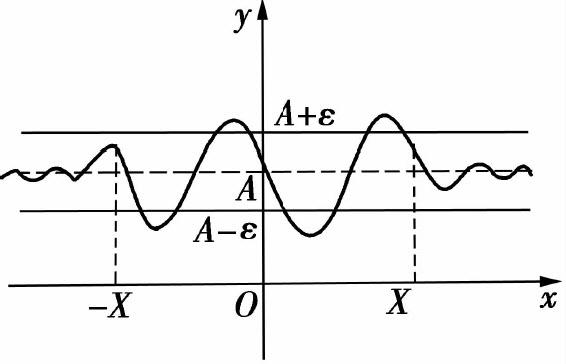
图1.10
例1 证明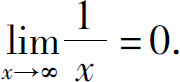
证 对于ᗄε>0,取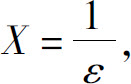 则当∣x∣>X时,有
则当∣x∣>X时,有
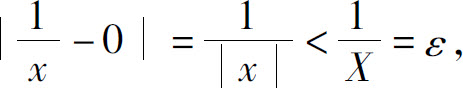
所以
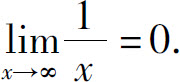
1.3.2 x趋于x0时函数的极限
1)概念
现在讨论当自变量x无限接近某一有限值x0时,函数f(x)的变化趋势.
考察当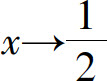 时,函数
时,函数
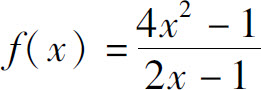
的变化趋势.
当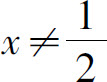 时,f(x)=2x-1,由图1.11可见,当x无限地接近
时,f(x)=2x-1,由图1.11可见,当x无限地接近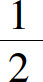 (但不等于
(但不等于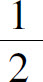 )时,对应函数值无限地接近常数2.我们称数2为函数
)时,对应函数值无限地接近常数2.我们称数2为函数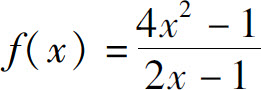 当
当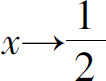 时的极限.
时的极限.
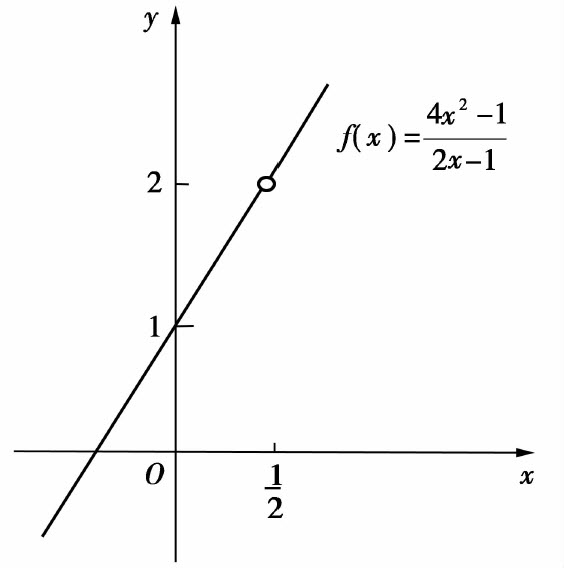
图1.11
一般地,设函数f(x)在x0的某去心邻域内有定义,如果当自变量x无限接近x0时,对应的函数值f(x)无限接近于常数A,则称A为函数f(x)当x→x0时的极限.
在x→x0的过程中,对应的函数值f(x)无限接近于常数A,即∣f(x)-A∣<ε,其中ε是可以任意小的正数.而x→x0(x≠x0)可用0<∣x-x0∣<δ来刻画,其中δ是某个正数.因此有下述定义:
定义3 设函数f(x)在x0的某个去心邻域内有定义,A是常数.若对任给的正数ε,总存在某个正数δ,使得当0<∣x-x0∣<δ时都有
∣f(x)-A∣<ε,
则称A为函数f(x)当x→x0时的极限,记为
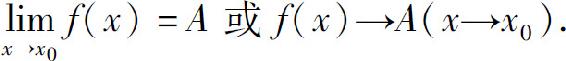
这个定义称为函数极限的ε-δ定义.
定义中0<∣x-x0∣表示x≠x0,所以f(x)当x→x0的极限是否存在与函数在该定点x0处有无定义没有关系.
2)几何意义
因为0<∣x-x0∣<δ,即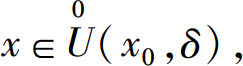 所以
所以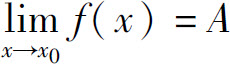 表示:对任意给定的正数ε,总存在一个正数δ,使得函数f(x)在
表示:对任意给定的正数ε,总存在一个正数δ,使得函数f(x)在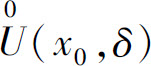 内的图形位于两条直线y=A-ε与y=A+ε之间,如图1.12所示.
内的图形位于两条直线y=A-ε与y=A+ε之间,如图1.12所示.
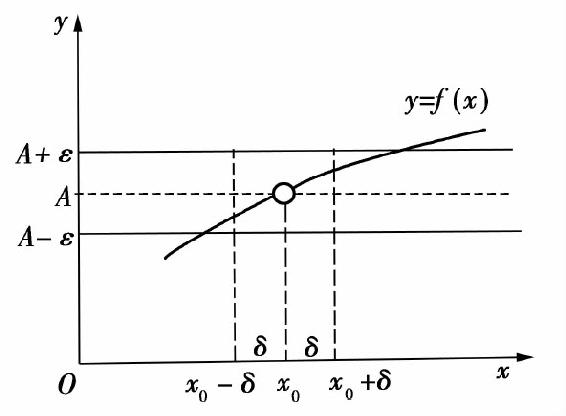
图1.12
由于正数ε可以任意小(一般δ相应变小),从而直线y=A-ε与y=A+ε所围的窄条可任意窄,这就表明函数值可以无限接近于A.
例2 证明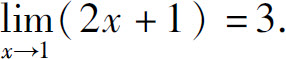
证 由于
∣f(x)-A∣=∣(2x+1)-3∣=∣2(x-1)∣=2∣x-1∣,
对于ᗄε>0,要使∣f(x)-A∣<ε,只要2∣x-1∣<ε.
取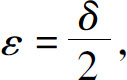 则当0<∣x-1∣<δ时,就有
则当0<∣x-1∣<δ时,就有
∣(2x+1)-3∣<ε,
故
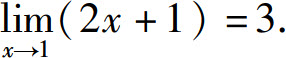
例3 证明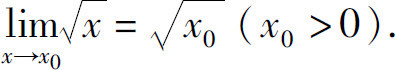
证
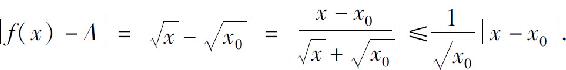
对ᗄε>0,要使∣f(x)-A∣<ε,只要∣x-x0∣<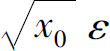 且x≥0,而x≥0可用∣x-x0∣<x0保证.
且x≥0,而x≥0可用∣x-x0∣<x0保证.
取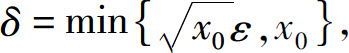 则当0∣<x-x0∣<δ时,就有
则当0∣<x-x0∣<δ时,就有
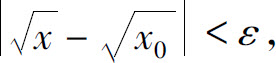
所以
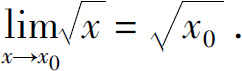
3)单侧极限
函数极限定义中“x→x0”是指x从x0的左右两侧趋向x0.有些函数在其定义域上某些点左侧与右侧的解析式不同,或仅在某些点的一侧有定义,这时需要考虑x从x0的一侧趋向x0时函数的变化趋势.
定义4 设函数f(x)在(x0,x0+h)(或(x0-h,x0))(h>0)内有定义,A是常数.若对于任意给定的正数ε,总存在某个正数δ,使得当x0<x<x0+δ(或x0-δ<x<x0)时都有
∣f(x)-A∣<ε,
则称A为函数f(x)当x→x0时的右极限(或左极限),记为
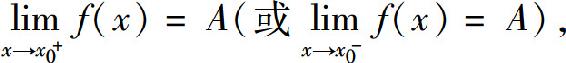
或者
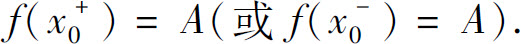
右极限与左极限统称为单侧极限.
由定义容易证明: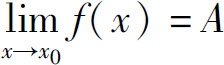 的充要条件是
的充要条件是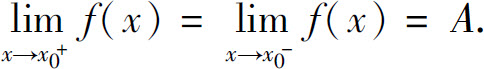
由上述结论可知,如果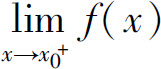 和
和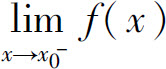 至少有一个不存在或两个都存在但不相等,则
至少有一个不存在或两个都存在但不相等,则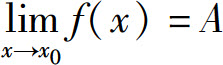 一定不存在.由于分段函数在分段点两侧的表达式不同,因此分段函数在分段点处的极限可通过左右极限来讨论.
一定不存在.由于分段函数在分段点两侧的表达式不同,因此分段函数在分段点处的极限可通过左右极限来讨论.
例4 讨论符号函数
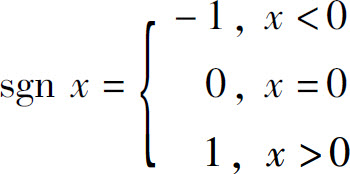
当x→0时的极限.
解
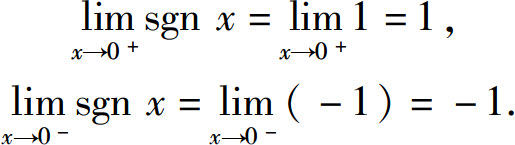
故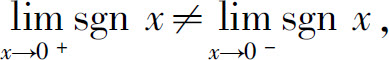 所以当x→0时sgnx的极限不存在.
所以当x→0时sgnx的极限不存在.
1.3.3 函数极限的性质
前面给出了下述6种类型的函数极限:
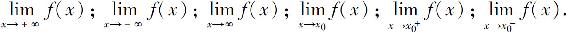
它们具有与数列极限相类似的一些性质,下面仅以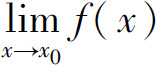 为例来叙述这些性质,至于其他类型的极限,只要作出相应修改即可.
为例来叙述这些性质,至于其他类型的极限,只要作出相应修改即可.
性质1 (唯一性) 如果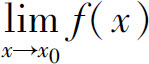 存在,那么这极限唯一.
存在,那么这极限唯一.
性质2 (局部有界性) 如果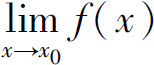 存在,则f(x)在x0的某个去心邻域内有界.
存在,则f(x)在x0的某个去心邻域内有界.
证 设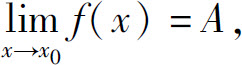 取ε=1,则存在δ>0,使得对一切
取ε=1,则存在δ>0,使得对一切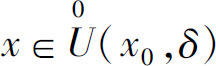 有
有
∣f(x)-A∣<1,
故
∣f(x)∣≤∣f(x)-A∣+∣A∣≤1+∣A∣.
所以f(x)在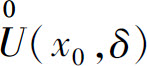 内有界.
内有界.
性质3(局部保号性) 若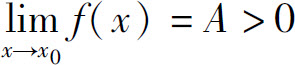 (或A<0),则在x0的某个去心邻域内f(x)>0(或f(x)<0).
(或A<0),则在x0的某个去心邻域内f(x)>0(或f(x)<0).
证 设A>0.由于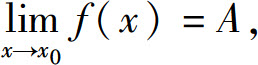 对
对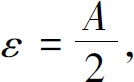 则存在δ>0,当0<∣x-x0∣<δ时,
则存在δ>0,当0<∣x-x0∣<δ时,
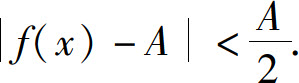
故
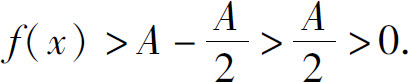
从上面的证明可得如下结论:
推论1 若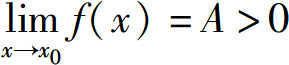 (或A<0),则在x0的某个去心邻域内
(或A<0),则在x0的某个去心邻域内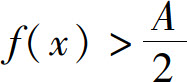 (或f(x)<
(或f(x)<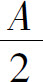 ).
).
推论2 若在x0的某个去心邻域内f(x)≥0(或f(x)≤0),且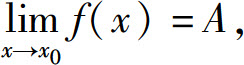 则A≥0(或A≤0).
则A≥0(或A≤0).
1.3.4 函数极限的运算
定理1(四则运算法则) 若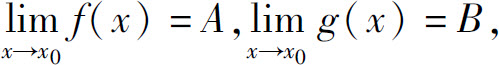 则
则
(1)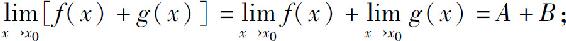
(2)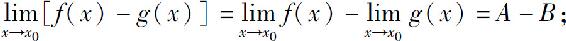
(3)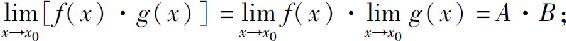
(4)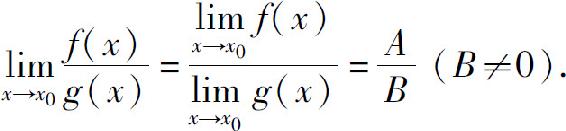
证 只证(3).
由于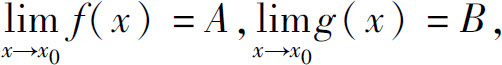 所以对任意给定的ε>0,分别存在δ1>0与δ2>0,使得当0<∣x-x0∣<δ1时有
所以对任意给定的ε>0,分别存在δ1>0与δ2>0,使得当0<∣x-x0∣<δ1时有

当0<∣x-x0∣<δ2时有

又
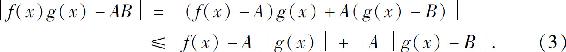
由局部有界性,存在M>0,δ3>0,使得当0<∣x-x0∣<δ3时,有
∣g(x)∣<M.
令δ=min{δ1,δ2,δ3},则当0<∣x-x0∣<δ时,式(1),(2),(3)同时成立,故有
∣f(x)g(x)-AB∣<(M+∣A∣)ε.
由ε的任意性,证得
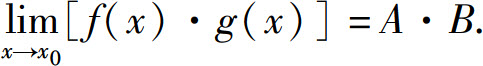
定理中的(1)和(3)可推广到有限个函数的情形,并由(3)可得以下推论.
推论1 若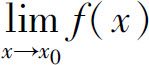 存在,C为常数,则
存在,C为常数,则
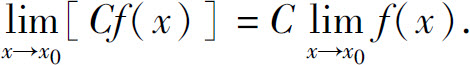
即在求极限时,常数可提到极限符号外.
推论2 若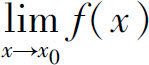 存在,n为正整数,则
存在,n为正整数,则
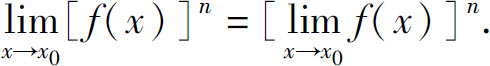
例5 求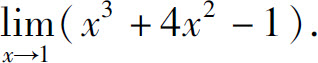
解
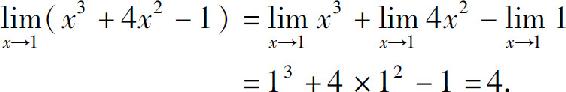
例6 求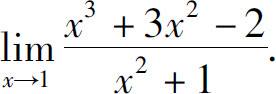
解
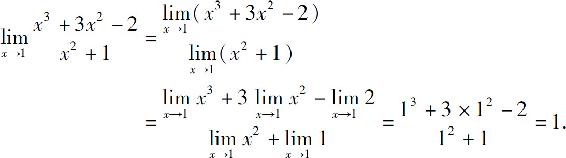
一般地,可用代入法求有理函数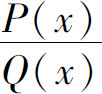 的极限,其中P(x)和Q(x)是多项式:
的极限,其中P(x)和Q(x)是多项式:
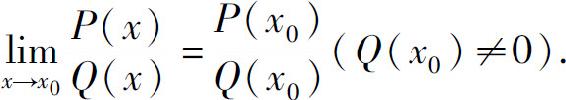
例7 求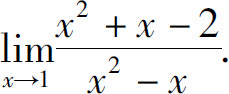
解 不能代入x=1,因为此时分母为零.但当x≠1时
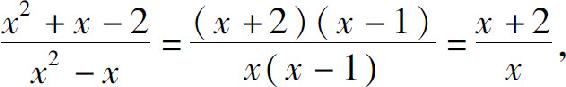
所以
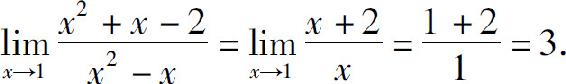
例8 求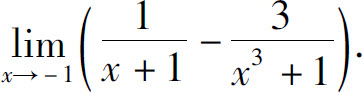
解
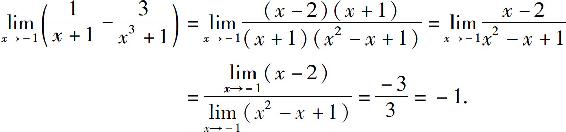
例9 求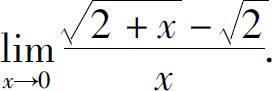
解
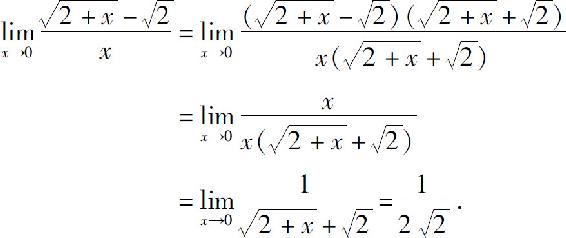
定理2(复合函数的极限) 设函数y=f[φ(x)]是函数u=φ(x),y=f(u)的复合函数.如果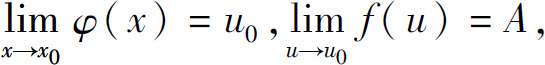 且在x0的某个去心邻域内φ(x)≠u0,则
且在x0的某个去心邻域内φ(x)≠u0,则
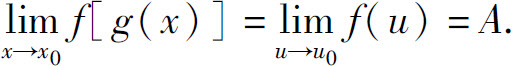
定理对x→∞时的情形也成立.定理说明,在满足定理的条件下,可通过变量代换u=φ(x)把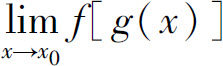 化为
化为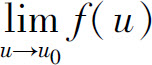 来计算.
来计算.
习题1.3
1.根据极限定义证明:
(1)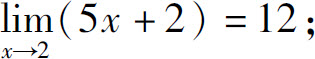
(2)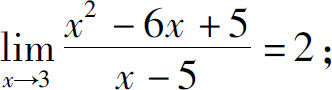
(3)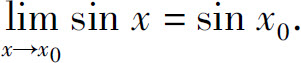
2.求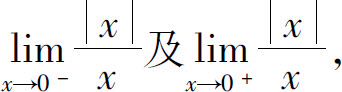 并说明
并说明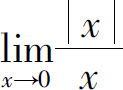 是否存在.
是否存在.
3.求下列极限:
(1)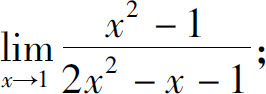
(2)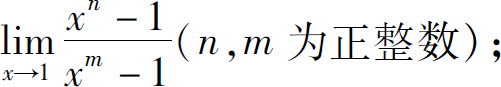
(3)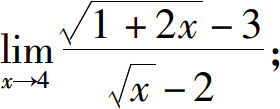
(4)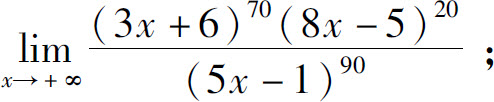
(5)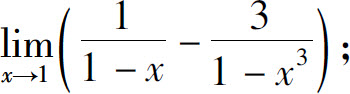
(6)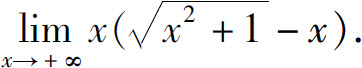
4.证明:如果 则
则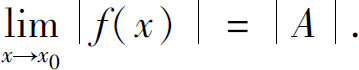 试举例说明逆命题不成立.
试举例说明逆命题不成立.
