2.2 求导法则
2.2 求导法则
本节将引入几个基本的求导法则，利用这些法则和基本初等函数的导数公式，就能较简便地求出常见的初等函数的导数．
2.2.1 函数四则运算的求导法则
定理1 如果函数u（x）和v（x）在点x可导，则它们的和、差、积、商（分母为零的点除外）在点x可导，并且
（1）
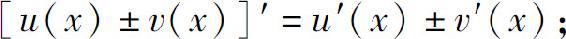
（2）
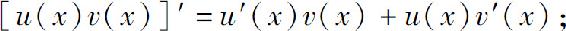
（3）
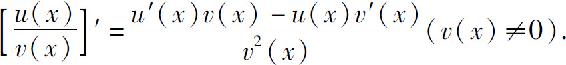
以上三个法则都可用导数定义和极限运算法则来证明，我们只给出法则（2）的证明．
证 因为
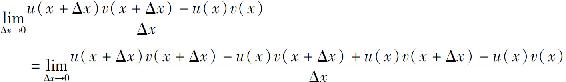
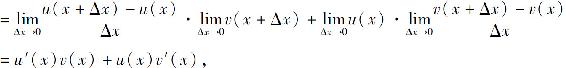
所以u（x）v（x）在点x可导，并且
［u（x）v（x）］′＝u′（x）v（x）＋u（x）v′（x）．
法则（2）可简单地表示为
（uv）′＝u′v＋uv′．
定理中的（1），（2）可推广到任意有限个可导函数的情形．例如
（uvw）′＝u′vw＋uv′w＋uvw′．
由定理中的（2），（3）可得到两种特殊的情形：
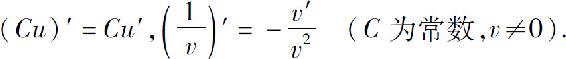
例1 设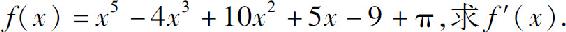
解
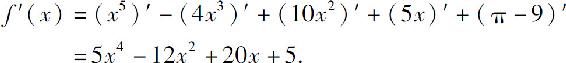
例2 设y＝sin x·ln x，求y′（π）．
解
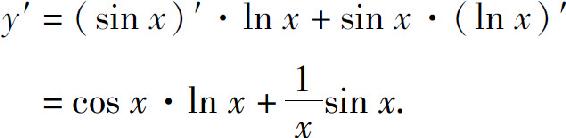
所以
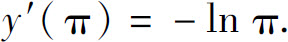
例3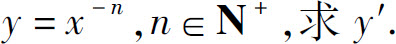 
解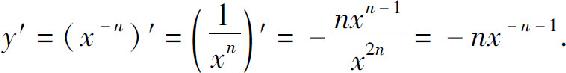 
例4 设y＝cot x，求y′．
解
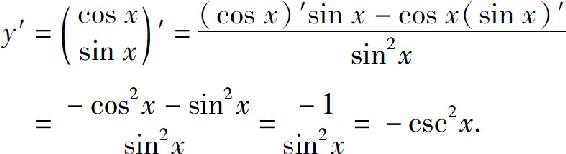
同理可得
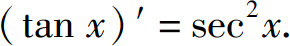
例5 设y＝sec x，求y′．
解
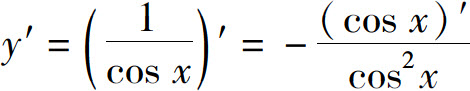
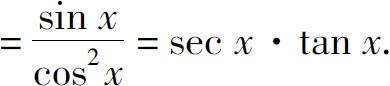
同理可得
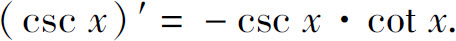
2.2.2 反函数的求导法则
定理2 如果函数x＝φ（y）在某区间内单调、可导且φ′（y）≠0，则它的反函数y＝f（x）在对应区间内可导，并且
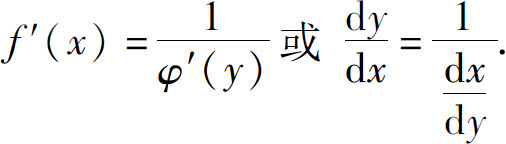
简单地说，即反函数的导数等于直接函数导数的倒数．
例6 求y＝ax的导数．
解 由于y＝ax，x∈（－∞，＋∞）为x＝logay，y∈（0，＋∞）的反函数，所以由定理2得
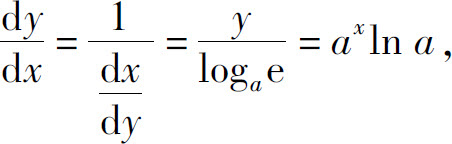
即
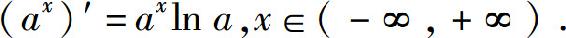
特别地，当a＝e时
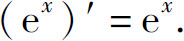
例7 求y＝arcsin x，x∈（－1，1）的导数．
解 由于y＝arcsin x，x∈（－1，1）是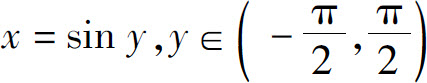
的反函数，所以
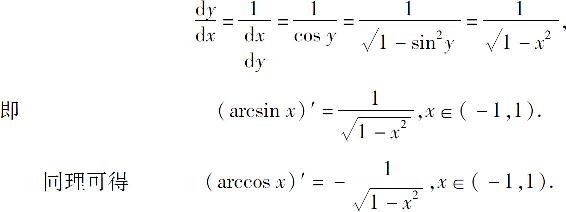
例8 求y＝arctan x的导数．
解 由于y＝arctan x，x∈（－∞，＋∞）是x＝tan y，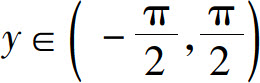
的反函数，所以
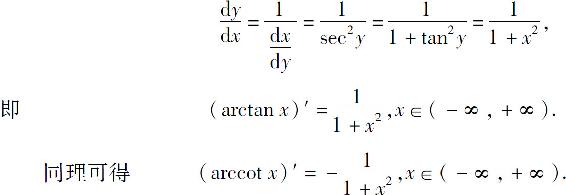
2.2.3 复合函数的求导法则
定理3 如果u＝φ（x）在点x处可导，y＝f（u）在对应点u＝φ（x）可导，则复合函数y＝f［φ（x）］在点x可导，且
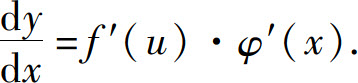
证 设x有增量Δx，相应u有增量Δu，从而y有增量Δy．由于f（u）在点u可导，因此
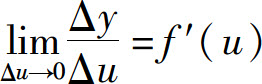
存在，根据极限与无穷小的关系有
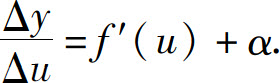
其中α是Δu→0时的无穷小．上式中Δu≠0，用Δu乘上式两边，得
Δy＝f′（u）·Δu＋α·Δu．
当Δu＝0时，由于Δy＝0，上式仍成立（这时取α＝0），于是
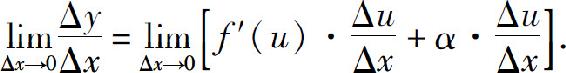
由于u＝φ（x）在点x可导，故在该点连续，于是当Δx→0时，Δu→0，从而
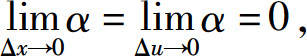
并且
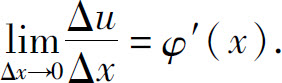
所以
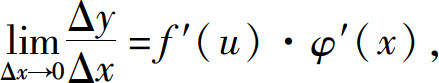
即
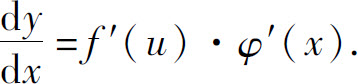
复合函数的求导公式亦称为链式法则．函数y＝f（u），u＝φ（x）的复合函数在点x的求导公式一般也写作
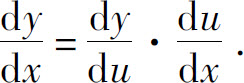
链式法则可以推广到多个中间变量的情形．例如，如果y＝f（u），u＝φ（v），v＝ψ（x）都可导，则复合函数y＝f（φ（ψ（x）））可导，并且
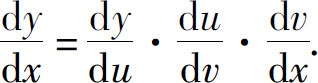
例9 求y＝cos x2的导数．
解 将y＝cos x2看作y＝cos u与u＝x2的复合函数，故
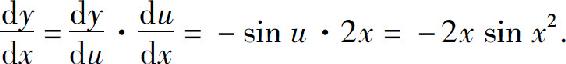
例10 求y＝ln｜x｜的导数．
解 当x＞0时，y＝ln x
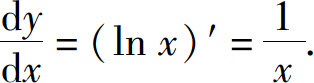
当x＜0时，y＝ln（－x）可看作y＝ln u与u＝－x的复合函数，故
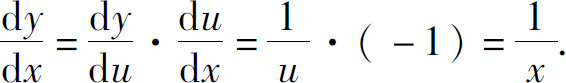
因此
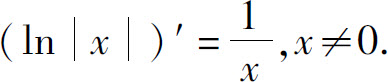
链式法则熟练后，中间变量可以不写出来，只要记住复合过程，弄清楚每一步“是在对谁求导”．
例11 设α为实数，求幂函数y＝xα（x＞0）的导数．
解
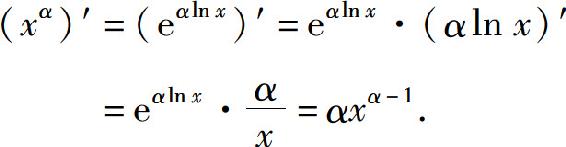
例12 求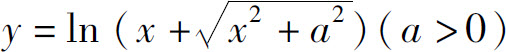
的导数．
解
2.2.4 基本求导法则与导数公式
现在把前面得到的求导法则与基本初等函数的导数公式列出如下：
1）函数四则运算的求导法则
设u（x）和v（x）在点x可导，则
（1）
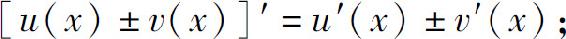
（2）
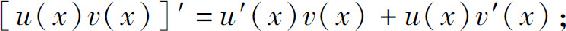
（3）
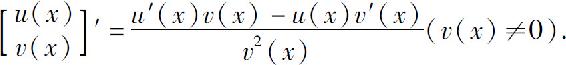
2）反函数的求导法则
设y＝f（x）是x＝φ（y）的反函数，φ′（y）≠0，则
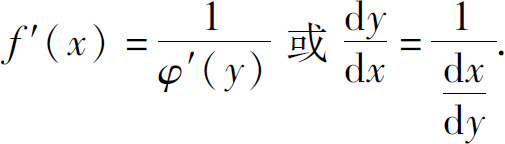
3）链式法则
设u＝φ（x）在点x处可导，y＝f（u）在相应点u＝φ（x）可导，则
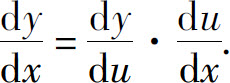
4）基本初等函数导数公式
（1）（C）′＝0．
（2）（xα）′＝αxα－1（α为任意实数）．
（3）（sin x）′＝cos x，（cos x）′＝－sin x．
（4）
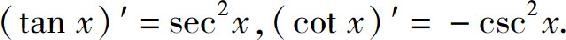
（5）（sec x）′＝sec x tan x，（csc x）′＝－csc x cot x．
（6）
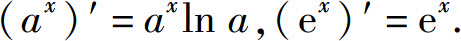
（7）
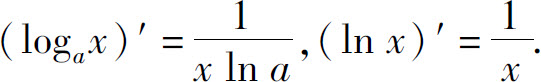
（8）
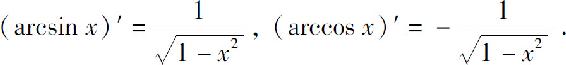
（9）
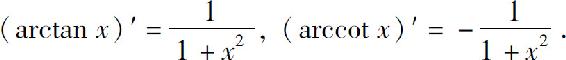
习题2.2
1．求下列函数的导数：
（1）
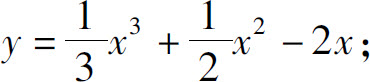
（2）
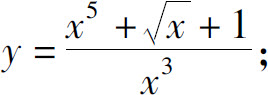
（3）
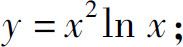
（4）
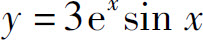
（5）
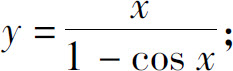
（6）
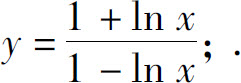
（7）
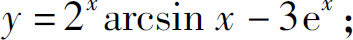
（8）
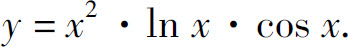
2．求下列复合函数的导数：
（1）y＝（1＋x2）5；
（2）
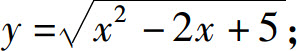
（3）y＝ln ln x；
（4）y＝arctan（2x＋1）；
（5）y＝ln（2－x＋3－x＋4－x）；
（6）
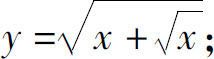
（7）
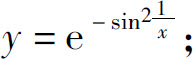
（8）y＝x arcsin（ln x）；
3．定义双曲函数如下：
双曲正弦函数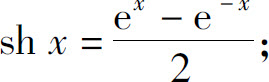
双曲余弦函数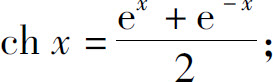
双曲正切函数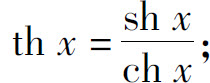
双曲余切函数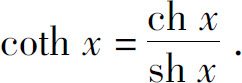
证明：
（1）（sh x）′＝ch x；
（2）（ch x）′＝sh x；
（3）
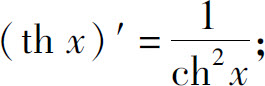
（4）
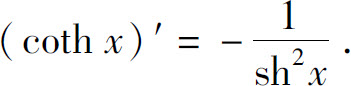
4．设f（x）可导，求下列函数的导数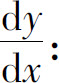
：
（1）y＝f（x2）；
（2）y＝f（tan x）＋tan（f（x））．