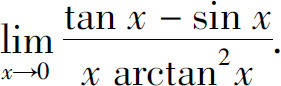1.5　无穷小与无穷大

1.5　无穷小与无穷大

1.5.1　无穷小

定义1　如果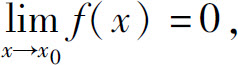则称f（x）为当x→x0时的无穷小．

例如，因为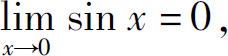所以函数sin x是当x→0时的无穷小．

类似可定义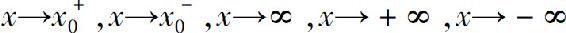时的无穷小．

特别地，以零为极限的数列｛an｝称为n→∞时的无穷小．

需要注意的是，无穷小是一个极限为零的函数（或数列），不是一个很小的数，因而与自变量的变化趋势密切相关．如函数是当x→∞时的无穷小，而当x趋于任何固定值时都不是无穷小．

由无穷小的定义及函数极限的四则运算法则，易知无穷小有如下性质：

性质1　有限个无穷小的代数和仍是无穷小．

性质2　有界函数与无穷小的乘积仍是无穷小．

例如，由于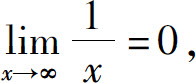且｜sin x｜≤1，所以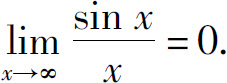

推论1　常数与无穷小的乘积仍是无穷小．

推论2　有限个无穷小的乘积仍是无穷小．

函数极限与无穷小有如下关系：

定理1　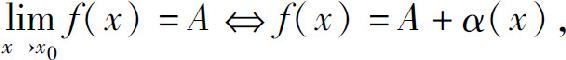其中α（x）是当x→x0时的无穷小．

证　充分性．因为α（x）是当x→x0时的无穷小，所以

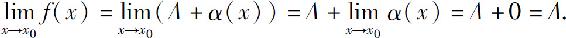
必要性．因为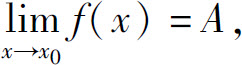所以

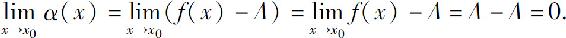
1.5.2　无穷大

如果在自变量的某一变化过程中，对应的函数值的绝对值｜f（x）｜无限增大，就称函数f（x）为这一变化过程中的无穷大．

定义2　设函数f（x）在x0的某个去心邻域内有定义．若对于任意给定的正数M，总存在正数δ，使得当0＜｜x－x0｜＜δ时，都有

｜f（x）｜＞M，

则称函数f（x）是当x→x0时的无穷大（或当x趋于x0时f（x）趋于无穷），记为

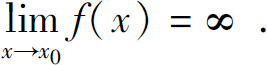
如果在定义中把｜f（x）｜＞M换成f（x）＞M（或f（x）＜－M），则称函数f（x）是当x→x0时的正无穷大（或负无穷大），记为

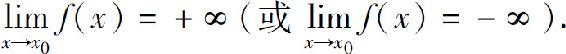
类似地，可以给出函数f（x）是当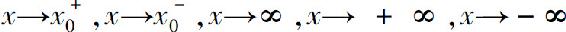时的无穷大的定义．例如：

定义3　设函数f（x）在［a，＋∞）上有定义．若对于任意给定的正数M，总存在正数X，使得当x＞X时，都有

｜f（x）｜＞M，

则称函数f（x）是当x→＋∞时的无穷大，记为

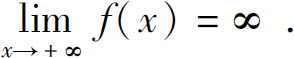
例如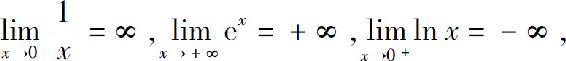，即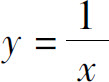是当x→0时的无穷大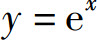，是当x→＋∞时的（正）无穷大，y＝ln x是当x→0＋时的（负）无穷大．

必须注意的是，无穷大不是一个数，不可与很大的数混为一谈．

由无穷大量与无穷小的定义，可推得它们之间有如下关系：

定理2　在自变量的同一变化过程中，如果f（x）为无穷大，则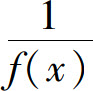为无穷小；反之，如果f（x）为无穷小，且f（x）≠0，则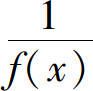为无穷大．

根据这个定理，对无穷大的研究可归结为对无穷小的讨论．

1.5.3　无穷小的比较

当x→0时，2x，x2与sin x都是无穷小．现在来考察它们的商当x→0时的极限：

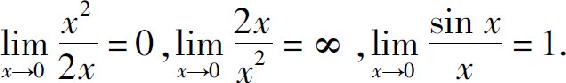
两个无穷小之比的极限的各种不同情形，反映了作为分子与分母的这两个无穷小趋于零的速度的“快慢”不同．就以上的几个例子来说，在x→0的时候，x2→0比2x→0的速度“快”；反过来，2x→0比x2→0的速度“慢”；而sin x→0与x→0的速度“相同”．

定义4　设α及β都是自变量同一变化过程中的无穷小，且β≠0．

（1）如果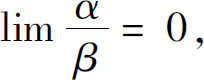则称α是比β高阶的无穷小，或称β是比α低阶的无穷小，记为α＝o（β）；

（2）如果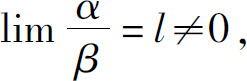则称α与β是同阶无穷小，记为α＝O（β）．特别当l＝1时，则称α与β是等价无穷小，记为α～β．

例如，sin x与x当x→0时都是无穷小，由于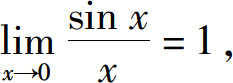所以sin x与x是当x→0时的等价无穷小，即sin x～x（x→0）．

又如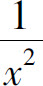，与当x→∞时都是无穷小，由于

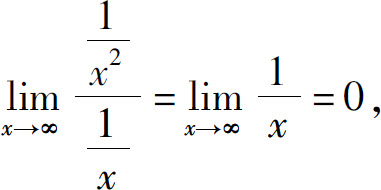
因此，当x→∞时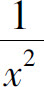是比高阶的无穷小，即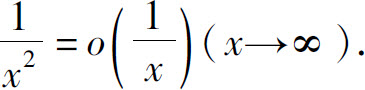

又如，x2－4与x－2都是当x→2时的无穷小．由于

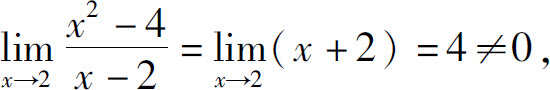
因此，x2－4与x－2为当x→2时的同阶无穷小，即x2－4＝O（x－2）（x→2）．

定理3　设α～α1，β～β1，且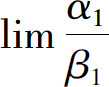存在，则

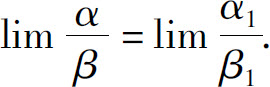
证

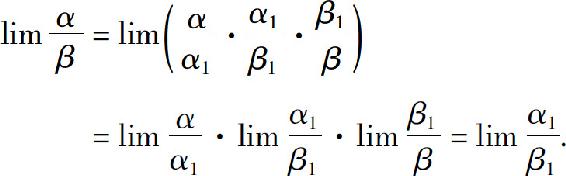
定理表明，求函数极限时，分子、分母中的因式都可用等价无穷小来代换．

例1　计算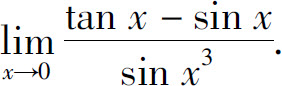

解　由于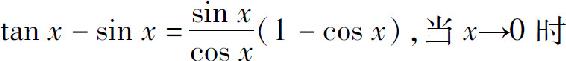

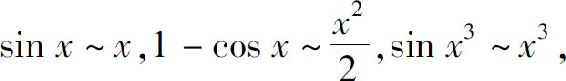
故有

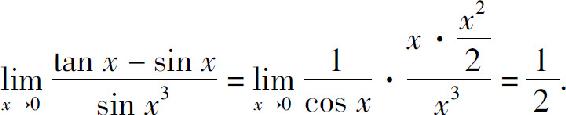
例2　计算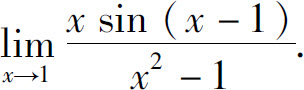

解　当x→1时，sin（x－1）～（x－1），所以

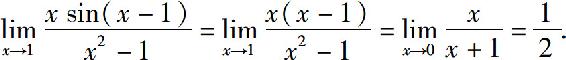
最后，我们把常用的几个x→0时的等价无穷小列出，以便于应用．

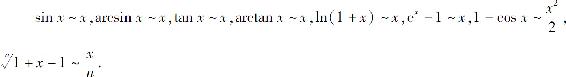
习题1.5

1．在下列各题中，指出哪些是无穷小，哪些是无穷大：

（1）

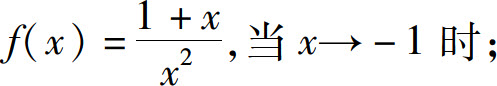
（2）

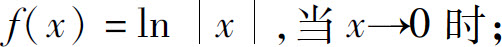
（3）

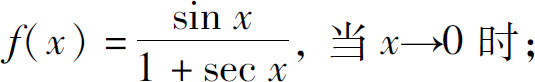
（4）

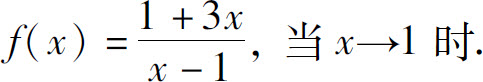
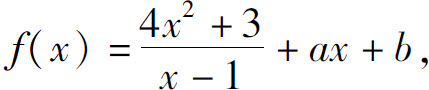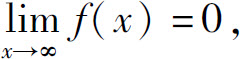2．设若已知求a，b．

3．试比较α（x）和β（x）中哪一个是高阶无穷小？

（1）α（x）＝x3＋10x，β（x）＝x4，当x→0时；

（2）α（x）＝5x3，β（x）＝sin2x，当x→0时．

4．利用等价无穷小求下列极限：

（1）

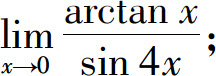
（2）

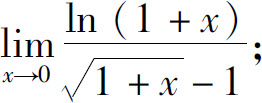
（3）