部分习题参考答案

第1章

习题1.1

1．（1）（－3，3）；

（2）（－1，＋∞）；

（3）（－∞，0）∪（0，3］；

（4）［1，5］．

2．f（0）＝－1，f（1）＝4，f（2）＝5，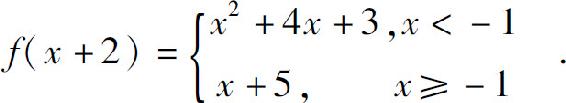

3．（1）奇函数；

（2）偶函数；

（3）偶函数；

（4）奇函数；

（5）非奇非偶；

（6）奇函数．

4．不能．

5．（1）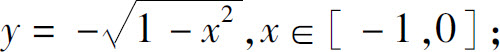

（2）

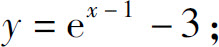
（3）

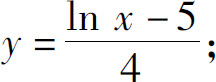
（4）

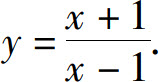
6．（1）y＝u20，u＝1＋x；

（2）y＝u2，u＝arcsin v，v＝x2；

（3）y＝ln u，u＝1＋v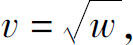，w＝1＋x2；

（4）y＝2u，u＝v2，v＝sin x．

习题1.2

2．（1）1；

（2）0；

（3）

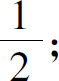
（4）1；

（5）

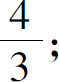
（6）

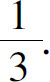
习题1.3

2．（1）－1，1；不存在

3．（1）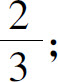

（2）

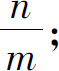
（3）

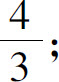
（4）

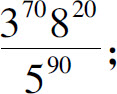
（5）－1；

（6）

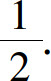
习题1.4

1．（1）4；

（2）1；

（3）0；

（4）

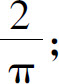
（5）sin 2a；

（6）1；

（7）－1；

（8）0．

2．（1）e4；

（2）e2；

（3）en；

（4）e2；

（5）e2；

（6）e；

（7）e；

（8）α．

3．（1）0；

（2）1．

习题1.5

1．（1）无穷小；

（2）无穷大；

（3）无穷小；

（4）无穷大．

2．a＝－4，b＝－4．

3．（1）β（x）；

（2）α（x）．

4．（1）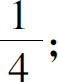

（2）2；

（3）

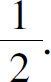
习题1.6

1．（1）x＝0，第二类间断点；

（2）x＝0，跳跃间断点；

（3）x＝0，可去间断点；

（4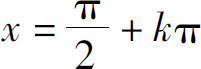）（k＝0，±1，±2，…），跳跃间断点；

（5）除x＝0外，每一点都是第二类间断点；

（6）x＝－7为第二类间断点，x＝1为跳跃间断点．

2．

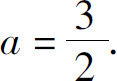
3．（1）f［g（x）］处处连续；g［f（x）］，x＝0为可去间断点；

（2）f［g（x）］，x＝－1，0，1为跳跃间断点；g［f（x）］处处连续．

4．（1）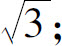

（2）1；

（3）

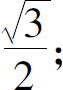
（4）0；

（5）π；

（6）e．

习题1

一、填空题

1．arcsin（1－x2）；

2．1；

3．1；

4．存在且相等；

5．－6；

6．ln 2．

二、选择题

1．A；

2．D；

3．C；

4．D；

5．B；

6．B．

三、单项解答题

1．（1）1；

（2）

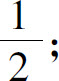
（3）e－2；

（4）2；

（5）2；

（6）e．

2．（1）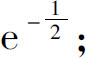

（2）2；

（3）1；

（4）1．

第2章

习题2.1

1．－4．

2．（1）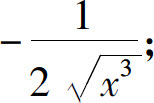

（2）－sin x．

3．切线方程：y＝1，法线方程：x＝0．

4．切线方程：x－y＝0，法线方程：x＋y－6＝0．

5．a＝4，b＝－4．

习题2.2

1．（1）x2＋x－2；

（2）

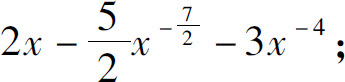
（3）2x ln x＋x；

（4）

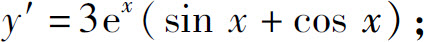
（5）

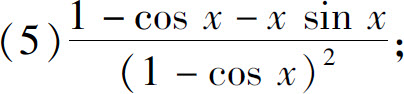
（6）

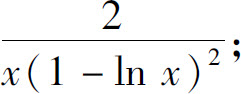
（7）

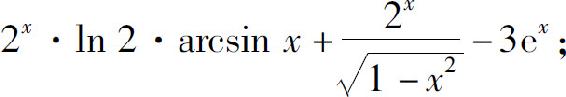
（8）x cos x＋xln x（2 cos x－x sin x）．

2．（1）10x（1＋x2）4；

（2）

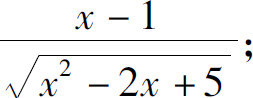
（3）

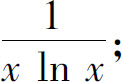
（4）

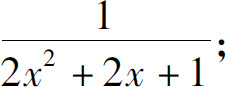
（5）

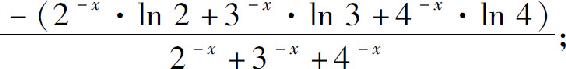
（6）

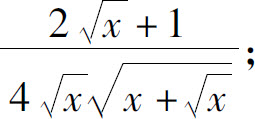
（7）

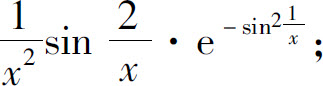
（8）

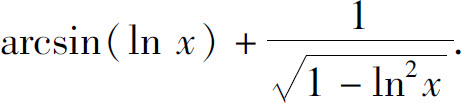
4．（1）2xf′（x2）；

（2）

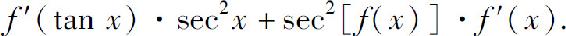
习题2.3

1．（1）6x＋4；

（2）（4x2－2）e－x2；

（3）－2 cos 2x；

（4）

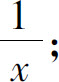
（5）

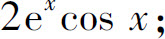
（6）

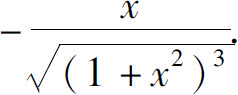
2．0．

3．（1）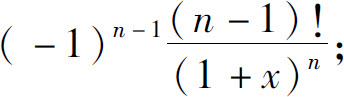

（2）

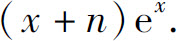
习题2.4

1．（1）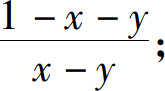

（2）

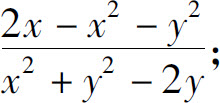
（3）

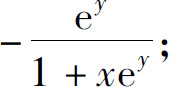
（4）

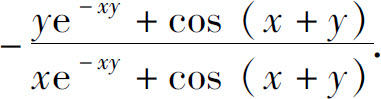
2．（1）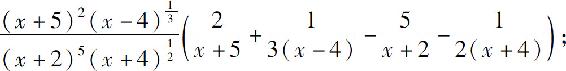

（2）

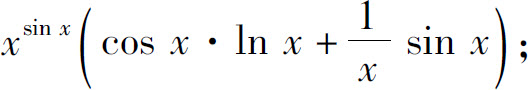
（3）

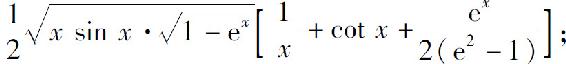
3．

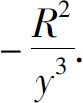
4．（1）2t2；

（2）

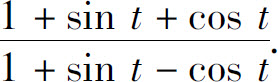
5．切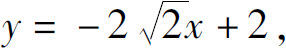线方程法线方程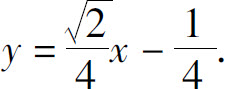

习题2.5

1．（1）－2.16；

（2）－0.025．

2．（1）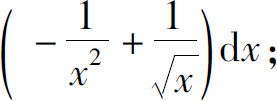

（2）ln xdx；

（3）（2x cos x－2x2 sin 2x）dx；

（4）e－x［sin（3－x）－cos（3－x）］dx；

（5）

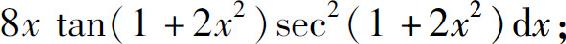
（6）

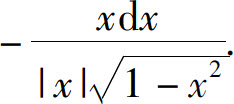
3．（1）1.0067；

（2）0.002．

习题2

一、填空题

1．2f′（x0）．

2．y＝x－e．

3．a＝2，b＝－1．

4．

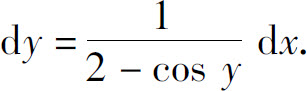
5．f′（0）．

二、单项选择题

1．B．

2．B．

3．C．

4．D．

5．D．

三、解答题

1．（1）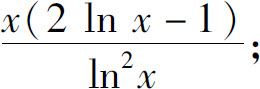

（2）

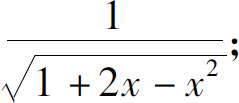
（3）

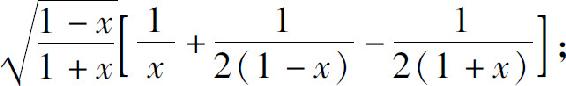
（4）2 lnx·xln x－1；

2．

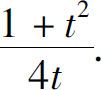
3．

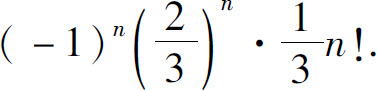
第3章

习题3.1

2．有分别位于区间（0，1），（1，2），（2，3）内的三个根．

9．提示：令φ（x）＝f（x）e－x，先证明φ（x）为常数．

习题3.2

1．（1）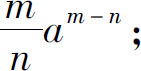

（2）

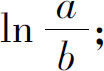
（3）1；

（4）2；

（5）

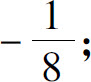
（6）

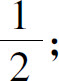
（7）1；

（8）3；

（9）2；

（10）1；

（11）

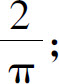
（12）

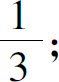
（13）∞；

（14）

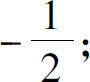
（15）

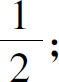
（16）

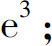
（17）1；

（18）1；

（19）

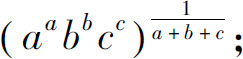
（20）

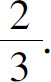
习题3.3

1．在（－∞，＋∞）上单调减少．

3．（1）在（－∞，＋∞）上单调增加；

（2）在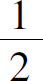［，＋∞）上单调增加，在（0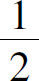，］上单调减少；

（3）在（－∞，1］和［3，＋∞）上单调增加，在［－1，3］上单调减少；

（4）在［2，＋∞）上单调增加，在（0，2］上单调减少；

（5）在（－∞，－2］和［0，＋∞）上单调增加，在［－2，0］上单调减少；

（6）在（－∞，＋∞）上单调增加；

（7）在（－∞，－2）和（8，＋∞）上单调增加，在（－2，8）上单调减少；

（8）在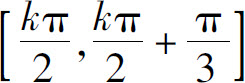上单调增加；

在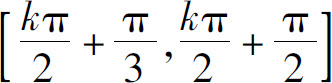上单调减少（k＝0，±1，±2，…）．

6．（1）极小值y（1）＝4；

（2）极大值y（0）＝0，极小值y（1）＝－1；

（3）极大值y（－1）＝10，极小值y（3）＝－54；

（4）极小值y（0）＝0；

（5）无极值；

（6）极大值y（±1）＝7，极小值y（0）＝6；

（7）极大值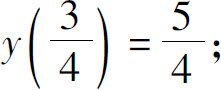

（8）极大值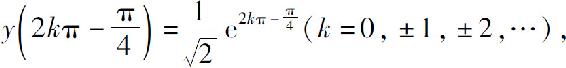

极小值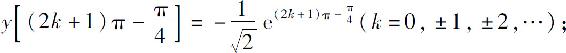

（9）极大值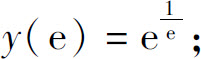

（10）极大值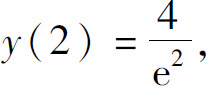极小值y（0）＝0；

（11）极大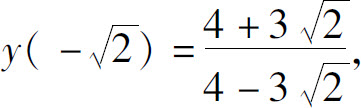值极小值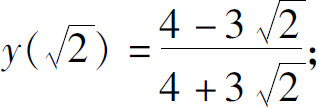

（12）极小值y（0）＝2；

（13）极大值y（－1）＝2；

（14）无极值；

（15）极大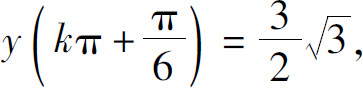值极小值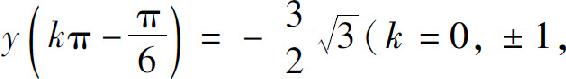

（16）无极值．

7．a＝2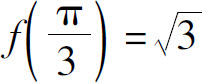，为极大值．

8．（1）最大值y（4）＝0，最小值y（－1）＝－85；

（2）最大值y（3）＝9，最小值y（2）＝－16；

（3）最大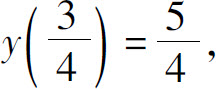值最小值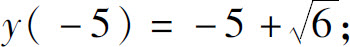

（4）最大值y（0）＝0，最小值y（－1）＝－2．

9．（1）x＝－3时函数有最小值27；

（2）没有最大，最小值；

（3）x＝1时函数有最大值．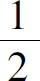

10．a≥2时最近距离为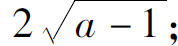a＜2时最近距离为｜a｜．

11．底半径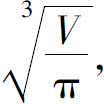为高为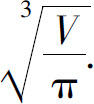

12．当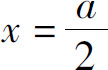反应速度最大．

13．

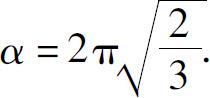
14．每小时57 km，总费用为82.2元．

习题3.4

1．（1）凸区间（－∞，＋∞）；

（2）凹区间（0，＋∞）；

（3）凸区间（－∞，2］，凹区间［2，＋∞），拐点（2，－10）；

（4）凸区间（－∞，2］，凹区间［2，＋∞）；拐点（2，2e－2）；

（5）凹区间（－∞，＋∞）；

2．a＝－3，拐点为（1，－7），凸区间为（－∞，1］，凹区间为（1，＋∞）．

3．

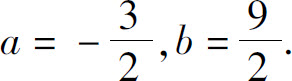
4．（1）y＝0；

（2）y＝0，x＝－1，x＝1；

（3）y＝x－3，x＝－1．

习题3.5

1．K＝2．

2．K＝｜cos x｜，ρ＝｜sec x｜．

3．K＝2，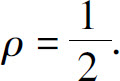

4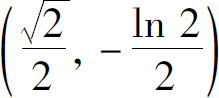．处曲率半径有最小值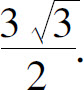

5．

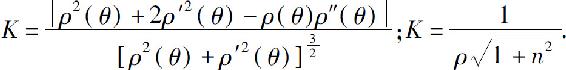
习题3.6

1．2．

2．

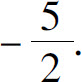
习题3

一、填空题

1．［－1，1］．

2．1．

3．a＝1，b＝－3．

4．

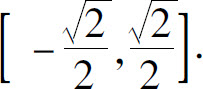
5．1．

6．

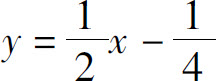
二、单项选择题

1．A．

2．A．

3．C．

4．A．

5．D．

6．B．

7．B．

8．A．

9．B．

三、解答题

1．（1）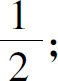

（2）0；

（3）

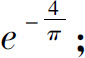
（4）1；

（5）100！；

（6）

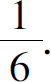
4．当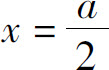时有最大面积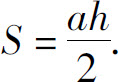

5．（1）有且仅有一个实根；

（2）至少有一个实根．

9．点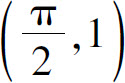处曲率半径有最小值1．

第4章

习题4.1

1．F（x2）．

2．y＝1＋ln x．

3．（1）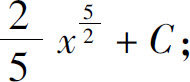

（2）

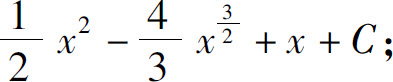
（3）

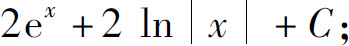
（4）

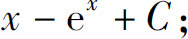
（5）

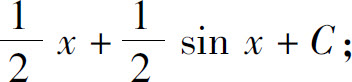
（6）2 sin x＋C；

（7）

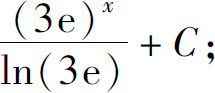
（8）

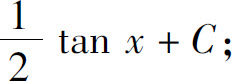
（9）

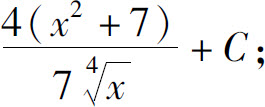
（10）

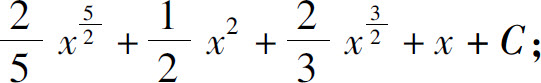
（11）x－arctan x＋C；

（12）2arcsin x－arctan x＋C；

（13）

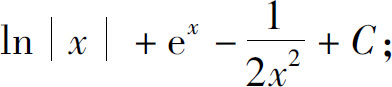
（14）

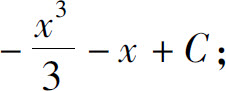
（15）

（16）

（17）

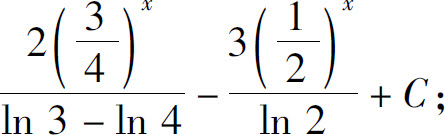
（18）－cot x－x＋C；

（19）－csc x＋cot x＋C；

（20）－（tan x＋cot x）＋C；

（21）

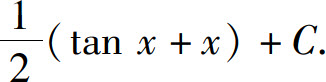
习题4.2

1．（1）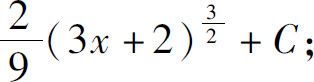

（2）

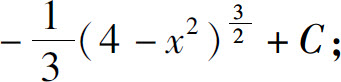
（3）

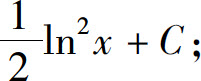
（4）

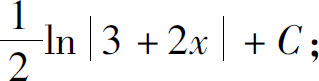
（5）

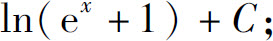
（6）

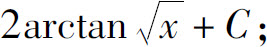
（7）

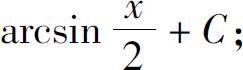
（8）

（9）

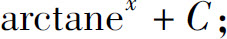
（10）

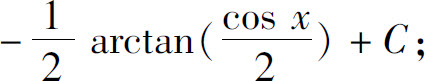
（11）

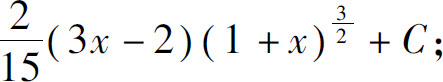
（12）

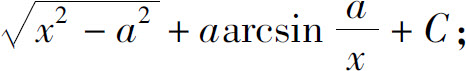
（13）

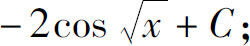
（14）ln｜tan x｜＋C；

（15）

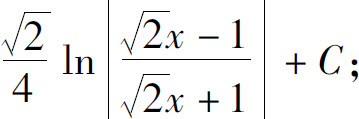
（16）

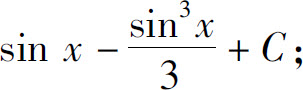
（17）

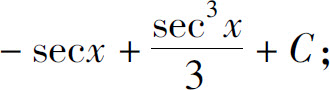
（18）

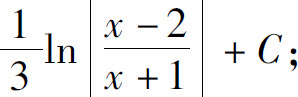
（19）

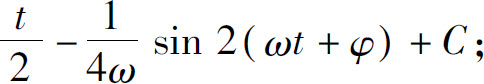
（20）

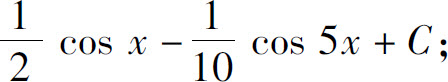
（21）

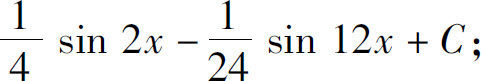
（22）

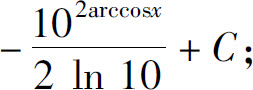
（23）

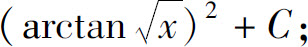
（24）

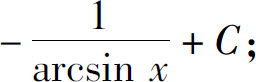
（25）

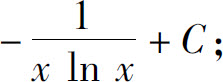
（26）

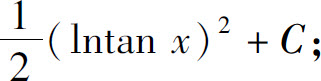
（27）

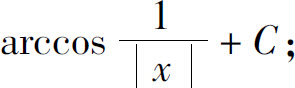
（28）

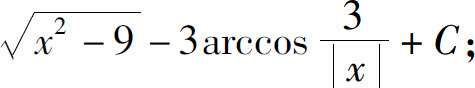
（29）

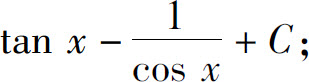
（30）

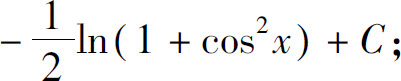
（31）

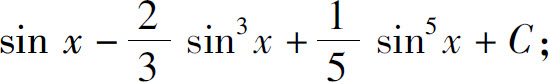
（32）

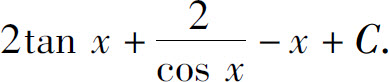
2．（1）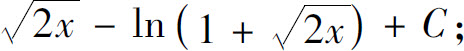

（2）

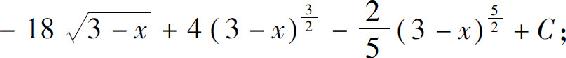
（3）

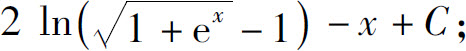
（4）

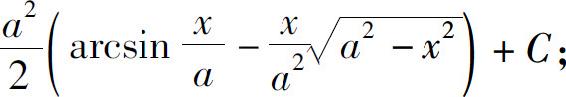
（5）

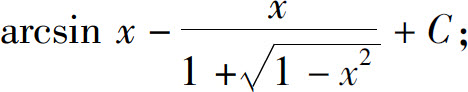
（6）

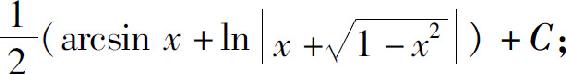
（7）

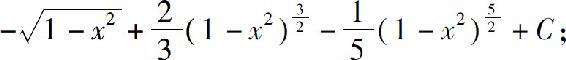
（8）

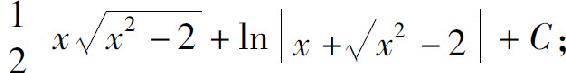
（9）

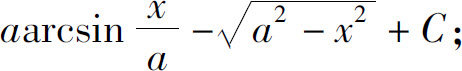
（10）

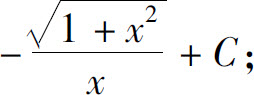
（11）

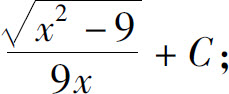
（12）

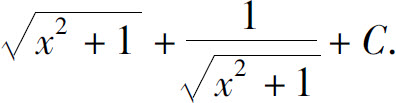
习题4.3

1．（1）－x cos x＋sin x＋C；

（2）

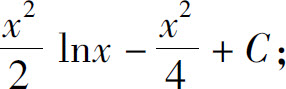
（3）x ln（1＋x2）－2x＋2 arctan x＋C；

（4）－e－x x2＋2x＋2＋C；

（5）

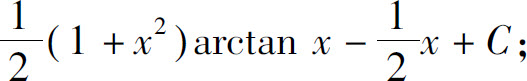
（6）

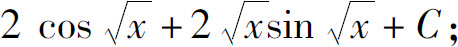
（7）

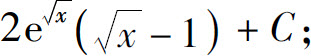
（8）

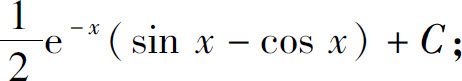
（9）

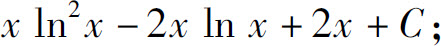
（10）

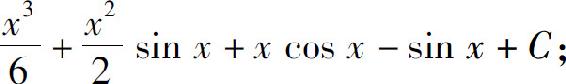
（11）

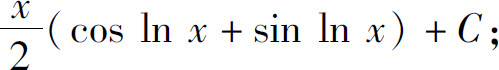
（12）

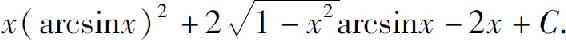
2．

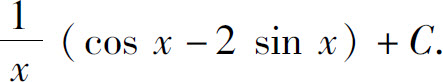
习题4.4

1．ln｜x2＋3x－10｜＋C．

2．

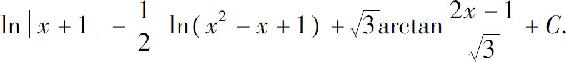
3．

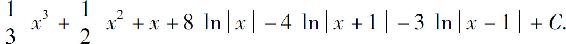
4．

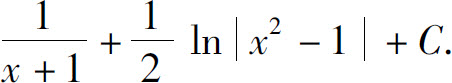
5．

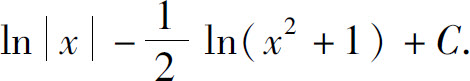
6．

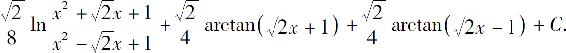
7．

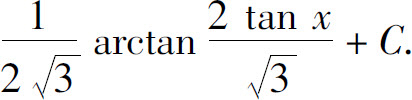
8．

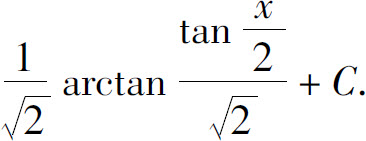
9．

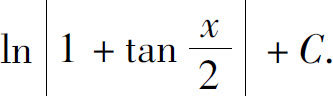
10．

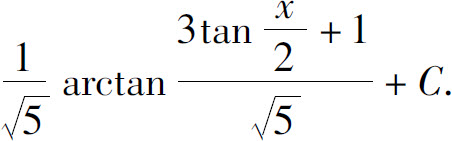
习题4

一、填空题

1．f（x）＋C．

2．

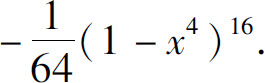
3．G（x）＝F（x）＋C．

4．

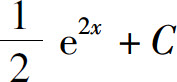
5．

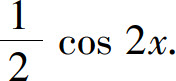
二、单项选择题

1．B．

2．B．

3．D．

4．C．

5．D．

三、解答题

（1）

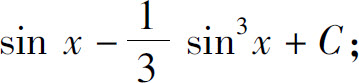
（2）

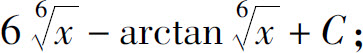
（3）

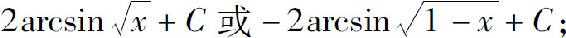
（4）

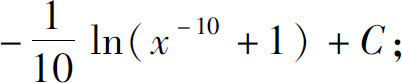
（5）

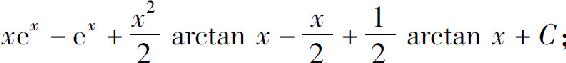
（6）

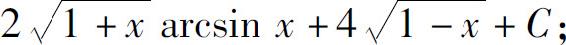
（7）

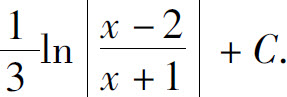
第5章

习题5.1

1．

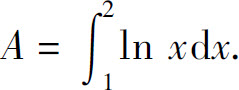
2．（1）1；

（2）

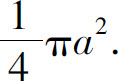
3．（1）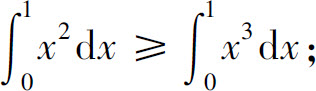

（2）

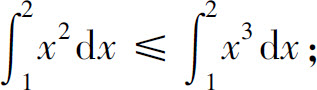
（3）

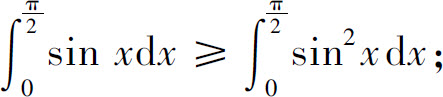
（4）

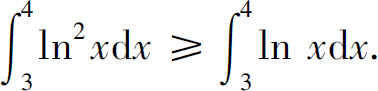
4．（1）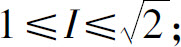

（2）

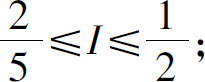
（3）π≤I≤2π；

（4）

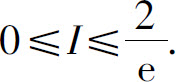
习题5.2

1．（1）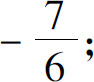

（2）

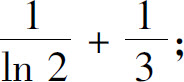
（3）

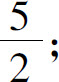
（4）

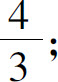
（5）

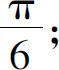
（6）

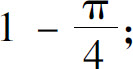
（7）

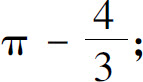
（8）

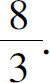
2．（1）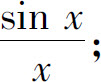

（2）

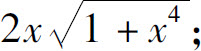
（3）

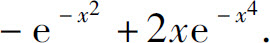
3．

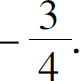
4．2．

5．

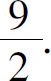
习题5.3

1．（1）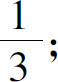

（2）

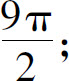
（3）

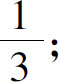
（4）

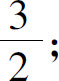
（5）

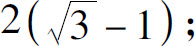
（6）

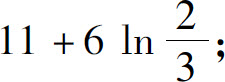
（7）

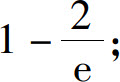
（8）1；

（9）

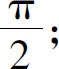
（10）

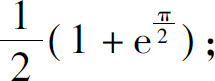
（11）

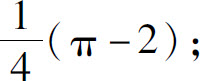
（12）1．

2．8．

习题5.4

1．（1）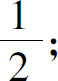

（2）发散；

（3）

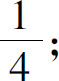
（4）

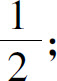
（5）π；

（6）1；

（7）发散；

（8）

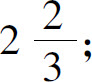
（9）

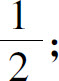
（10）

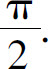
2．当k＞1时收敛于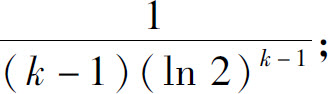当k≤1时发散；当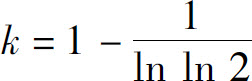时取得最小值．

习题5.5

1．（1）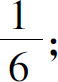

（2）1；

（3）

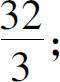
（4）

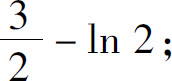
（5）e＋e－1－2；

（6）

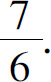
2．

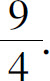
3．（1）πa2；

（2）

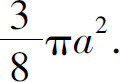
4．（1）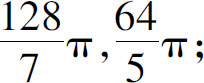

（2）

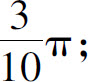
5．

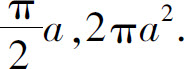
6．5000π kgm．

7．14373.33 kN．

8．水平方向分力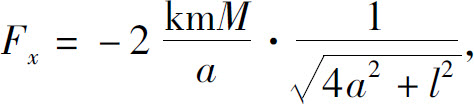：垂直方向分力：Fy＝0．

9．q（p）＝20 ln（p＋1）＋1000．

10．

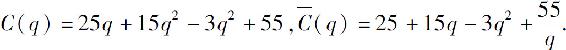
11．R（q）＝3q－0.1q2，当q＝15时收入最高为22.5．

12．（1）9987.5；

（2）19850．

习题5

一、填空题

1．0．

2．

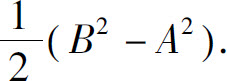
3．收敛．

4．

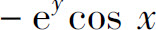
5．0．

6．π．

7．1．

8．π［g（y）］2 dy．

二、单项选择题

1．D．

2．B．

3．D．

4．A．

5．C．

6．C．

7．A．

8．B．

9．A．

三、解答题

1．（1）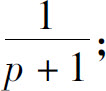

（2）

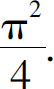
2．（1）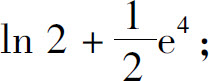

（2）

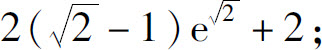
（3）

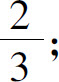
（4）

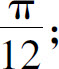
（5）

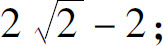
（6）

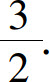
3．b－a．

4．（1）3π；

（2）5π2．

5．

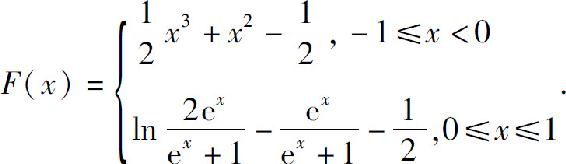
6．（1）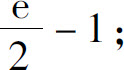

（2）

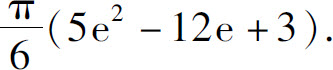
第6章

习题6.1

1．

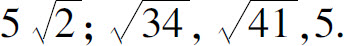
2．（1，0，0）．

3．x＋2y－3z－2＝0．

5．（1）｛（x．y）｜x≥y｝；

（2）｛（x．y）｜xy≥0｝；

（3）｛（x，y）｜y≥x2且x＋y≤2｝；

（4）｛（x，y）｜y2＞4x－8｝；

（5）｛（x，y）｜｜x｜≠｜y｜｝；

（6）｛（x，y）｜｜x｜≥｜y｜且x≠0｝；

（7）｛（x，y）｜x＞0，y＞0，z＞0｝；

（8）｛（x，y）｜r2≤x2＋y2＋z2≤R2｝．

6．（1）31；

（2）（x＋y）3－2（x2－y2）＋3（x－y）2．

习题6.2

1．（1）2；

（2）2；

（3）ln 2；

（4）0；

（5）2；

（6）0；

（7）2；

（8）－2

2．不连续，不连续，连续．

3．（1）不存在；

（2）不存在．

习题6.3

1．（1）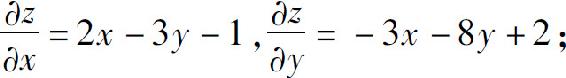

（2）

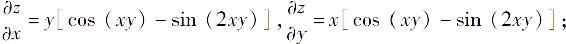
（3）

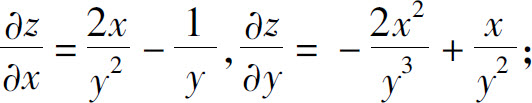
（4）

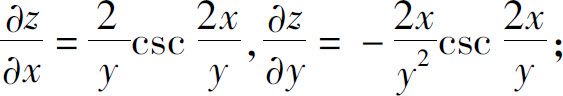
（5）

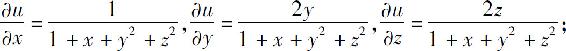
（6）

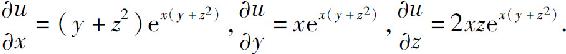
2．36，－2．

3．（1）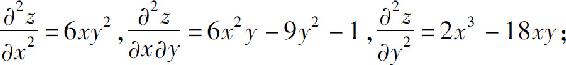

（2）

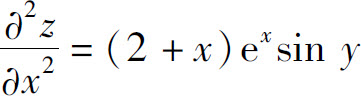
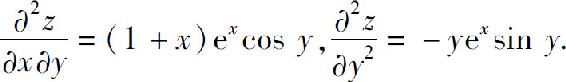
4．2，2，0．

5．

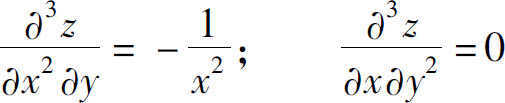
6．（1）dz＝2xydx＋（x2＋2y）dy；

（2）

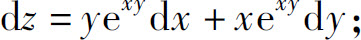
（3）

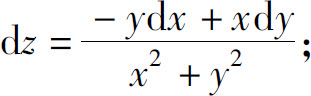
（4）

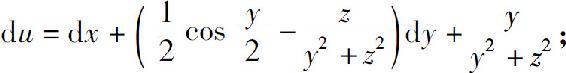
（5）dz＝0.04；

（6）

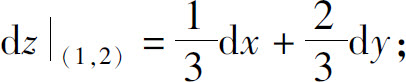
（7）

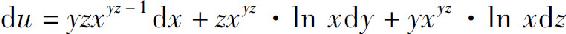
7．（1）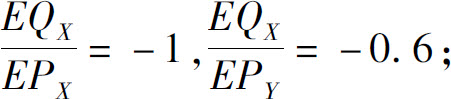

（2）0.75．

习题6.4

1．（1）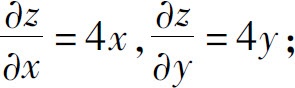

（2）

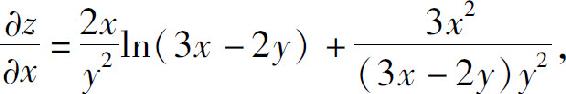
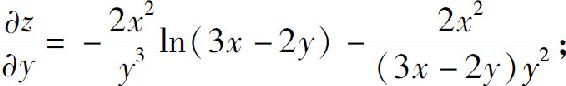
（3）

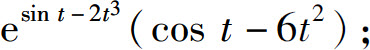
（4）

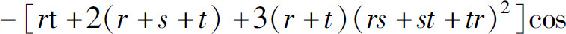
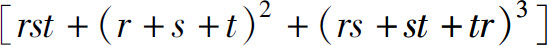
（5）

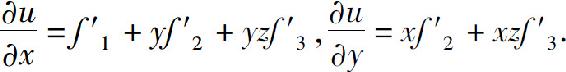
3．（1）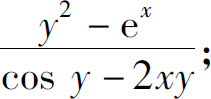

（2）

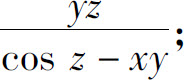
（3）

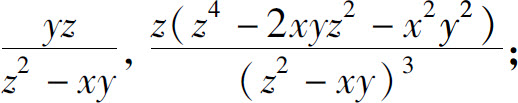
（4）

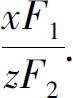
5．

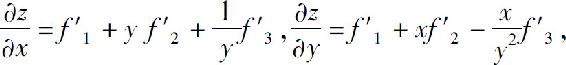
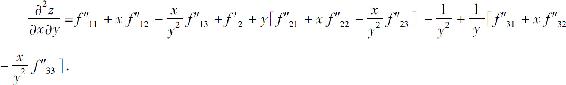
习题6.5

1．（1）极大值f（2，－2）＝8；

（2）极大值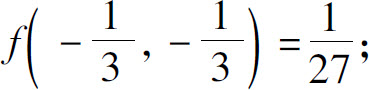

（3）极小值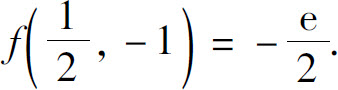

2．（1）条件极值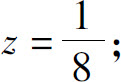

（2）条件极值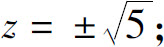

（3）条件极值u＝9．

3．

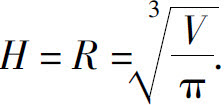
4．

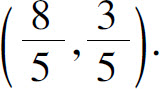
5．长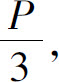为宽为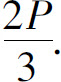

6．最大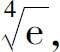值最小值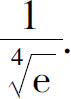

7．（1）用0.75万元作电台广告，用1.25万元作报纸广告；

（2）将1.5万元广告费全部用于报纸广告．

习题6.6

1．

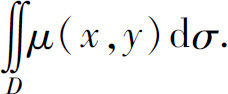
2．（1）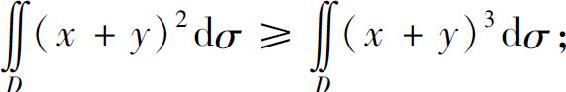

（2）

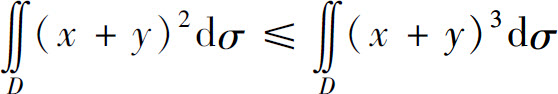
（3）

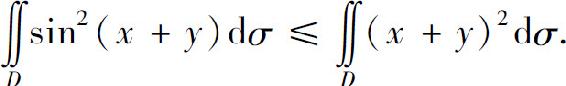
3．（1）0≤I≤2；

（2）0≤I≤π2．

4．（1）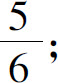

（2）

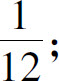
（3）－2；

（4）e－e－1．

5．（1）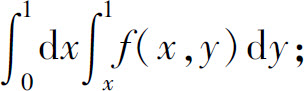

（2）

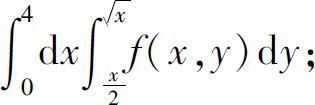
（3）

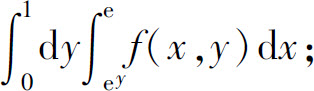
（4）

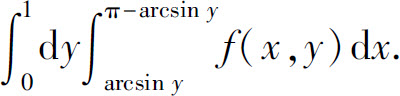
6．（1）π ln 2；

（2）

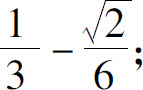
（3）18π；

（4）

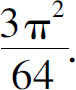
7．（1）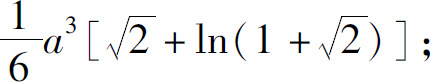

（2）

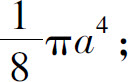
（3）

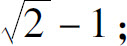
（4）

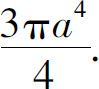
8．（1）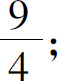

（2）

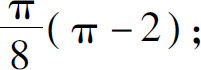
（3）14a4；

（4）

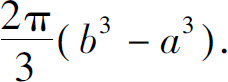
9．

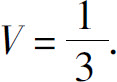
10．

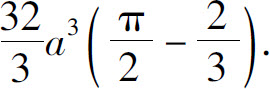
习题6

一、填空题

1．

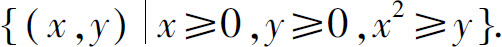
2．

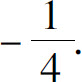
3．

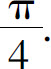
4．

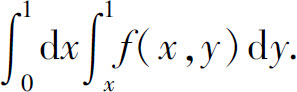
5．2π．

6．

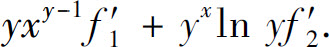
二、单项选择题

1．D．

2．A．

3．D．

4．B．

5．D．

6．B．

三、解答题

1．

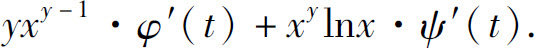
2．（1）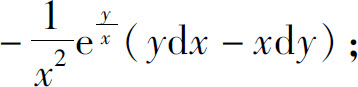

（2）

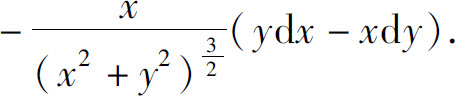
3．

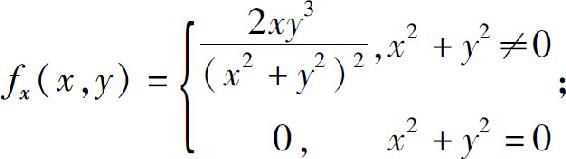
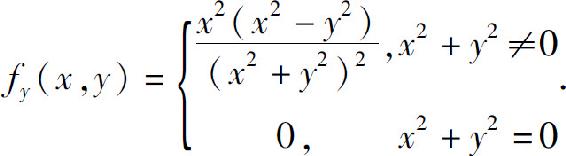
4．柱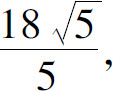高锥高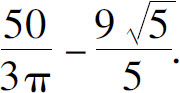

5．最大值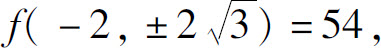最小值f（1，0）＝0．

7．（1）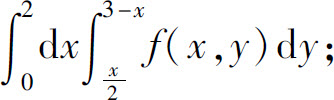

（2）

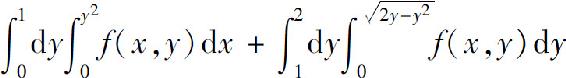
8．

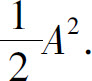
9．e－1

10．

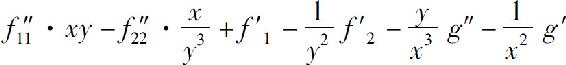
第7章

习题7.1

1．（1）一阶；

（2）二阶；

（3）一阶；

（4）二阶．

2．（1）是；

（2）不是；

（3）是；

（4）是．

3．（1）y′＝x2；

（2）xy′＝2y

4．y＝－xe－x－e－x＋1．

习题7.2

1．（1）y＝sin（x＋C）；

（2）

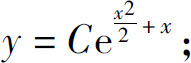
（3）y＝C sin x－3；

（4）（x－4）y4＝Cx；

（5）

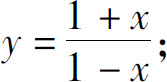
（6）y＝2（1＋x2）．

2．（1）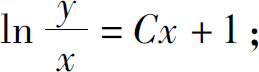

（2）

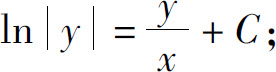
（3）x＋3y＋2 ln｜x＋y－2｜＝C；

（4）y3＝y2－x2

3．（1）y＝Cecos x；

（2）y＝cos x（C－2 cos x）；

（3）

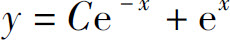
（4）

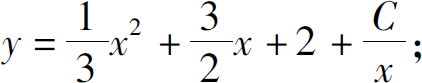
（5）

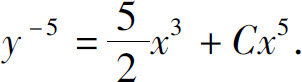
4．

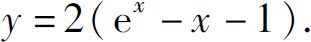
5．

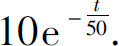
习题7.3

1．（1）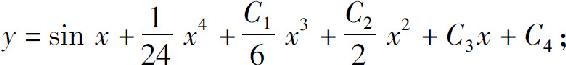

（2）

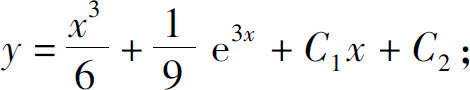
（3）

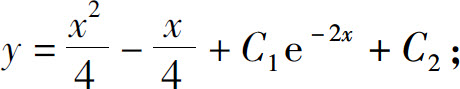
（4）

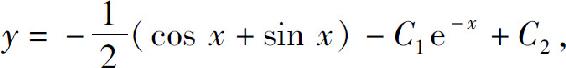
（5）y＝C1（sin x＋C2）；

（6）y2＝C1x＋C2．

2．（1）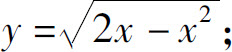

（2）

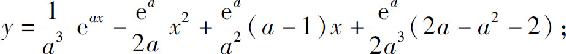
（3）y＝ln ch x．

3．

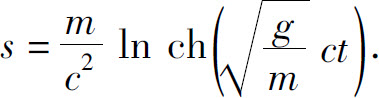
习题7.4

1．（1）线性无关；

（2）线性相关；

（3）线性无关；

（4）线性无关；

（5）线性无关；

（6）线性无关．

2．y＝C1 cos 2x＋C2 sin 2x．

习题7.5

1．（1）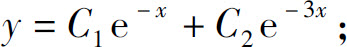

（2）

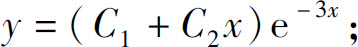
（3）

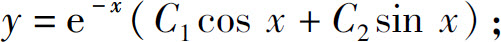
（4）

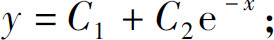
2．（1）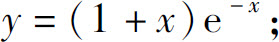

（2）

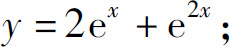
（3）

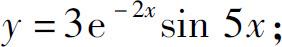
（4）

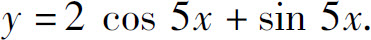
3．

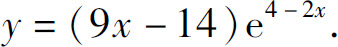
4．（1）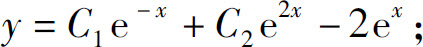

（2）

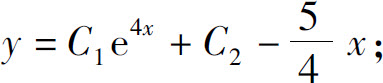
（3）

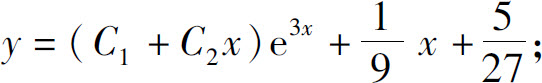
（4）

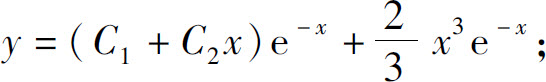
（5）

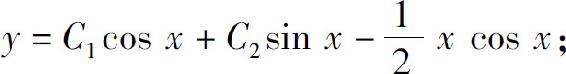
（6）

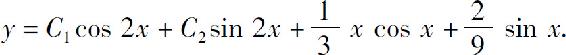
5．（1）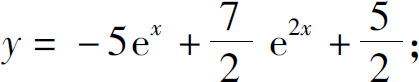

（2）

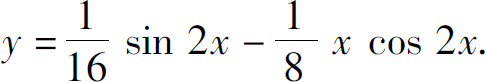
6．

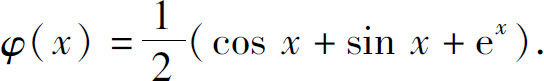
习题7.6

1．（1）一阶差分Δyx＝（n＋1）x（x－1）（x－2）…（x－n＋1），

二阶差分Δ2yx＝n（n＋1）x（x－1）（x－2）…（x－n＋2）；

（2）一阶差分Δyx＝8・32x，二阶差分Δ2yx＝64・32x；

2．（1）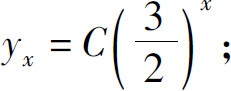

（2）yx＝C（－1）x；

（3）

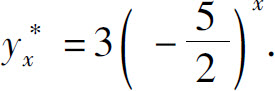
3．（1）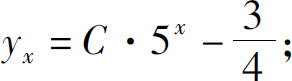

（2）

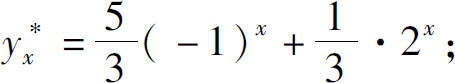
（3）

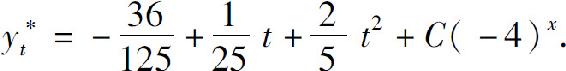
习题7

一、填空题

1．

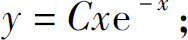
2．

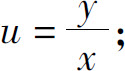
3．

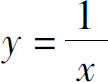
4．

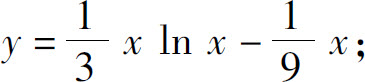
5．

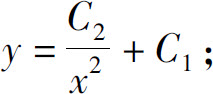
6．

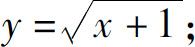
7．

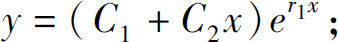
8．y″－2y′＋2y＝0；

9．b＝－4，c＝5；

10．

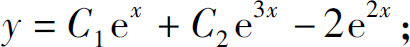
11．y＝C1（x－1）＋C2（x2－1）＋1．

二、单项选择题

1．C．

2．A．

3．A．

4．A．

5．D

6．A．

7．C．

三、解答题

1．（1）y2（1＋y′2）＝1；

（2）y″－3y′＋2y＝0．

2．（1）y＝x（ln Cx）2；

（2）

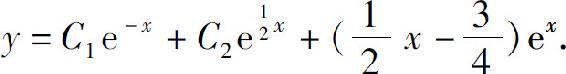
（3）

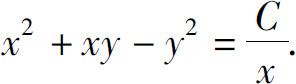
3．（1）y＝－ln（x＋1）；

（2）

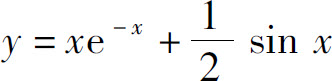
（3）

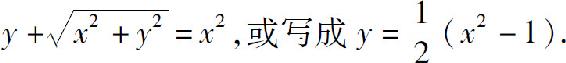
4．φ（x）＝sin x＋cos x．

5．

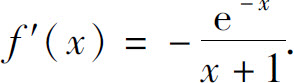
6．y＝ex．

7．1.05 km．

第8章

习题8.1

1．（1）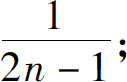

（2）

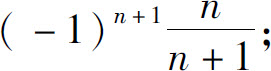
（3）

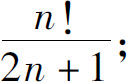
（4）

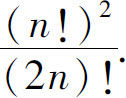
2．（1）发散；

（2）收敛．

3．（1）发散；

（2）发散；

（3）收敛；

（4）发散．

4．（1）1；

（2）3；

（3）1．

习题8.2

1．（1）发散；

（2）收敛；

（3）收敛；

（4）a＞1时收敛，a≤1时发散；

（5）收敛；

（6）发散．

2．（1）收敛；

（2）收敛；

（3）收敛；

（4）发散．

3．（1）收敛；

（2）收敛；

（3）收敛；

（4）收敛．

4．（1）发散；

（2）收敛；

（3）发散；

（4）收敛．

习题8.3

1．（1）收敛；

（2）收敛；

（3）收敛；

（4）发散．

2．（1）条件收敛；

（2）条件收敛；

（3）绝对收敛；

（4）绝对收敛；

（5）发散；

（6）绝对收敛．

3．

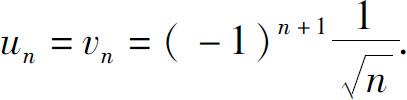
习题8.4

1．（1）（－1，1）；

（2）

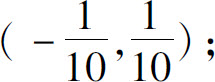
（3）（－1，1］；

（4）［－1，1］；

（5）（－1，1］；

（6）［4，6）；

（7）［－1，5）．

2．（1）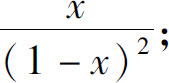

（2）

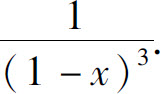
习题8.5

1．（1）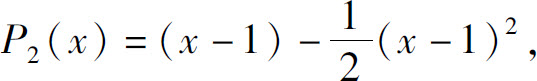

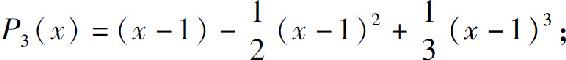
（2）

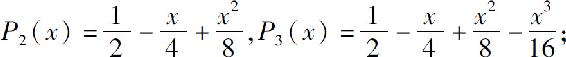
（3）

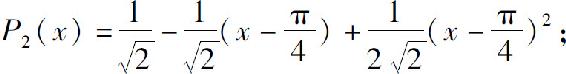
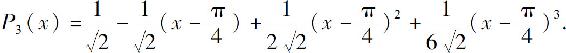
2．（1）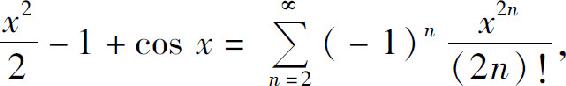

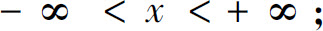
（2）

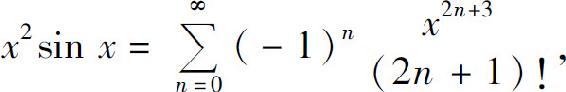
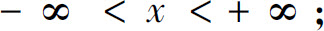
（3）

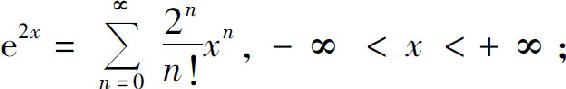
（4）

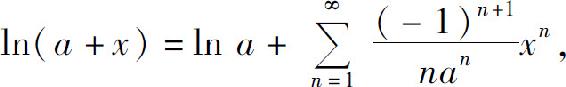
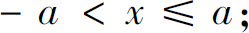
（5）

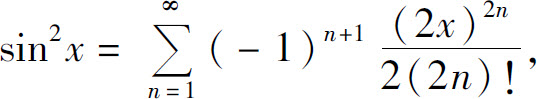
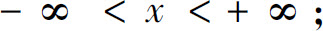
（6）

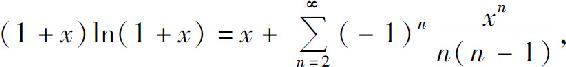
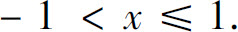
3．

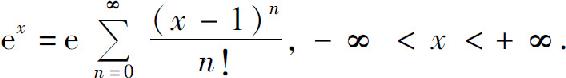
4．

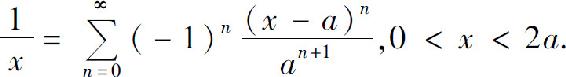
习题8.6

1．（1）0.6931，提示：应用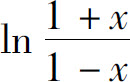的幂级数展开式；

（2）1.648；

（3）2.9926．

2．（1）0.5205；

（2）0.4940．

3．（1）；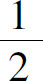

（2）．

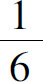4．（1）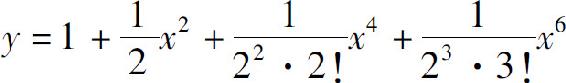

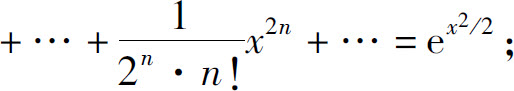
（2）

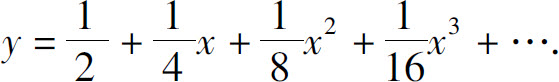
习题8

一、填空题

1．0．

2．＞1．

3．充分必要．

4．（－2，2）．

5．［0，6］．

6．（1，5］．

7．（－2，4）．

8．

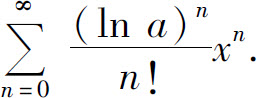
二、单项选择题

1．B．

2．A．

3．C．

4．D．

5．D．

6．B

三、解答题

1．当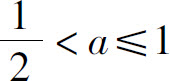时，级数发散；当a＞1时，级数收敛．

2．（1）收敛且绝对收敛；

（2）条件收敛．

3．收敛区间为（－3，3），x＝3时级数发散，x＝－3时收敛．

4．收敛域为（－2，2），和函数为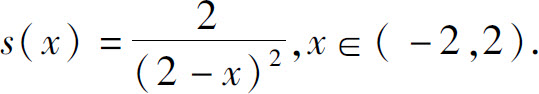

5．

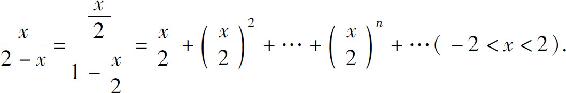
6．

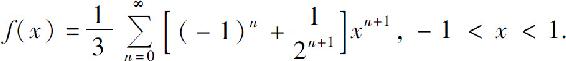
7．

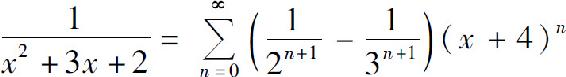
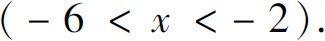
8．