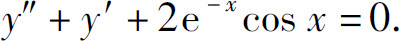2.3　高阶导数

2.3　高阶导数

如果函数y＝f（x）的导函数f′（x）仍可导，则称f′（x）的导数为f（x）的二阶导数，记为

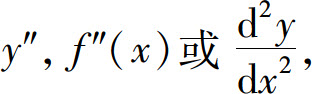
即

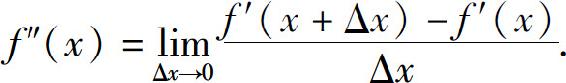
同时称f（x）二阶可导．相应地称f′（x）为f（x）的一阶导数．

一般地，可由f（x）的n－1阶导函数定义f（x）的n阶导数，记为

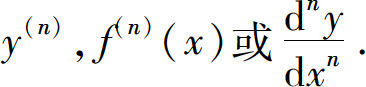
这里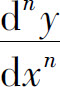也可写作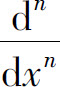y，它是对y相继进行n次求导运算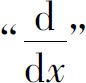的结果．

二阶以及二阶以上的导数都称为高阶导数．

例1　求y＝xk（k为正整数）的n阶导数．

解

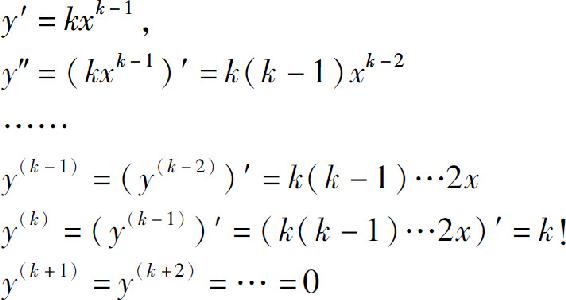
因此

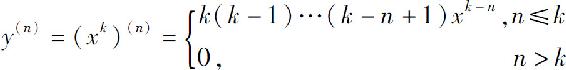
例2　求y＝sin x的n阶导数．

解　注意诱导公式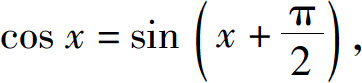则有

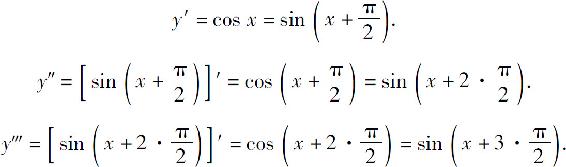
一般地

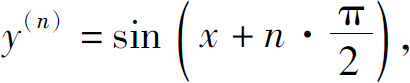
即

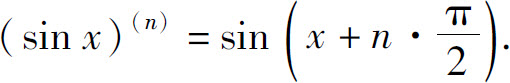
类似可得：

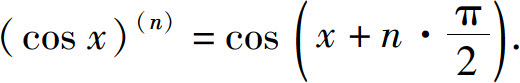
求函数的高阶导数常用到以下两个公式：

如果u（x），v（x）有直到n阶的导数，则

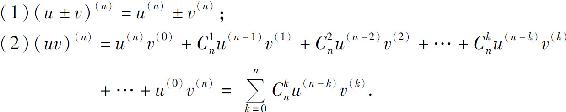
其中，u（0）＝u，v（0）＝v．公式（2）可以用数学归纳法证明，其形式与二项式（u＋v）n展开式相似，称为莱布尼茨公式．

例3　设y＝x3e－x，求y（30）．

解　由例1可知

（x3）（k）＝0，（k＞3）．

因此由莱布尼茨公式得

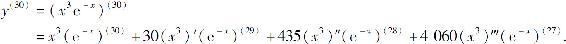
又由于

（e－x）（n）＝（－1）ne－x，

因此

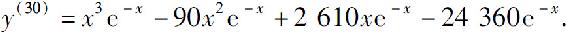
习题2.3

1．求下列函数的二阶导数：

（1）y＝x3＋2x2＋1；

（2）

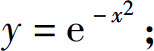
（3）

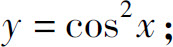
（4）y＝x ln x；

（5）

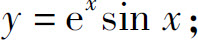
（6）

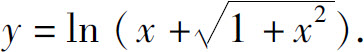
2．设函数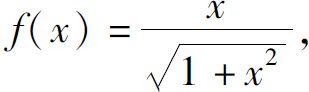求f″（0）．

3．求下列函数的n阶导数：

（1）y＝ln（1＋x）；

（2）

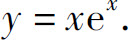
4．证明：y＝e－x（sin x＋cos x）满足方程：