习题5

习题5

一、填空题

1．设函数f（x）在［a，b］上连续，则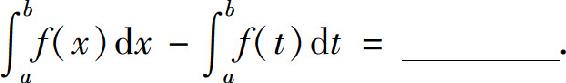

2．设函数f（x）在［a，b］上可导，且f（a）＝A，f（b）＝B，则_____．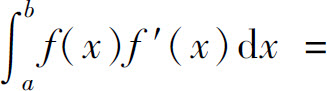

3．设在［a，＋∞）上f（x）≥0，对任意A＞a，f（x）在［a，A］上可积，且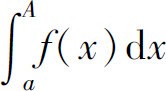有界，则无穷积分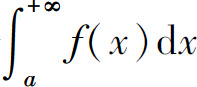一定_____．

4．设y＝f（x）由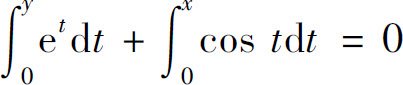确定，则f′（x）＝_____．

5．当x＝_____时，函数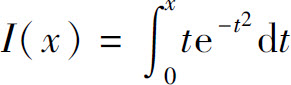有极值．

6．位于曲线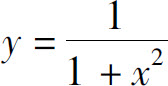下方，x轴上方的无界图形的面积为_____．

7．曲线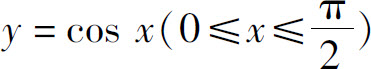与x轴、y轴所围图形的面积为_____．

8．设旋转体由曲线x＝g（y），直线y＝c，y＝d（c＜d）及y轴所围成的曲边梯形绕y轴旋转一周而成，则其体积元素dV＝_____．

二、单项选择题

1．设f（x）是连续的偶函数，a＞0，则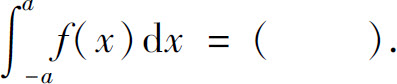

A．0
B．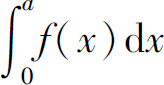
C．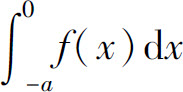
D．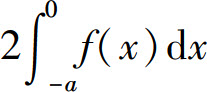

2．设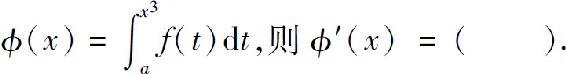

A．f（x）
B．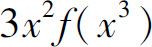
C．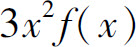
D．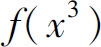

3．由对称性，积分（　）为零．

A．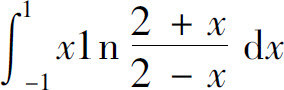
B．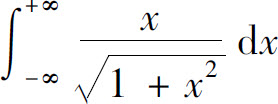
C．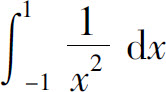
D．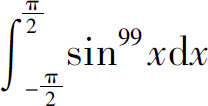

4．若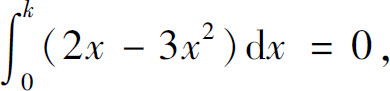dx＝0，则k＝（　）．

A．0或1
B．1
C．－1
D．0

5．设f（x）连续，则下列各式正确的是（　）．

A．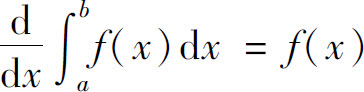
B．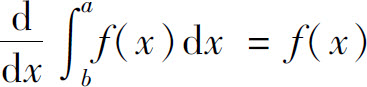
C．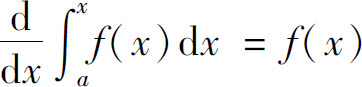
D．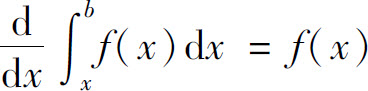

6．无穷积分（　）收敛．

A．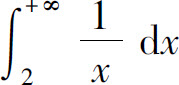
B．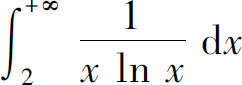
C．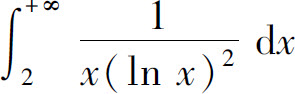
D．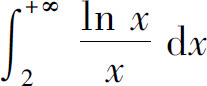

7．曲线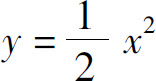与上半圆x2＋y2＝8（y≥0）所围图形的面积为（　）．

A．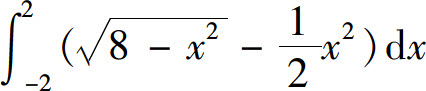
B．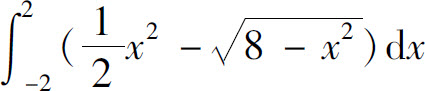
C．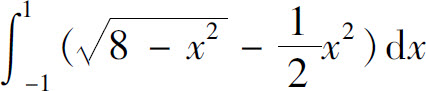
D．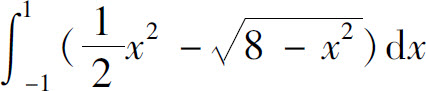

8．设函数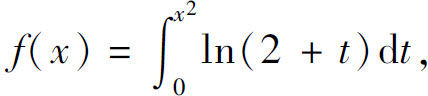则f′（x）的零点个数为（　）．

A．0
B．1
C．2
D．3

9．设f（x）连续，则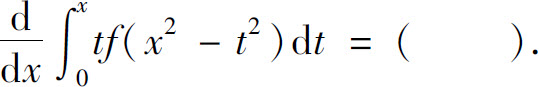

A．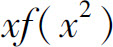
B．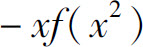
C．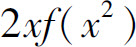
D．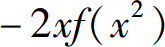

三、解答题

1．求下列极限：

（1）

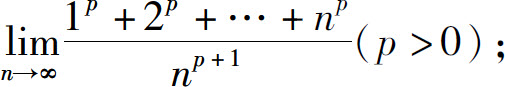
（2）

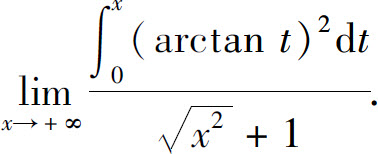
2．计算下列积分：

（1）

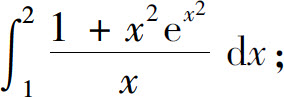
（2）

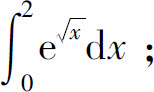
（3）

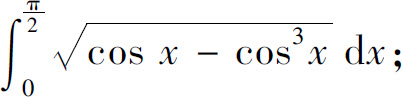
（4）

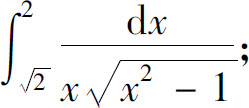
（5）

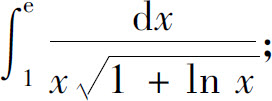
（6）

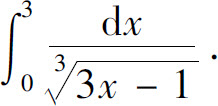
3．求由曲线y＝ln x，y轴与直线y＝ln a，y＝ln b（b＞a＞0）围成的平面图形的面积．

4．已知平面图形由摆线x＝t－sin t，y＝1－cos t的一拱（0≤t≤2π）与x轴围成，求

（1）图形的面积；

（2）图形绕x轴旋转所成旋转体的体积．

5．设

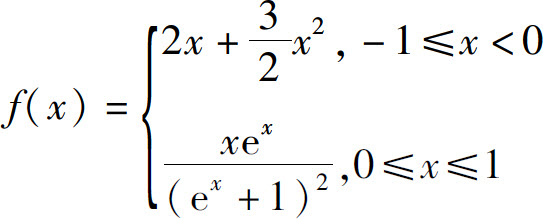
求函数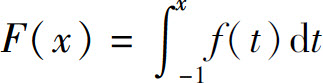的表达式．

6．过坐标原点作曲线y＝ln x的切线，该切线与曲线y＝ln x及x轴围成平面图形D．

（1）求D的面积A；

（2）求绕直线x＝e旋转一周所得旋转体的体积V．