习题1

习题1

一、填空题

1．已知f（x）＝sin x，f［φ（x）］＝1－x2，则φ（x）＝_____．

2．设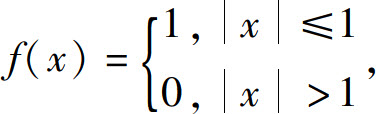，则f［f（x）］＝_____．

3．设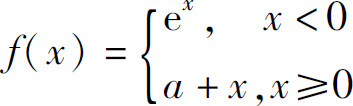在（－∞，＋∞）内连续，则a＝_____．

4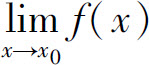．存在的充分必要条件是_____．

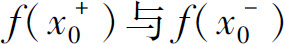5．设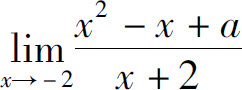存在，则a＝_____．

6．设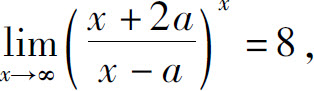，则a＝_____．

二、单项选择题

1．下列各对函数相同的是（　）．

A．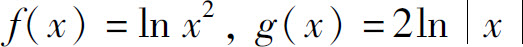
B．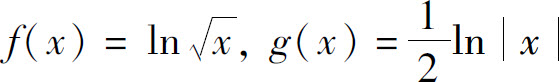
C．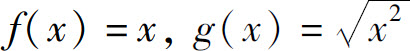
D．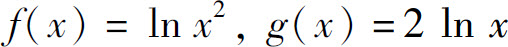

2．数列｛xn｝与｛yn｝的极限分别为A和B，且A≠B．数列x1，y1，x2，y2，…的极限为（　）．

A．A
B．B
C．A＋B
D．不存在

3．当x→0＋时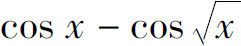，是x的（　）．

A．低阶无穷小
B．高阶无穷小
C．同阶但非等价的无穷小
D．等价无穷小

4．设｛an｝，｛bn｝，｛cn｝均为非负数列，且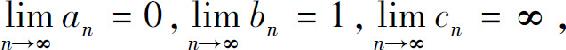则必有（　）．

A．an＜bn对任意n成立
B．bn＜cn对任意n成立
C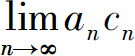．不存在
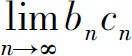D．不存在

5．当x→0＋时，与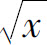等价的无穷小是（　）．

A．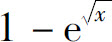
B．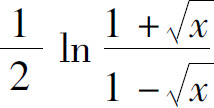
C．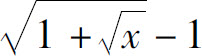
D．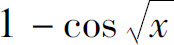

6．设f（x）在（－∞，＋∞）内单调有界，｛xn｝为数列，则下列命题正确的是（　）．

A．若｛xn｝收敛，则｛f（xn）｝收敛
B．若｛xn｝单调，则｛f（xn）｝收敛
C．若｛f（xn）｝收敛，则｛xn｝收敛
D．若｛f（xn）｝单调，则｛xn｝收敛

三、解答题

1．求下列极限：

（1）

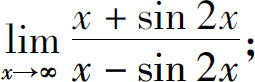
（2）

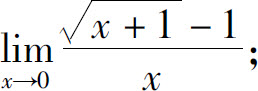
（3）

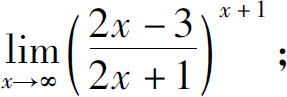
（4）

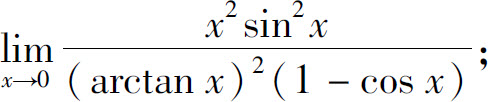
（5）

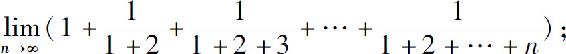
（6）

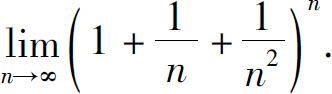
2．求下列极限：

（1）

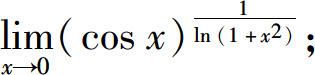
（2）

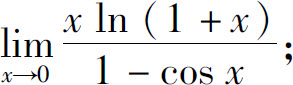
（3）

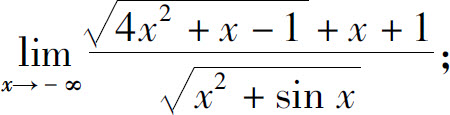
（4）

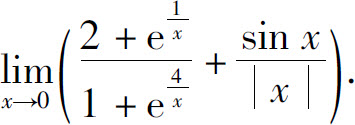
3．设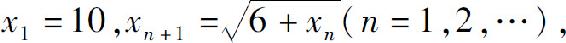试证明数列｛xn｝的极限存在，并求此极限．

4．证明方程x3－3x2－9x＋1＝0在（0，1）内至少有一实根．