2.4　隐函数和由参数方程所确定的函数的导数

2.4　隐函数和由参数方程所确定的函数的导数

2.4.1　隐函数的导数

前面所遇到的函数y都可由自变量x的解析式y＝f（x）来表示，这种函数称为显函数．如果变量x与y之间的函数关系由一个含x和y的方程F（x，y）＝0给出，那么称这种函数为由方程F（x，y）＝0所确定的隐函数．

例如，在方程x－y3＝1中，给x以任一确定值，相应地可确定y值，从而由方程确定函数y＝f（x）．这个函数就称为由x－y3＝1确定的隐函数．

把一个隐函数化成显函数，称为隐函数的显化．例如，从方程x－y3＝1中解出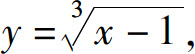就把隐函数化成了显函数．隐函数的显化有时是困难的，甚至是不可能的．能否直接由方程求出它所确定的隐函数的导数呢？

例1　求由方程y2＝x所确定的隐函数的导数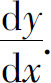

解　方程y2＝x确定了两个函数：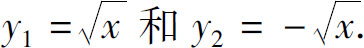

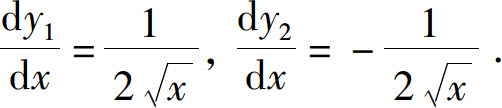
假如方程y2＝x确定隐函数不能显化，怎么求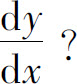

可对方程y2＝x两边求关于x的导数，把y＝f（x）当作x的可导函数来处理：

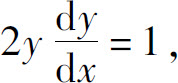
所以

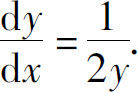
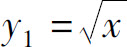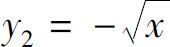上式给出了对显函数和所计算的导数：

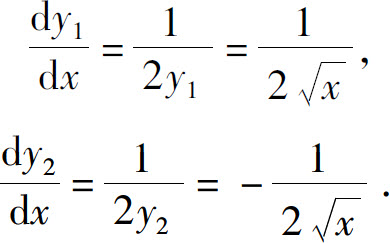
一般地，设方程F（x，y）＝0确定y为x的隐函数．对方程两边求关于x的导数，把y当作x的函数，可得一个包含的一次方程，解出即可．

例2　求由方程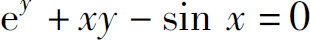所确定的隐函数的导数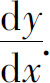

解　对方程两边关于x求导，注意y为x的函数，得

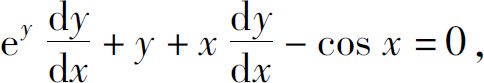
所以

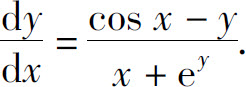
例3　求由方程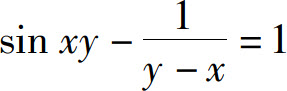所确定的隐函数在x＝0处的导数y′（0）．

解　方程两边对x求导，得

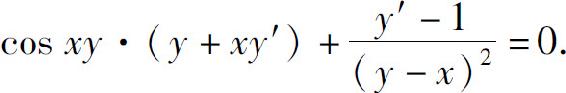
将x＝0代入原方程，得y（0）＝－1．再将它们代入上式，得

y′（0）＝2．

例4　求由方程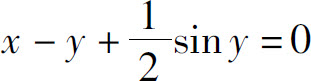所确定的隐函数的二阶导数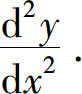

解　方程两边对x求导，得

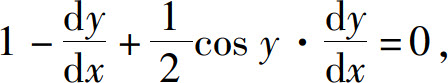
于是

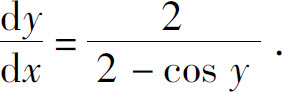
再对x求导，得

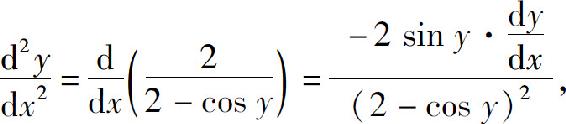
代入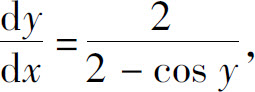得

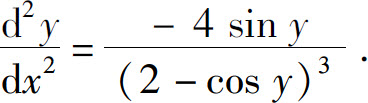
有时在求函数y＝f（x）的导数时，利用所谓对数求导法较为简便．这种方法是先在y＝f（x）的两边取对数，然后利用隐函数微分法求出y的导数．

例5　求函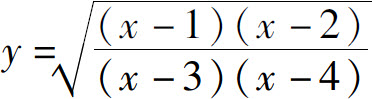数的导数．

解　取对数，得

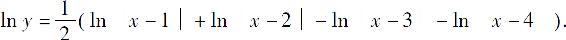
两边对x求导数，得

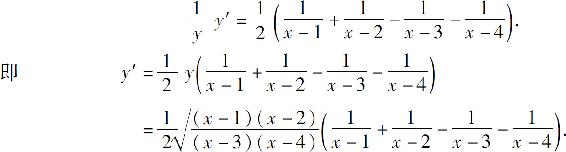
例6　求函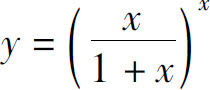数的导数．

解　这是一个幂指函数，为此取对数

ln y＝x（ln｜x｜－ln｜1＋x｜），

两边对x求导数，得

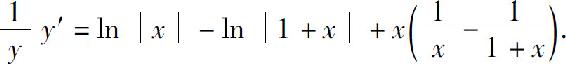
所以

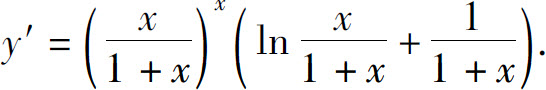
2.4.2　由参数方程所确定的函数的导数

如果参数方程

确定了y是x的函数，则称此函数为由参数方程（1）所确定的函数．

设函数x＝φ（t）有反函数t＝φ－1（x），那么由参数方程（1）所确定的函数可以看成是由函数y＝ψ（t），t＝φ－1（x）组成的复合函数

y＝ψ［φ－1（x）］．

现在来计算这个复合函数的导数．假设函数x＝φ（t），y＝ψ（t）都可导，而且φ′（t）≠0．于是根据复合函数的求导法则与反函数的求导法则，就有

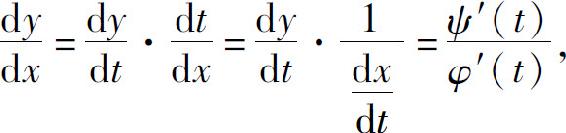
即

上式也可写成

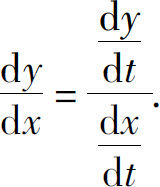
式（2）就是由参数方程（1）所确定的函数的求导公式．

作为x的函数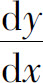，应表述为

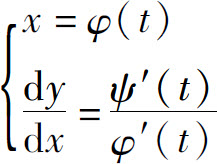
把上式中的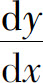看作式（1）中的y，由公式（2）有

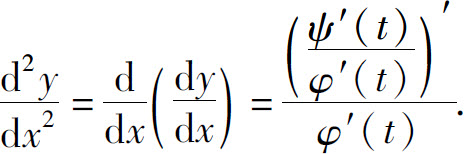
例7　已知椭圆的参数方程

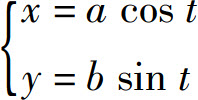
求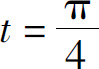相应的点处的切线方程.

解　当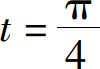时，椭圆上的相应点M的坐标为

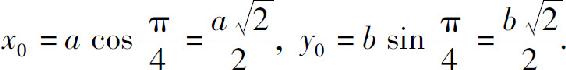
曲线在点M处的切线斜率为

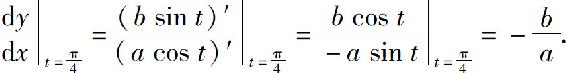
所以椭圆在点M处的切线方程为

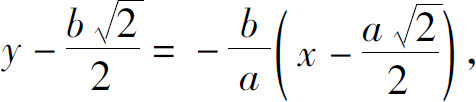
即

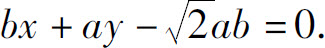
例8　求由参数方程

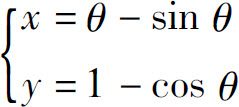
所确定的函数y＝f（x）的二阶导数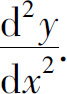

解

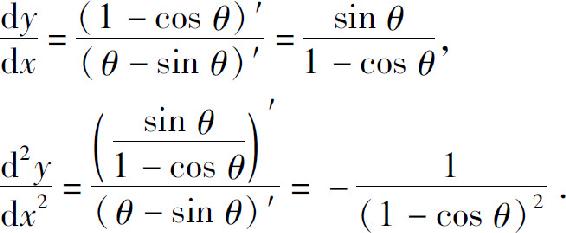
习题2.4

1．求由下列方程所确定的隐函数的导数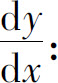

（1）

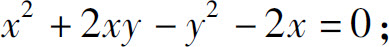
（2）

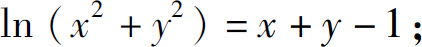
（3）

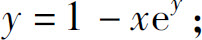
（4）

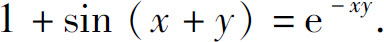
2．试用对数求导法求下列函数的导数：

（1）

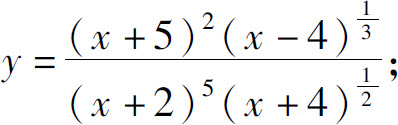
（2）

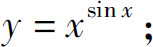
（3）

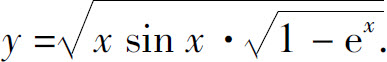
3．求由方程x2＋y2＝R2所确定的隐函数y（x）的二阶导数.

4．求由参数方程确定的函数的导数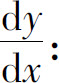

（1）

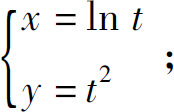
（2）

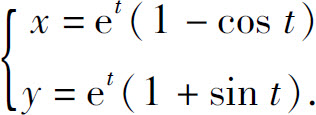
5．求曲线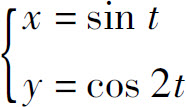在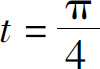相应点处的切线方程与法线方程.

6．证明曲线

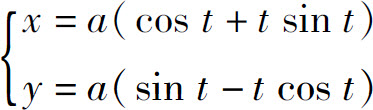
上任一点的法线与原点距离等于a.