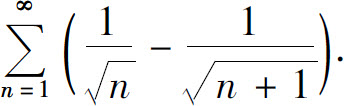8.1 数项级数的概念与性质
8.1 数项级数的概念与性质
8.1.1 数项级数的概念
设给定数列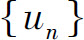
，则表达式
称为（常数项）无穷级数，简称（数项）级数，记为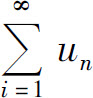
，即
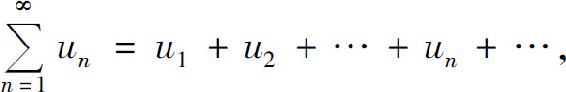
其中第n项un称为级数的一般项或通项．
例如，级数
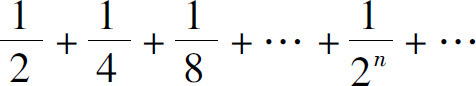
的通项为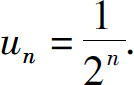
级数
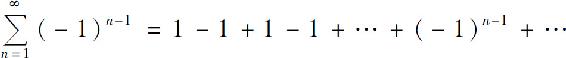
的通项为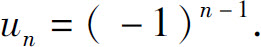
式（1）只是形式上的和式，因为逐项相加对无穷多项来说是无法实现的．怎么理解无穷多个数相加呢？我们从怎样界定无穷级数
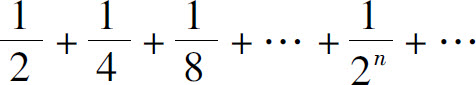
的意义开始．为此从第1项开始一次加一项，并考察这些“部分和”的变动情况：
部分和组成一个数列，其第n项
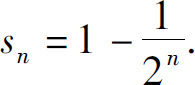
因为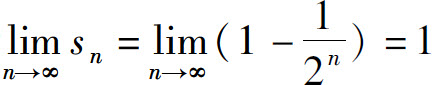
，我们称无穷级数
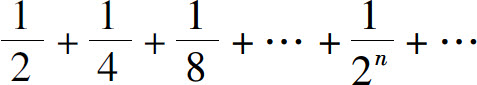的和为1．
定义 如果级数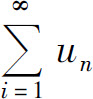
的部分和数列
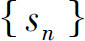收敛于s，即
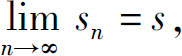
则称级数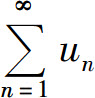
收敛，极限s称为级数的和，记为
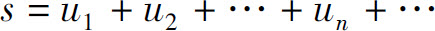
否则称级数发散．
由定义可知，讨论级数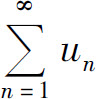
是否收敛的问题实质上就是考察部分和数列
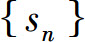是否收敛的问题．
例1 讨论首项为a（≠0），公比为q为几何级数（等比级数）
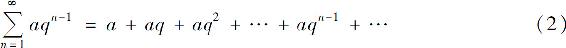
的收敛性．
解 当q≠1时，级数的部分和
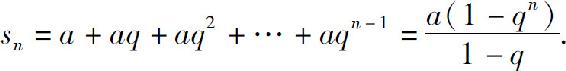
当｜q｜＜1时，由于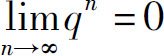
，从而几何级数（2）收敛，其和为
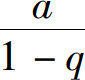；当|q|＞1时，由于
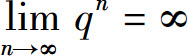，从而级数（2）发散；当q＝－1时，级数（2）为
a－a＋a－a＋…
故n为奇数时sn＝a，n为偶数时sn＝0，于是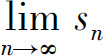
不存在，从而级数（2）发散．
当q＝1时，sn＝na→∞，从而级数（2）发散．
综上所述，如果公比的绝对值|q|＜1，则几何级数收敛，和为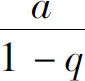
；如果|q|≥1，则几何级数发散．
特别地，记q＝x，当a＝1且|x|＜1时有
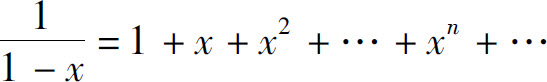
这是以后经常用到的结果．
例2 证明级数
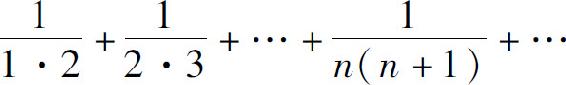
收敛，并求其和．
证 级数的部分和
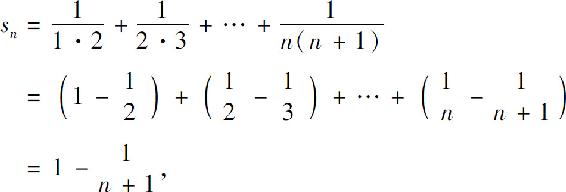
从而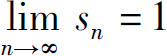
，所以级数收敛，其和为1．
例3 把循环小数2.717171…表示成两个整数之比．
解
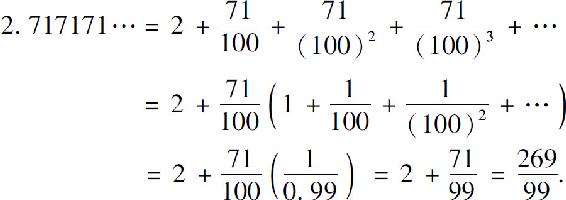
当无穷级数收敛时，其部分和sn是级数的和s的近似值，它们之间的差
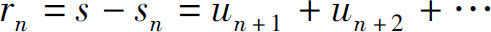
称为级数的余项．用sn近似s所产生的误差是这个余项的绝对值，即误差为|rn|．
由于
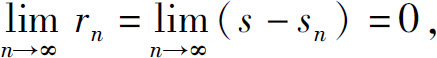
所以当n充分大时，这个误差可以任意小．
例4 几个发散级数
（1）级数
1－1＋1－1＋1－1＋…
把级数的项两两分组为
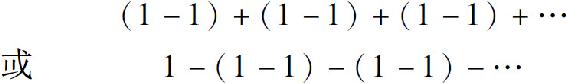
从而得到级数的和分别为0或1．但这种做法是错误的，因为这是一个无穷级数，而非有限个数相加，加法结合律不适用．事实上，如果它有和，则必须是部分和数列
1，0，1，0，1，…
的极限．因为这个数列没有极限，从而级数发散．
（2）级数
a＋a＋…＋a＋… （a为非零常数）
其部分和
sn＝na→∞（n→∞），
所以级数发散．
（3）级数
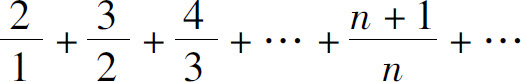
其部分和
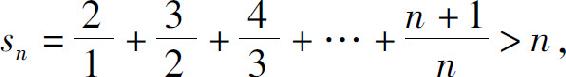
所以级数发散．
我们注意到，如果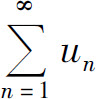
收敛，则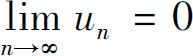
．事实上，设级数
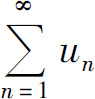的部分和为sn，如果
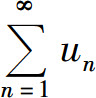收敛于s，即
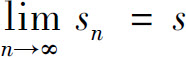，则
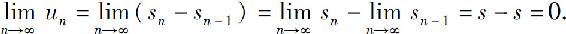
定理（级数收敛的必要条件） 如果级数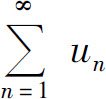
收敛，则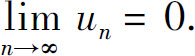
由定理可知，如果级数的通项不趋于零，则该级数一定发散，从而定理给出了判定级数发散的一个简便直接的方法．例如，例4中的3个级数，它们通项的极限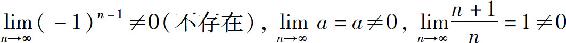
，所以级数发散．
值得注意的是，通项趋于零只是级数收敛的必要条件而不是充分条件．也就是说，通项趋于零的级数也可能发散．例如，调和级数
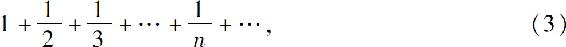
它的通项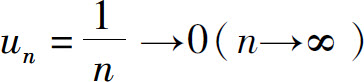
，但是它是发散的．用反证法证明如下：
假设级数（3）是收敛的，它的部分和为sn，且sn→s（n→∞）．显然，对级数（3）前2n项的部分和s2n，也有s2n→s（n→∞）．于是
s2n－sn→s－s＝0 （n→∞）．
另一方面
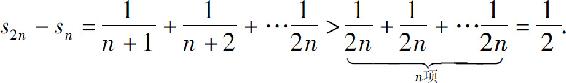
故n→∞时，s2n－sn不趋于零，矛盾，所以调和级数必定发散．
调和级数的部分和趋于无穷大，但趋于无穷大的速度极其缓慢．
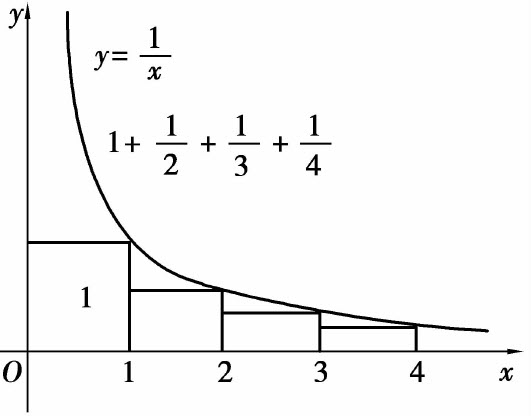
例5 为使调和级数的部分和大于20，大约需要多少项？
解 用sn表示调和级数的前n项部分和．比较图8.1与图8.2，可看出
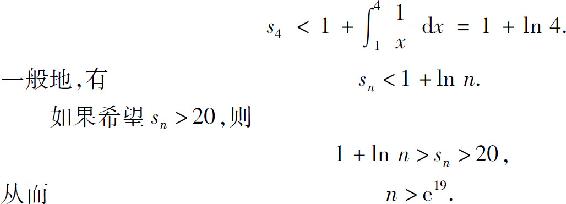
，所以至少要取调和级数的这么多项，才能使部分和超过20．
 |
 |
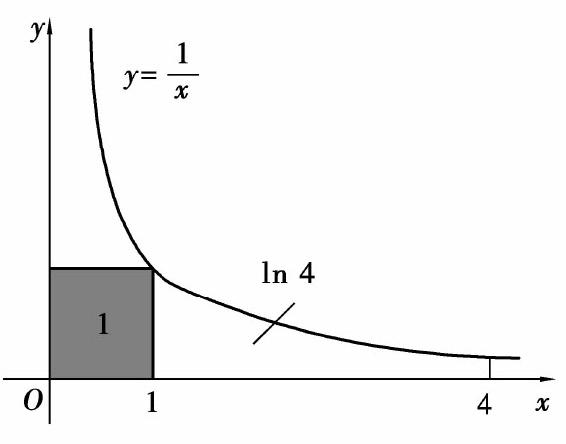| 图8.1 | 图8.2 |
8.1.2 收敛级数的性质
性质1 如果级数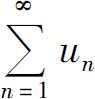
收敛于s，则级数
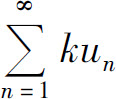（k为常数）也收敛，并且其和为ks．
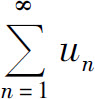证 设级数
与级数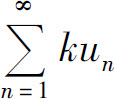
的部分和分别为sn和σn，则
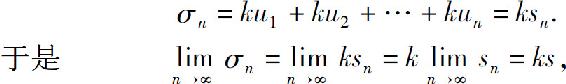
即级数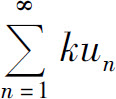
收敛，其和为ks．
性质2 如果级数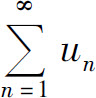
与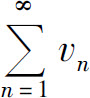
分别收敛于s与σ，则级数
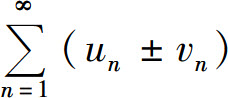也收敛，并且其和为s＋σ．
证 设级数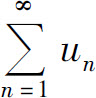
与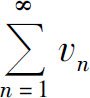
的部分和分别为sn和σn，则级数
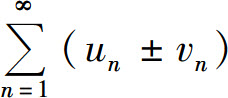的部分和
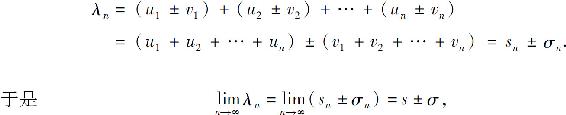
所以级数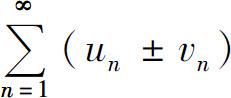
也收敛，并且其和为s±σ．
这个性质也可表述为：两个收敛级数可以逐项相加与逐项相减．
需要注意的是，两个发散的级数逐项相加减后得到的级数可能收敛也可能发散；而一个收敛的级数和一个发散的级数逐项相加减后得到的级数一定发散．
性质3 去掉级数的前有限项或在级数前面加上有限项不会改变级数的收敛性．
证 设将级数
u1＋u2＋…＋uk＋uk＋1＋…＋uk＋n＋…
的前k项去掉，则得级数
uk＋1＋uk＋2＋…＋uk＋n＋…．
于是新级数的部分和为
σn＝uk＋1＋uk＋2＋…＋uk＋n＝sk＋n－sk，
其中sk＋n是原级数的前k＋n项的和．因为sk是常数，所以当n→∞时，σn与sk＋n同时收敛或同时发散，因此去掉级数的前有限项不会改变级数的收敛性，但级数的和是会改变的．
类似可证明，在级数前面加上有限项不会改变级数的收敛性．
因为在级数中去掉、加上或改变有限项，都可以看成去掉级数的前有限项，然后在级数前面加上有限项的结果．因此有如下推论：
推论 级数中去掉、加上或改变有限项不会改变级数的收敛性．
例如级数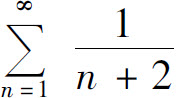
发散，因为它是调和级数
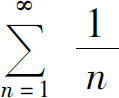去掉了前两项得到的级数．
例6 判断下列级数的收敛性：
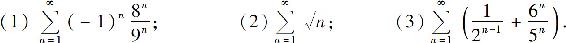
解 （1）级数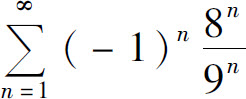
是以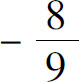
为公比的几何级数，且
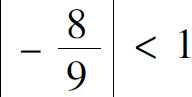，所以级数收敛．
（2）级数的通项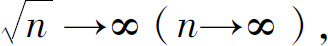
由级数收敛的必要条件知级数发散．
（3）由于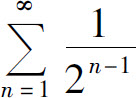级数
与级数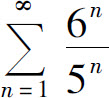
均为几何级数，公比分别为
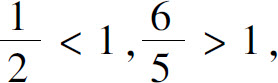故级数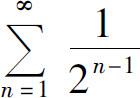
收敛，但级数
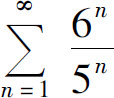发散．所以原级数发散．
习题8.1
1．写出下列级数的一般项：
（1）
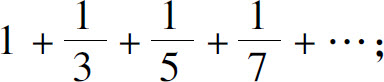
（2）
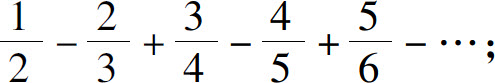
（3）
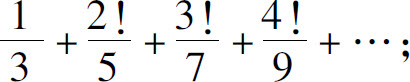
（4）
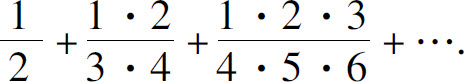
2．根据级数收敛的定义判定下列级数的收敛性：
（1）
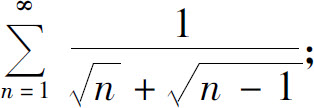
（2）
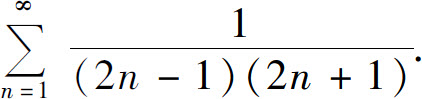
3．判定下列级数的收敛性：
（1）
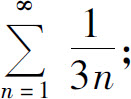
（2）
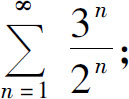
（3）
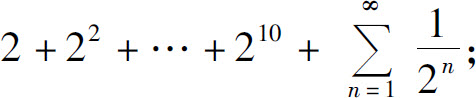
（4）
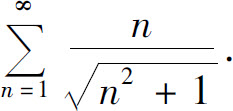
4．求下列级数的和：
（1）
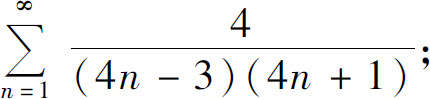
（2）
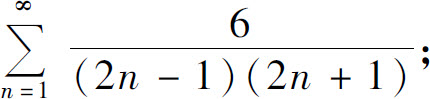
（3）