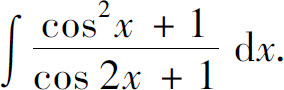4.1　不定积分的概念和性质

4.1　不定积分的概念和性质

4.1.1　不定积分的概念

1）原函数

定义1　设函数f（x）在区间I上有定义，如果存在函数F（x），使对于任意的x∈I，都有

F′（x）＝f（x），

则称F（x）为f（x）在I上的一个原函数．

例如，因为（sin x）′＝cos x，所以sin x就是cos x一个原函数．又由于（sin x＋1）′＝（sin x＋2）′＝cos x也成立，因此sin x＋1与sin x＋2也是cos x的原函数．一般地，sin x＋C（C为任意常数）都是cos x的原函数．

由此可见，若一个函数存在原函数，则它必有无穷多个原函数．进一步有如下定理：

定理1　如果F（x）是f（x）在区间I上的一个原函数，则F（x）＋C（C为任意常数）就表示函数f（x）在区间I上的所有原函数．

事实上，如果F（x）是f（x）的一个原函数，则［F（x）＋C］′＝f（x）（C为任意常数），所以F（x）＋C也是f（x）的原函数．

另一方面，如果F（x）和G（x）都是f（x）的原函数，即F′（x）＝G′（x）＝f（x），则由拉格朗日中值定理的推论可知，F（x）与G（x）仅差一个常数，即存在常数C使得G（x）＝F（x）＋C．

2）不定积分

定义2　称函数f（x）的带有任意常数的原函数为f（x）的不定积分，记为

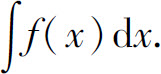
其中，符号∫称为积分号，x称为积分变量，f（x）称为被积函数，f（x）dx称为被积表达式．

由以上定义及前面的讨论可知，如果F（x）是f（x）的一个原函数，则F（x）＋C就是f（x）的不定积分，即

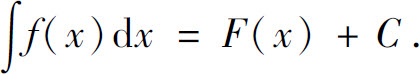
这里C称为积分常数．

例1　求不定积分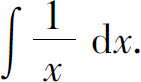

解　因为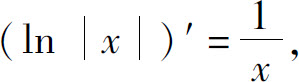所以有

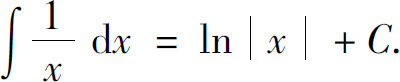
例2　设曲线通过点（1，3），且其上任一点处的切线斜率等于这点横坐标的两倍，求曲线方程．

解　设所求曲线方程为y＝f（x），由题设

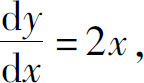
所以有

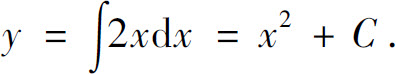
因曲线通过点（1，3），故3＝12＋C，得C＝2，从而所求的曲线方程为

y＝x2＋2．

函数f（x）的原函数的图形称为f（x）的积分曲线．例如，上例所求曲线即是函数2x通过点（1，3）的积分曲线．

例3　设某产品的边际成本为2x＋3，固定成本为2，求总成本函数C（x）．

解　因为（x2＋3x）′＝2x＋3，所以x2＋3x是2x＋3的一个原函数，从而

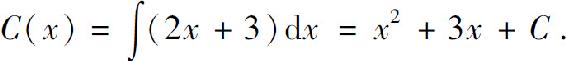
由C（0）＝2，可得C＝2，因此所求的总成本函数为

C（x）＝x2＋3x＋2．

在上面的例子中，所遇到的被积函数的原函数都存在．那么，一个函数具备什么条件，能保证它的原函数一定存在？我们不加证明地介绍如下结论：

定理2　如果f（x）在区间I上连续，则存在函数F（x），使对于任意的x∈I，都有

F′（x）＝f（x）．

简言之，连续函数一定有原函数．

4.1.2　不定积分性质

根据不定积分的定义和求导法则，可得到下列性质：

性质1　微分运算与积分运算的关系：

（1）

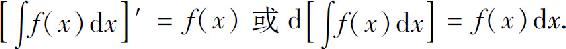
（2）

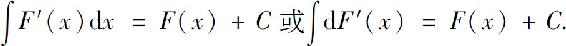
性质2　被积函数中不为零的常数因子可以移到积分号外，即

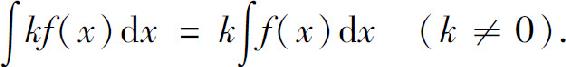
性质3　两个函数和的积分等于函数积分的和，即

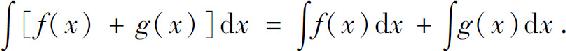
这一性质可以推广到有限多个函数的和的情形，即

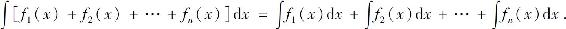
4.1.3　基本积分公式

由积分运算与微分运算的关系，根据基本导数公式可得如下的基本积分公式：

（1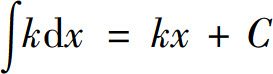）（k为常数）；

（2）

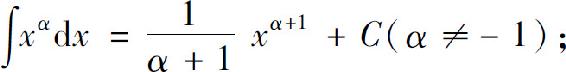
（3）

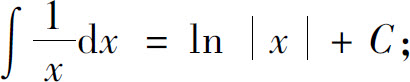
（4）

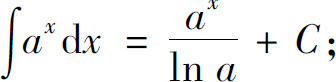
（5）

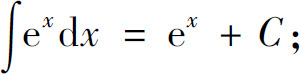
（6）

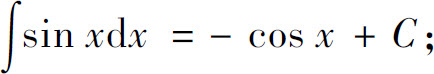
（7）

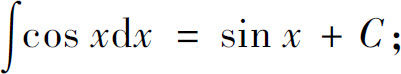
（8）

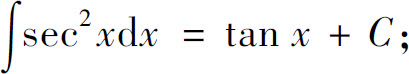
（9）

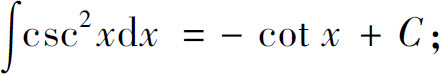
（10）

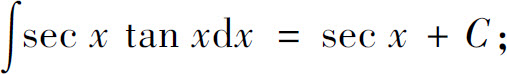
（11）

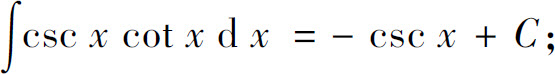
（12）

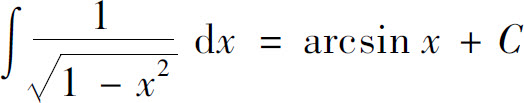
（13）

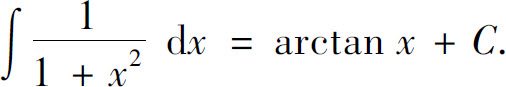
以上积分公式可通过对等式右端的函数求导进行验证．利用不定积分的性质以及上面的积分公式，可以计算一些函数的不定积分．

例4　求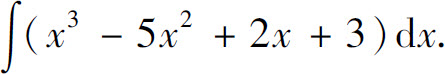

解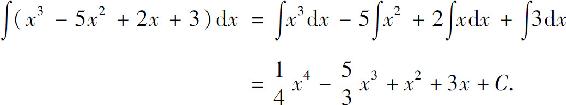　

例5　求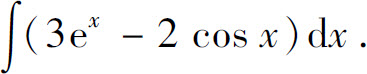

解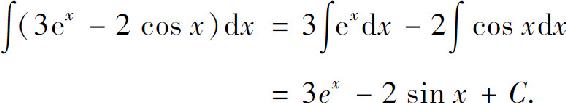　

例6　求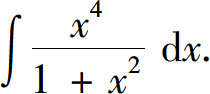

解

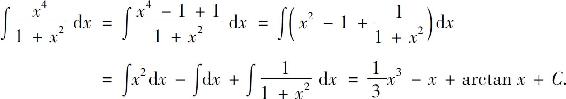
例7　求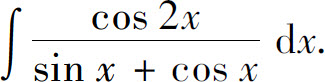

解

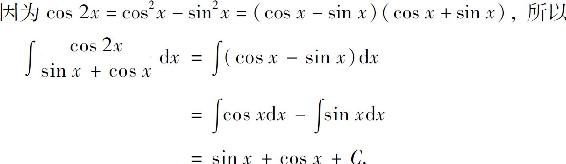
例8　求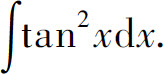

解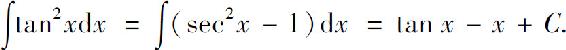　

例9　某种产品的产量q与生产时间t的关系为q＝q（t），则q关于t的导数q′（t）称为此种产品产量的变化率．若已知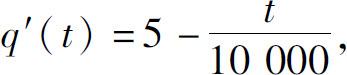试求此产品的产量与时间的关系．

解　因为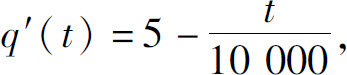所以

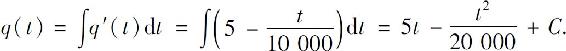
因为当生产时间为零时，产品产量也为零，所以q（0）＝C＝0．因此产量与生产时间的关系为

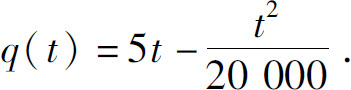
习题4.1

1．设已知函数F（x）是函数f（x）的一个原函数，试求函数2xf（x2）的一个原函数．

2．一曲线过点（e，2），且这曲线上任意一点的切线的斜率等于该点横坐标的倒数，求该曲线的方程．

3．求下列不定积分：

（1）

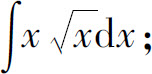
（2）

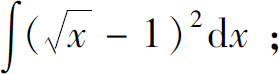
（3）

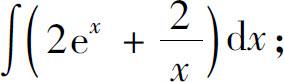
（4）

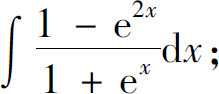
（5）

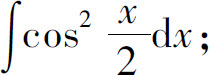
（6）

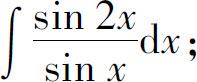
（7）

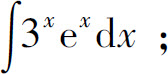
（8）

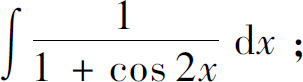
（9）

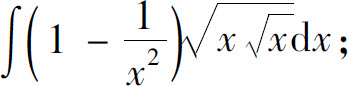
（10）

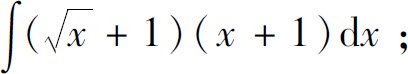
（11）

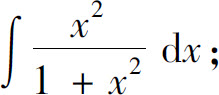
（12）

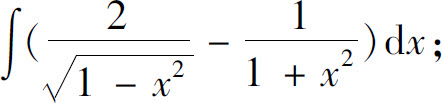
（13）

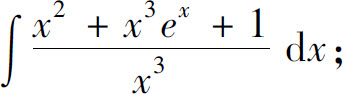
（14）

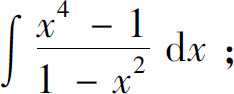
（15）

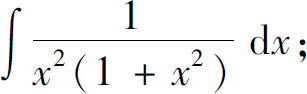
（16）

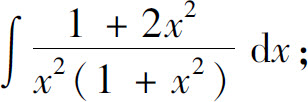
（17）

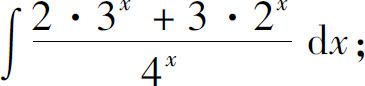
（18）

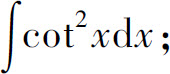
（19）

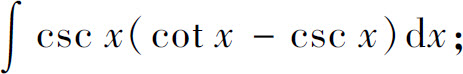
（20）

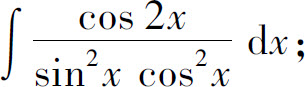
（21）