3.5 曲率
3.5 曲率
3.5.1 定义
曲线的“弯曲程度”是曲线的一种重要性态,在数学上用曲率来表示.
考察曲线的切线变化情况,就会发现,由于曲线的“弯曲性”,切线将随着切点的移动而旋转.切线转过的角度能够反映曲线的弯曲程度,另外,曲线的弯曲程度还与弧段的长度有关.
因此,引入描述曲线弯曲程度的曲率概念如下:
在曲线C上选定一点M0作为度量弧长的起点.对曲线上的任意点M,用s表示曲线弧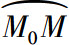 的长度(规定当点M在M0右侧时s>0).显然,弧长s是x的单调增加函数,如图3.15所示.
的长度(规定当点M在M0右侧时s>0).显然,弧长s是x的单调增加函数,如图3.15所示.
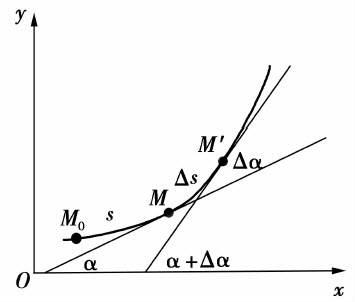
图3.15
设在点M处切线的倾角为α,曲线上另外一点M′对应于弧s+Δs,在点M′处切线的倾角为α+Δα,那么,弧段 的长度为|Δs|,当动点从M移动到M′时切线转过的角度为|Δα|.
的长度为|Δs|,当动点从M移动到M′时切线转过的角度为|Δα|.
用比值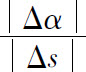 来表达弧段
来表达弧段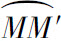 的平均弯曲程度,叫做弧段
的平均弯曲程度,叫做弧段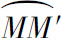 的平均曲率,并记作
的平均曲率,并记作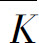 ,即
,即
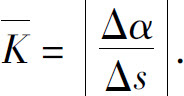
一般说来,曲线在各个点处弯曲程度不一样,|Δs|越小,用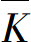 来描述曲线在点M处的弯曲程度越精确.当Δs→0(即M′→M)时,上述平均曲率的极限叫做曲线C在点M处的曲率,记作K,即
来描述曲线在点M处的弯曲程度越精确.当Δs→0(即M′→M)时,上述平均曲率的极限叫做曲线C在点M处的曲率,记作K,即

3.5.2 曲率的计算公式
1)求dα
设曲线方程为y=f(x),且f(x)具有二阶导数.因为tanα=y′,所以
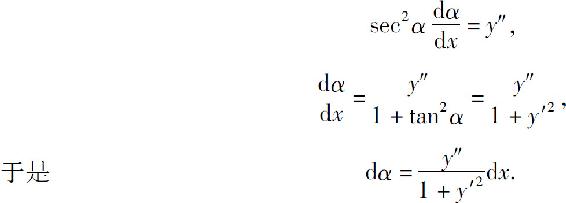
2)求ds.
考虑小弧段 ,当M′与M充分靠近时,可用弦
,当M′与M充分靠近时,可用弦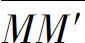 的长近似代替
的长近似代替 的弧长Δs,并有
的弧长Δs,并有
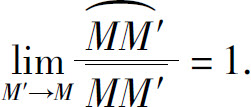
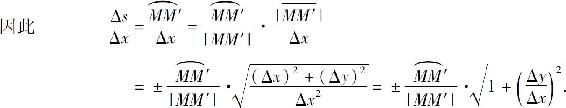
当M′→M,即Δx→0时取极限,就得到
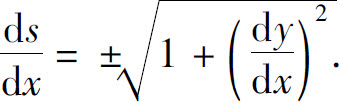
由于弧函数s(x)是x的单调增加函数,故
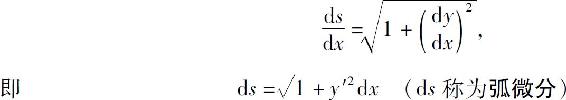
于是曲率K的计算公式为

例1 求直线的曲率.
解 设直线方程为y=mx+b(m为直线的斜率),则
y′=m,y″=0,
所以K=0,即直线的“弯曲程度”为0.
例2 求半径为a的圆的曲率.
解 设圆的方程为x2+y2=a2,用隐函数求导法,求得
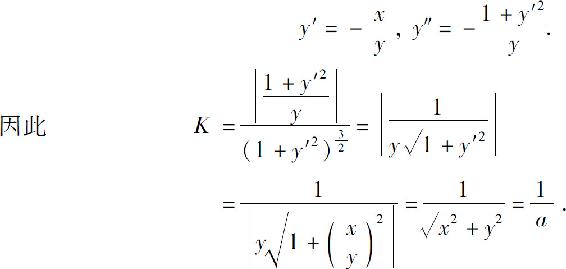
这说明圆周上任一点的曲率相等,其值等于圆半径的倒数.半径越小,曲率就越大;半径越大,曲率就越小.
例3 计算双曲线xy=1在点(1,1)处的曲率.
解 由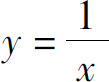 ,求导得
,求导得

把它们代入公式(2),便得曲线xy=1在点(1,1)处的曲率为
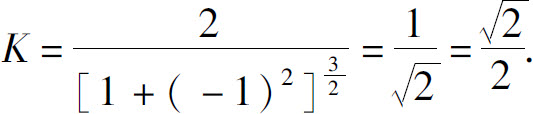
设曲线由参数方程
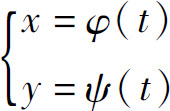
给出,则可利用由参数方程所确定的函数的导数公式求出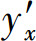 及
及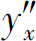 ,代入公式(2)便得
,代入公式(2)便得
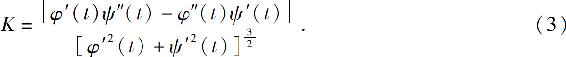
例4 求曲线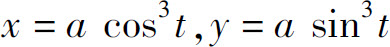 在t=t0相应点处的曲率.
在t=t0相应点处的曲率.
解
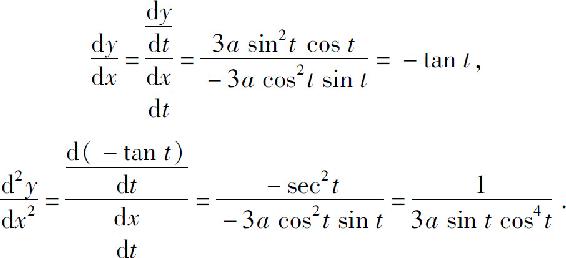
故曲线在t=t0相应点处的曲率为
设曲线y=f(x)在点M(x,y)处的曲率为K(K≠0).在点M(x,y)处的曲线的法线上,在凹的一侧取一点D,使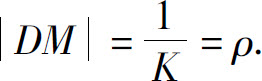 以D为圆心,ρ为半径作圆,如图3.16所示.这个圆叫做曲线在点M处的曲率圆,曲率圆的圆心D叫做曲线在点M处的曲率中心,曲率圆的半径ρ叫做曲线在点M处的曲率半径.
以D为圆心,ρ为半径作圆,如图3.16所示.这个圆叫做曲线在点M处的曲率圆,曲率圆的圆心D叫做曲线在点M处的曲率中心,曲率圆的半径ρ叫做曲线在点M处的曲率半径.
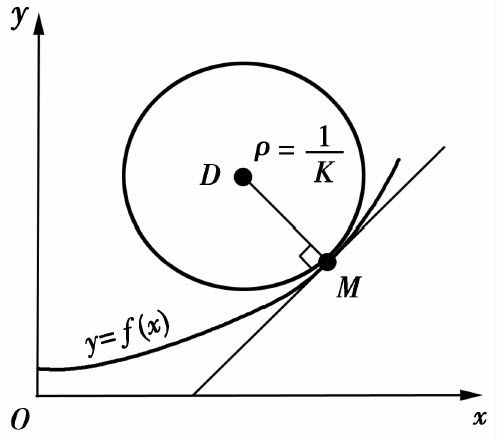
图3.16
按上述定义可知,曲率圆与曲线在点M有相同的切线和曲率,且在点M邻近有相同的凹凸方向.因此在实际问题中,常常用曲率圆在点M邻近的一段圆弧来近似代替曲线弧,以使问题简化.
习题3.5
1.求椭圆4x2+y2=4在点(0,2)处的曲率.
2.求曲线y=ln sec x在点(x,y)处的曲率及曲率半径.
3.求抛物线y=x2-4x+3在其顶点处的曲率及曲率半径.
4.对数曲线y=ln x上哪一点处的曲率半径最小?求出该点处的曲率半径.
5.导出极坐标方程形式下的曲线的曲率计算公式,并求曲线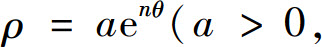 n>0)在点(ρ,θ)处的曲率.
n>0)在点(ρ,θ)处的曲率.
