习题7

习题7

一、填空题

1．微分方程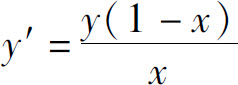的通解是_____．

2．求解微分方程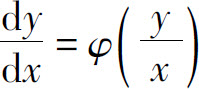时，可作变换_____．

3．微分方程xy′＋y＝0满足初始条件y（1）＝1的解是_____．

4．微分方程xy′＋2y＝x ln x满足初始条件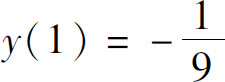的解为_____．

5．微分方程xy″＋3y′＝0的通解为_____．

6．微分方程yy″＋y′2＝0满足初始条件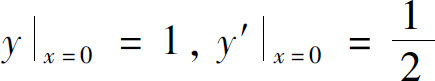的特解是_____．

7．二阶常系数线性微分方程y″＋py′＋qy＝0有两个相等的特征根r1＝r2，则方程的通解为_____．

8．设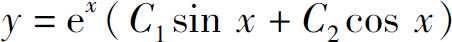（C1，C2为任意常数）为某二阶常系数线性齐次微分方程的通解，则该方程为_____．

9．设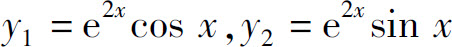是常系数微分方程y″＋by′＋cy＝0的两个解，则b＝_____，c＝_____．

10．二阶常系数非齐次线性微分方程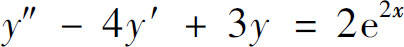的通解为y＝_____．

11．已知y＝1，y＝x，y＝x2是某二阶非齐次线性微分方程的三个解，则方程的通解为_____．

二、单项选择题

1．方程（y＋lnx）dx＋xdy＝0是（　）．

A．可分离变量方程
B．齐次方程
C．一阶非齐次线性方程
D．一阶齐次线性方程

2．已知y1＝cos 2x，y2＝3 sin 2x是方程y″＋4y＝0的解，则y＝C1y1＋C2y2（C1，C2为任意常数）是（　）．

A．是方程的通解
B．是方程的解，但不是通解
C．是方程的一个特解
D．不一定是方程的解

3．设C1，C2为任意常数，则微分方程y″－3y′＋2y＝0的通解为（　）．

A．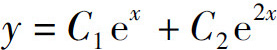
B．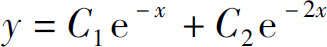
C．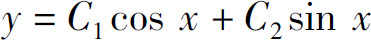
D．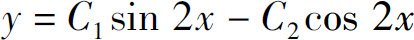

4．微分方程y″＋y＝x2＋1＋sin x的特解形式可设为（　　）．

A．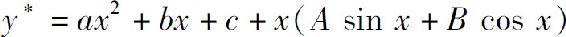
B．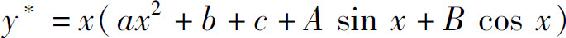
C．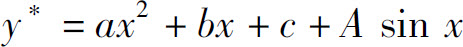
D．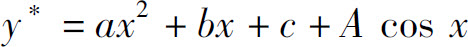

5．已知函数y＝y（x）在任意点处的增量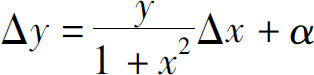，且当Δx→0时，α是Δx的高阶无穷小，y（0）＝π，则y（1）等于（　）．

A．2π
B．π
C．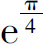
D．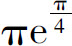

6．设方程y″＋qy＝0有当x→＋∞时趋于零的非零解，则（　）．

A．q＞0
B．q＝0
C．q＜0
D．q≤0

7．设y＝y（x）是二阶常系数线性微分方程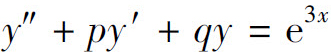满足初始条件y（0）＝0，y′（0）＝0的特解，则当x→0时，函数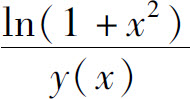的极限为（　）．

A．不存在
B．1
C．2
D．3

三、解答题

1．求以下列各式所表示的函数为通解的微分方程：

（1）（x＋C）2＋y2＝1（其中C为任意常数）；

（2）y＝C1ex＋C2e2x（其中C1，C2为任意常数）．

2．求下列微分方程的通解：

（1）

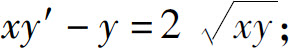
（2）

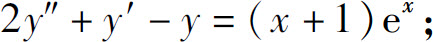
（3）

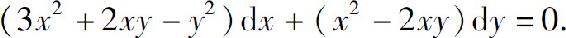
3．求下列微分方程满足所给初始条件的特解：

（1）

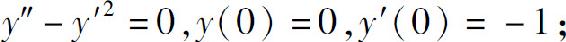
（2）

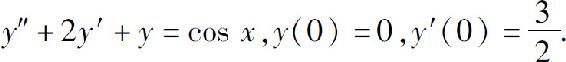
（3）

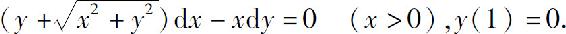
4．设可导函数φ（x）满足

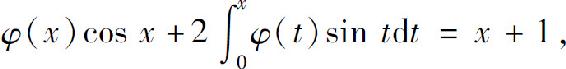
求φ（x）．

5．函数f（x）在［0，＋∞）上可导，f（0）＝1，且满足等式

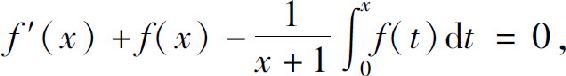
求导数f′（x）．

6．设函数y（x）（x≥0）二阶可导，且y′（x）＞0，y（0）＝1．过曲线y＝y（x）上任一点P（x，y）作该曲线的切线及x轴的垂线，上述两直线与x轴所围成的三角形的面积记为S1，区间［0，x］上以y＝y（x）为曲边梯形面积记为S2，并设2S1－S2恒为1，求此曲线y＝y（x）的方程．

7．某种飞机在机场降落时，为了减少滑行距离，在触地瞬间，飞机尾部张开减速伞，以增大阻力，使飞机迅速减速并停下．现有一质量为9000kg的飞机，着陆时的水平速度为700km/h．经测试，减速伞打开后，飞机所受的阻力与飞机的速度成正比（比例系数k＝6.0×106）．问从着陆点算起，飞机滑行的最大距离是多少？