5.4 广义积分
5.4 广义积分
定积分是在被积函数有界、积分区间有限的基础上定义的.但在一些实际问题中,我们常遇到积分区间为无穷区间,或者被积函数为无界函数的积分,这两类积分统称为广义积分.
5.4.1 无穷区间上的广义积分
定义1 设函数f(x)在区间[a,+∞)上连续,定义
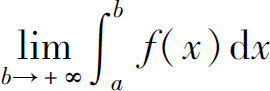
为函数f(x)在区间[a,+∞)上的广义积分,记作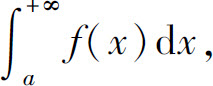 即
即
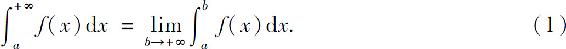
如果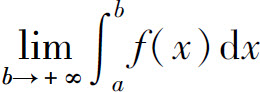 存在,则称广义积分
存在,则称广义积分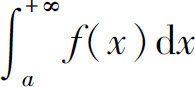 收敛,否则称广义积分
收敛,否则称广义积分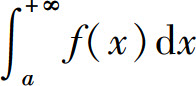 发散.
发散.
同样地,定义函数f(x)在区间(-∞,b]上的广义积分
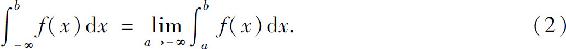
设函数f(x)在区间(-∞,+∞)上连续,定义f(x)在区间(-∞,+∞)上的广义积分
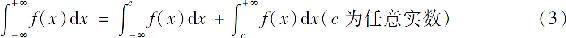
当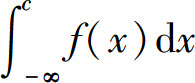 和
和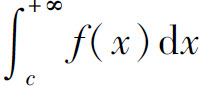 都收敛时,称广义积分
都收敛时,称广义积分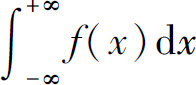 收敛,否则称广义积分
收敛,否则称广义积分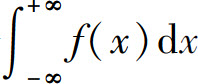 发散.
发散.
无穷区间上的广义积分又称为无穷积分.
例1 计算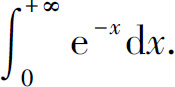
解 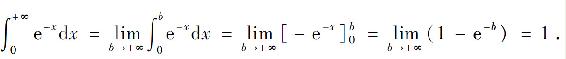
例2 计算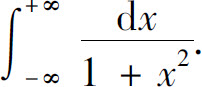
解 由式(3)得
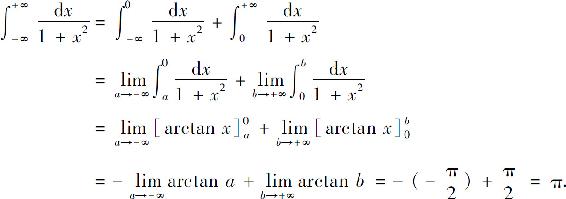
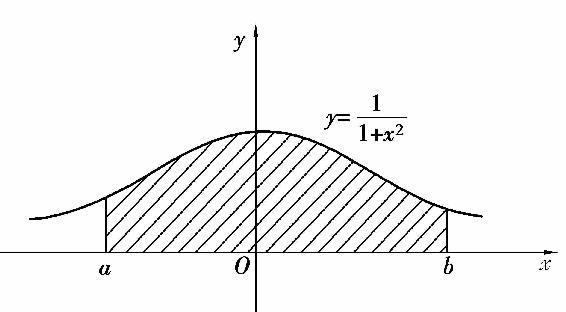
图5.5
这个广义积分的几何意义是:当a→-∞,b→+∞时,虽然图5.5中阴影部分向左、右无限延伸,但其面积却有极限值π.简单地说,它是位于曲线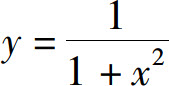 的下方、x轴上方的图形的面积.
的下方、x轴上方的图形的面积.
如果记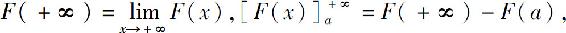 当F(+∞)存在时,
当F(+∞)存在时,
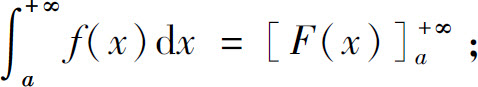
当F(+∞)不存在时,广义积分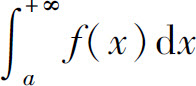 发散.其他情形类似.
发散.其他情形类似.
例3 证明:广义积分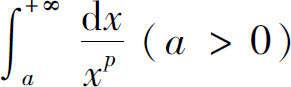 当p>1时收敛,当p≤1时发散.
当p>1时收敛,当p≤1时发散.
证 当p≠1时
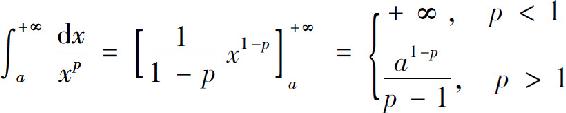
当p=1时
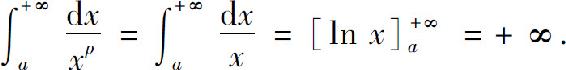
因此,当p>1时广义积分收敛,其值为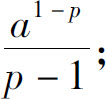 当p≤1时,广义积分发散.
当p≤1时,广义积分发散.
5.4.2 无界函数的广义积分
定义2 设函数f(x)在区间(a,b]上连续,且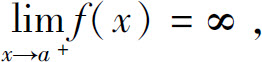 定义
定义
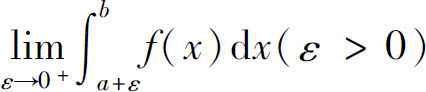
为无界函数f(x)在区间(a,b]上的广义积分,仍记作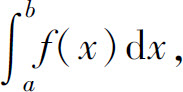 即
即
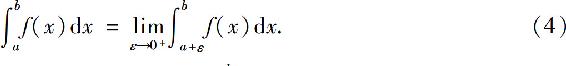
如果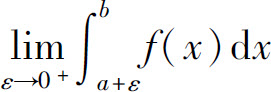 存在,则称广义积分
存在,则称广义积分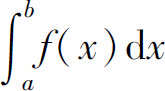 收敛.否则称广义积分
收敛.否则称广义积分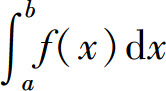 发散.
发散.
同样地,设函数f(x)在区间[a,b)上连续,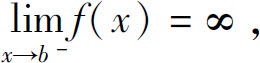 则定义广义积分
则定义广义积分
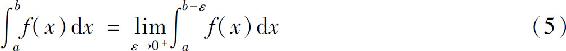
设函数f(x)在区间[a,b]上除点c(a<c<b)外连续,且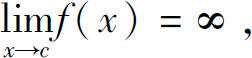 则定义广义积分
则定义广义积分
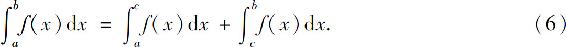
当两个广义积分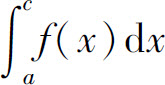 和
和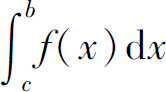 都收敛,则称广义积分
都收敛,则称广义积分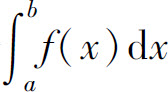 收敛,否则称广义积分
收敛,否则称广义积分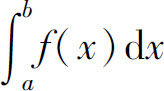 发散.
发散.
上述定义的广义积分统称为无界函数的广义积分.
如果函数在一点附近无界,则称这点为函数f(x)的瑕点(或奇点),因此无界函数的广义积分又称为瑕积分.
例4 计算广义积分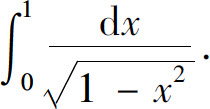
解 因为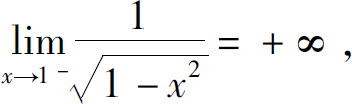 所以点1是瑕点.于是
所以点1是瑕点.于是
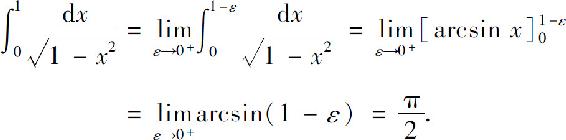
例5 证明广义积分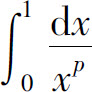 当0<p<1时收敛,当p≥1时发散.
当0<p<1时收敛,当p≥1时发散.
证 当p>0且p≠1时,有
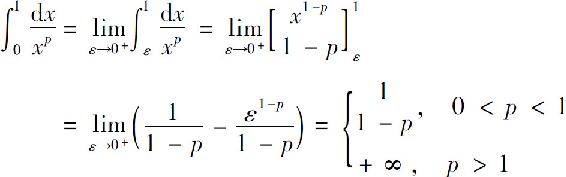
当p=1时,有
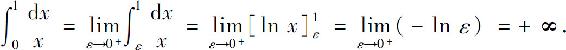
所以,当0<p<1时,广义积分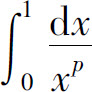 收敛;当p≥1时,
收敛;当p≥1时,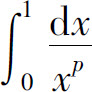 发散.
发散.
最后要说明的是,与定积分类似,广义积分也有换元法.
例6 计算广义积分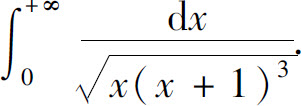
解 积分下限x=0为瑕点,令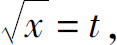 ,则x=t2,且当x→0+时,t→0;当x→+∞时,t→+∞.于是
,则x=t2,且当x→0+时,t→0;当x→+∞时,t→+∞.于是
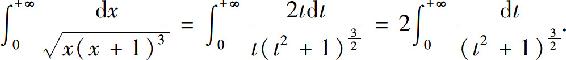
再令t=tan u,则u=arctan t,且当t=0时,u=0;当t→+∞时,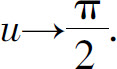 于是
于是
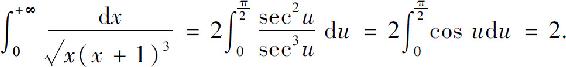
习题5.4
1.判别下列广义积分的收敛性;如果收敛,计算广义积分的值:
(1)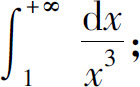
(2)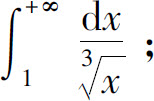
(3)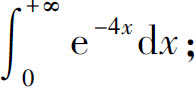
(4)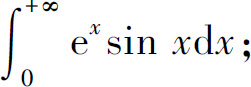
(5)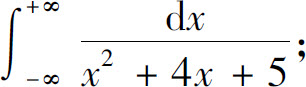
(6)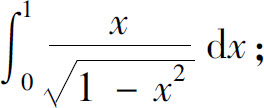
(7)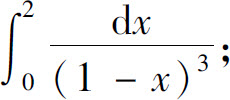
(8)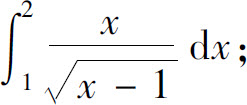
(9)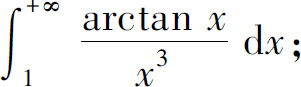
(10)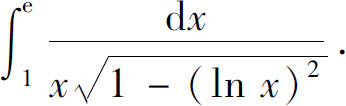
2.当k为何值时,广义积分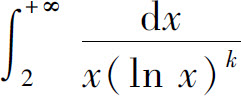 收敛?当k为何值时,这广义积分发散?当k为何值时,这广义积分取得最小值?
收敛?当k为何值时,这广义积分发散?当k为何值时,这广义积分取得最小值?
