习题3
习题3
一、填空题
1.函数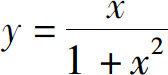 的单调增加区间为_____.
的单调增加区间为_____.
2.设函数g(x)有一阶连续导数,且g(0)=g′(0)=1,则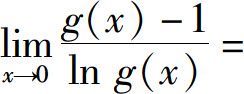 _____.
_____.
3.若点(1,0)是曲线y=ax3+bx2+2的拐点,则a=_____,b=_____.
4.曲线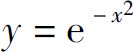 的凸区间为_____.
的凸区间为_____.
5.设f(0)=1,f′(0)=-1,则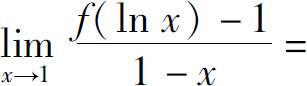 _____.
_____.
6.曲线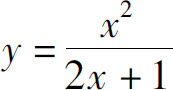 的斜渐近线方程为_____.
的斜渐近线方程为_____.
二、单项选择题
1.当x→0时,若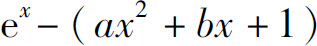 是比x2高阶的无穷小,则a,b值为( ).
是比x2高阶的无穷小,则a,b值为( ).
A.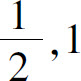
B.1,1
C.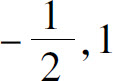
D.-1,1
2.若在区间(a,b)内有f′(x)<0,f″(x)<0,则曲线y=f(x)在此区间内是( ).
A.下降且是凸的
B.下降且是凹的
C.上升且是凸的
D.上升且是凹的
3.函数y=arcsin x-x的单调增加区间为( ).
A.(-∞,+∞)
B.(0,1)
C.(-1,1)
D.(-1,0)
4.以下命题正确的有( ).
A.若对任意x∈(a,b),都有f′(x)=0,则f(x)在(a,b)内恒为常数
B.若x0为f(x)的极值点,则必有f′(x0)=0
C.函数f(x)在(a,b)内的极大值必定大于极小值
D.若f′(x0)=0,则x0为f(x)的极值点
5.设f(x)与g(x)在x=x0处均有极大值,则函数F(x)=f(x)g(x)在x=x0处( ).
A.必有极大值
B.必有极小值
C.没有极值
D.是否有极值不能确定
6.函数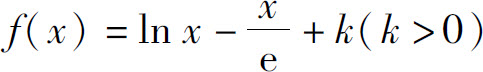 在(0,+∞)内的零点个数为( ).
在(0,+∞)内的零点个数为( ).
A.3
B.2
C.1
D.0
7.设在[0,1]上f″(x)>0,则f′(0),f′(1),f(1)-f(0)或f(0)-f(1)的大小顺序是( ).
A.f′(1)>f′(0)>f(1)-f(0)
B.f′(1)>f(1)-f(0)>f′(0)
C.f(1)-f(0)>f′(1)>f′(0)
D.f′(1)>f(0)-f(1)>f′(0)
8.设函数y=f(x)具有二阶导数,且f′(x)>0,f″(x)>0,Δx为自变量x在点x0处的增量,Δy与dy分别为f(x)在点x0处对应的增量与微分,若Δx>0,则( ).
A.0<dy<Δy
B.0<Δy<dy
C.Δy<dy<0
D.dy<Δy<0
9.设f(x)有二阶连续导数,且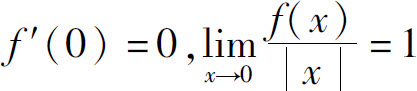 ,则( ).
,则( ).
A.f(0)是f(x)的极大值
B.f(0)是f(x)的极小值
C.(0,f(0))是曲线y=f(x)的拐点
D.f(0)不是f(x)的极值点,(0,f(0))也不是曲线y=f(x)的拐点
三、解答题
1.求下列极限:
(1)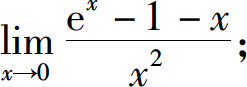
(2)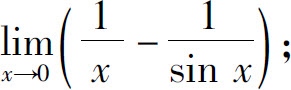
(3)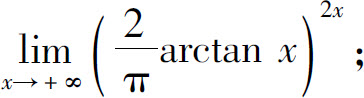
(4)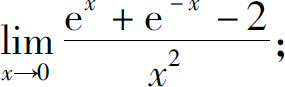
(5)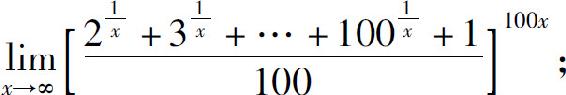
(6)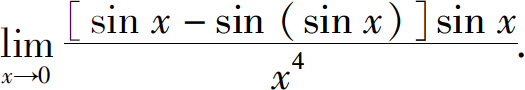
2.证明下列不等式:
(1)当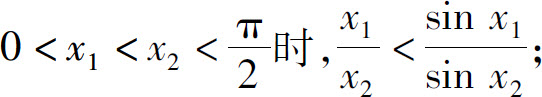
(2)|sin a-sin b|≤|a-b|;
(3)当x>0时,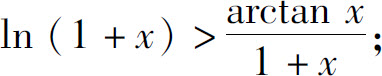
(4)设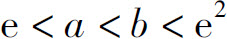 ,则
,则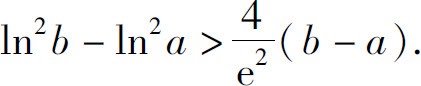
3.证明方程x5+x-1=0有且仅有一个正根.
4.如图3.17所示,三角形的底边长为a,高为h,求其最大内接矩形的面积.
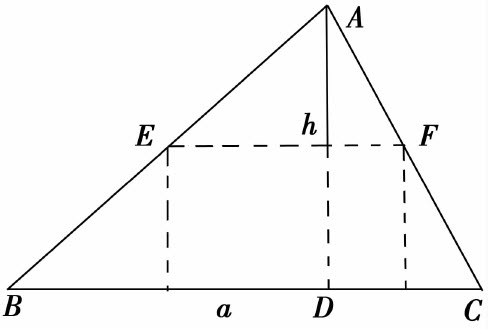
图3.17
5.讨论方程的根:
(1)x3-5x-2=0,在(0,+∞)内;
(2)a0+a1x+…+anxn=0,在(0,1)内,其中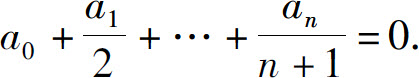
6.设f(x)在[0,a]上连续,在(0,a)内可导,且f(a)=0,证明存在一点ξ∈(0,a),使得
f(ξ)+ξf′(ξ)=0.
7.设0<a<b,函数f(x)在[a,b]上连续,在(a,b)内可导,证明存在一点ξ∈(a,b),使得
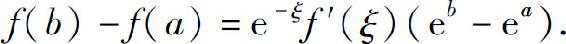
8.已知函数f(x)在[0,1]上连续,在(0,1)内可导,且f(0)=0,f(1)=1.证明:
(1)存在ξ∈(0,1),使得f(ξ)=1-ξ;
(2)存在两个不同的点η,ζ∈(0,1),使得f′(η)f′(ζ)=1.
9.曲线弧y=sin x(0<x<π)上哪一点处的曲率半径最小?求出该点处的曲率半径.
