习题6

习题6

一、填空题

1．函数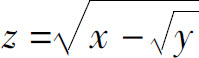的定义域是_____．

2．

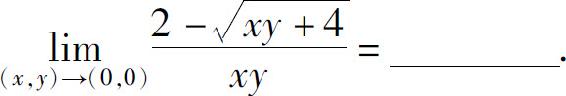
3．曲线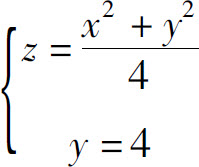在点（2，4，5）处的切线对于x轴的倾角是_____．

4．改变二次积分的积分次序：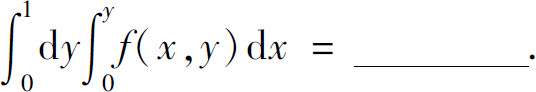

5．设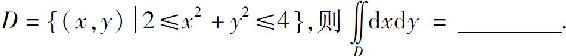

6．设f（u，v）为二元可微函数，z＝f（xy，yx），则

二、单项选择题

1．下面集合中（　）是闭集．

A．｛（x，y）|x≠0，y≠0｝
B．｛（x，y）|1＜x2＋y2≤4｝
C．｛（x，y）|y＞x2｝
D．｛（x，y）|x2＋（y－1）2≥1｝

2．设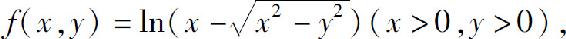则f（x＋y，x－y）＝（　）．

A．2 ln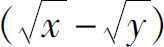
B．ln（x－y）
C．2（ln x－ln y）
D．2 ln（x－y）

3．函数f（x，y）在点（x0，y0）偏导数存在是f（x，y）在该点连续的（　）．

A．充分而不必要条件
B．必要而不充分条件
C．充分必要条件
D．既不是充分也不是必要条件

4．设函数f（x，y）在点（x0，y0）处可微，且fx（x0，y0）＝0，fy（x0，y0）＝0，则函数f（x，y）在点（x0，y0）处（　）．

A．有极值，可能是极大，也可能是极小
B．可能有极值，也可能无极值
C．有极大值
D．有极小值

5．设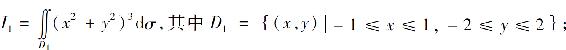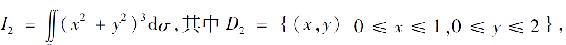则（　）．

A．I1＝I2
B．I1＝2I2
C．I1＝3I2
D．I1＝4I2

6．设f（x）为连续函数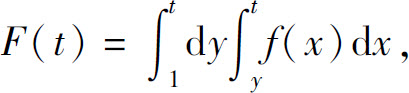，则F′（2）＝（　）．

A．2f（2）
B．f（2）
C．－f（2）
D．0

三、解答题

1．设u＝xy，而x＝φ（t），y＝ψ（t）都是可微函数，求．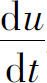

2．求下列函数的全微分：

（1）

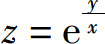
（2）

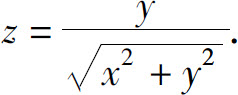
3．设．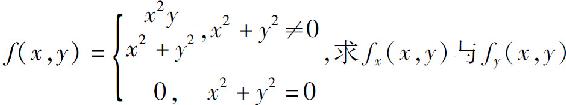

4．一个仓库的下半部是圆柱形，顶部是圆锥形，半径均为6m，总表面积为200m2（不包括底部）．问圆柱、圆锥的高各为多少时，仓库的容积最大？

5．求函数f（x，y）＝2x2＋3y2－4x＋2在闭区域D＝｛x，y|x2＋y2≤16｝上的最大值和最小值．

6．设z＝xy＋xF（u），而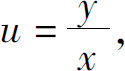F（u）为可导函数，证明：

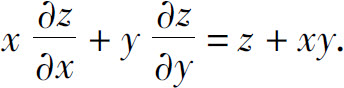
7．交换下列二次积分的次序：

（1）；

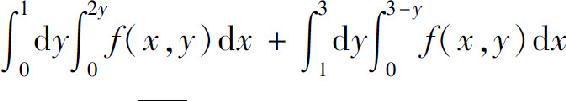（2）

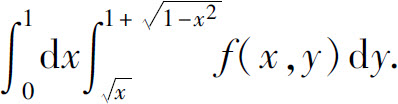
8．设函数f（x）在［0，1］上连续且．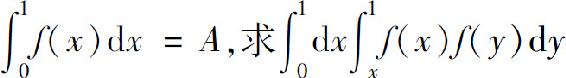

9．计算二重积分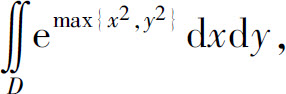，其中D＝｛（x，y）｜0≤x≤1，0≤y≤1｝．

10．设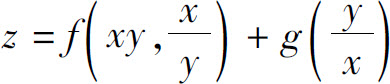，其中f具有二阶连续偏导数，g具有二阶连续导数，求．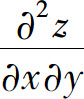