5.5 定积分的应用
5.5 定积分的应用
5.5.1 定积分的元素法
能够用定积分来计算的量Q,如曲边梯形的面积和变速直线运动的路程等,都有两个共同的特性:
(1)Q连续分布在某个区间[a,b]上;
(2)Q对区间[a,b]具有可加性:如果把区间[a,b]分成若干个部分区间,则Q相应地分成若干个部分量,且Q等于所有部分量之和.
如果用定积分的定义来推导Q的积分表达式,则要经过分割、近似、求和、取极限四个步骤,过于复杂.因此引入定积分的元素法.
要想得到Q的积分表达式,关键要得到积分中的被积表达式.假设Q已经表达为定积分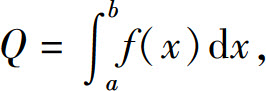 令
令
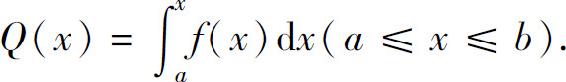
当f(x)在[a,b]上连续时,则dQ(x)=f(x)dx,即Q的积分式中的被积表达式是Q(x)的微分,此时dQ(x)=f(x)dx称为Q的(积分)元素.因此,求得Q的元素,再求其在[a,b]上的积分便得到所求量Q,这一方法称为定积分的元素法.
结合微分的性质,用元素法求量Q的步骤如下:
(1)在[a,b]中任取一个小区间[x,x+dx],将所求量Q在这小区间上相应的部分量ΔQ近似地表示为f(x)dx(通常采取以直代曲,以匀代变的方法);
(2)检验f(x)dx是否满足:f(x)在[a,b]上连续,并且
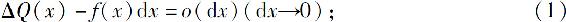
(3)当式(1)成立时,有dQ(x)=f(x)dx,积分就得
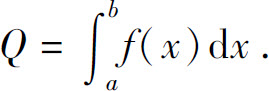
5.5.2 定积分在几何学上的应用
1)平面图形的面积
根据定积分的几何意义,由连续曲线y=f(x)(f(x)≥0),直线x=a,x=b及x轴所围成的曲边梯形的面积
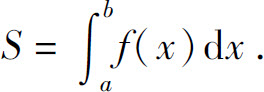
现考虑由连续曲线y=φ1(x),y=φ2(x)(φ1(x)≤φ2(x)),直线x=a,x=b(a<b)所围成的平面图形的面积S,如图5.6所示.
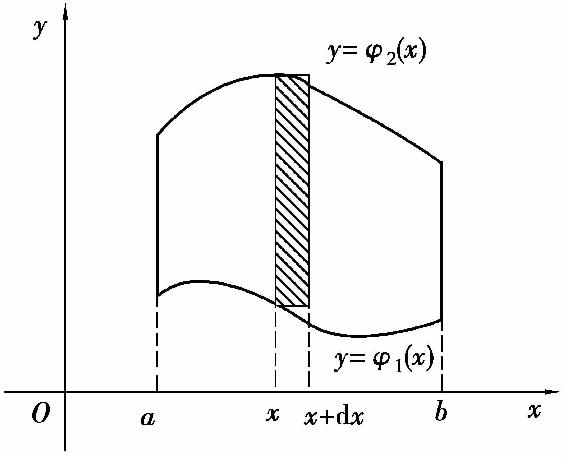
图5.6
在[a,b]中任取一个小区间[x,x+dx],面积S在这小区间上相应的部分量ΔS可近似看作长为φ2(x)-φ1(x)、宽为dx的矩形的面积,即
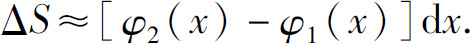
因为φ2(x)-φ1(x)连续,故在[x,x+dx]上有最大值M和最小值m,所以
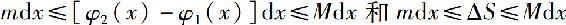
从而
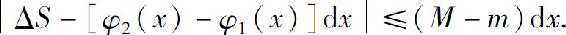
再由φ2(x)-φ1(x)连续知,dx→0时,M-m→0,所以
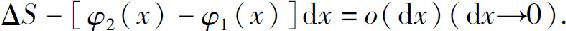
因此面积元素
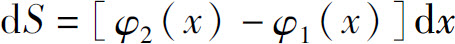
积分就得
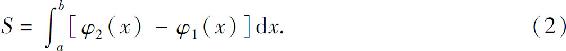
同理可得,由连续曲线x=ψ1(y),x=ψ2(y)(ψ1(y)≤ψ2(y))及直线y=c,y=d所围成的平面图形(图5.7)的面积为
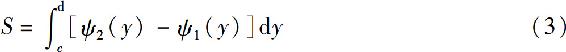
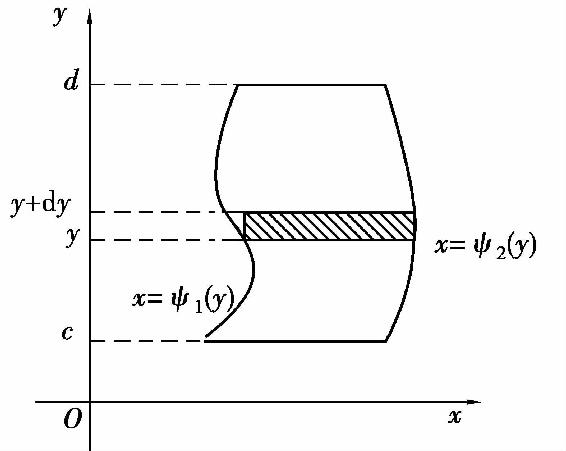
图5.7
例1 求由两条抛物线y=-x2+1与y=x2-x所围成的平面图形的面积.
解 解方程组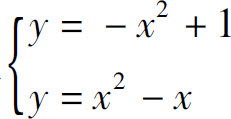 得交点为
得交点为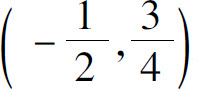 及(1,0).所围区域(图5.8)为
及(1,0).所围区域(图5.8)为
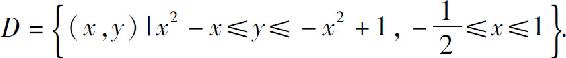
故所求面积
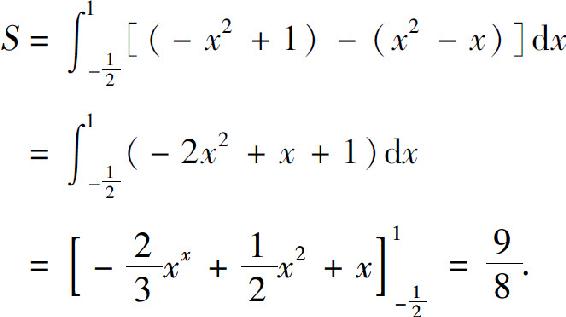
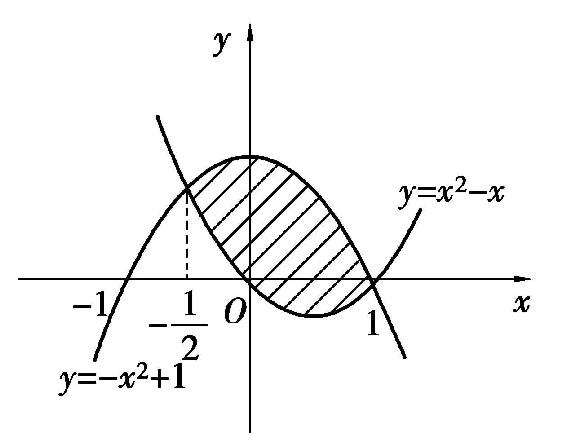
图5.8
例2 求抛物线y2=2x与直线y=x-4所围成的平面图形的面积.
解 解方程组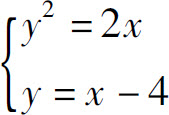 得交点为(2,-2)及(8,4).所围区域(图5.9)为
得交点为(2,-2)及(8,4).所围区域(图5.9)为
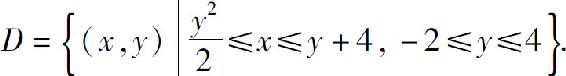
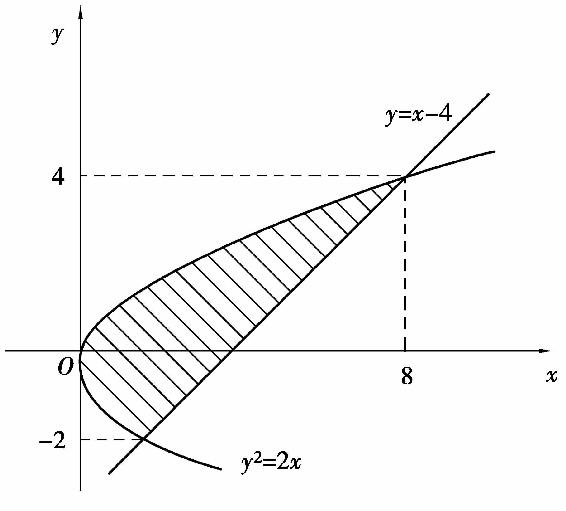
图5.9
故所求面积 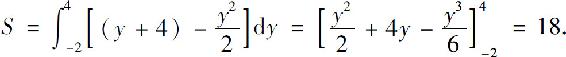
若利用公式(2)计算,则需要把图形分成两部分
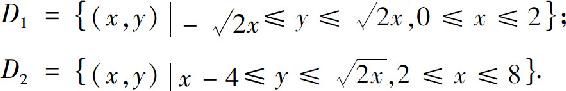
故
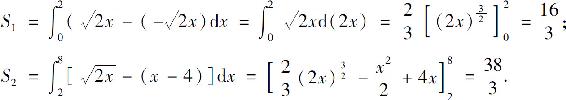
所求面积
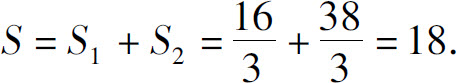
某些平面图形,利用极坐标计算它们的面积较为简便.
设平面图形由曲线r=r(θ)及射线θ=α,θ=β围成(简称曲边扇形),如图5.10所示.这里r(θ)在[α,β]上连续且非负.求平面图形的面积.
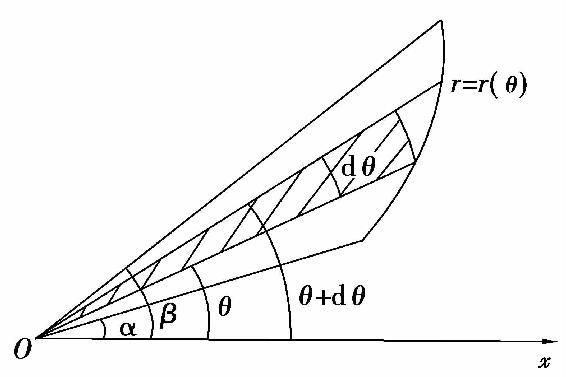
图5.10
在区间[α,β]上任取一小区间[θ,θ+dθ],在此小区间上,小曲边扇形的面积ΔS可以用半径为r=r(θ)、中心角为dθ的扇形的面积来近似,即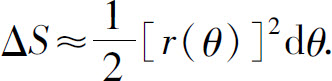 类似直角坐标的情形,可证
类似直角坐标的情形,可证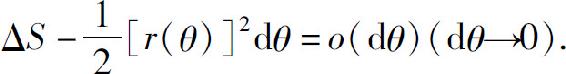 从而对曲边扇形的面积元素
从而对曲边扇形的面积元素
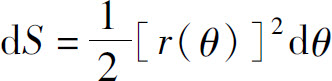
积分,便得所求曲边扇形的面积

例3 计算阿基米德螺线
r=aθ(a>0)
上相应于θ从0变到2π的一段弧与极轴所围成的图形(图5.11)的面积.
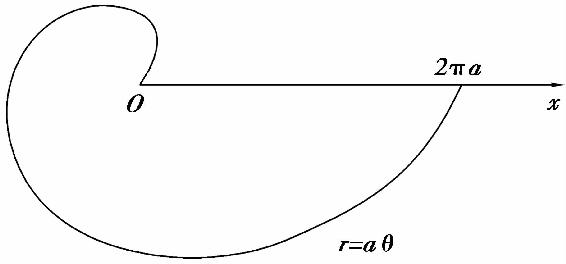
图5.11
解 由公式(4)得所求面积
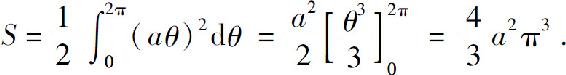
例4 求心形线
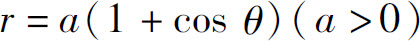
围成的图形的面积.
解 此曲线对称于极轴(x轴),位于x轴上方的面积是θ从0到π时曲线弧与x轴所围成,如图5.12所示.于是所求面积
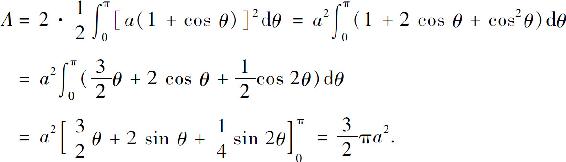
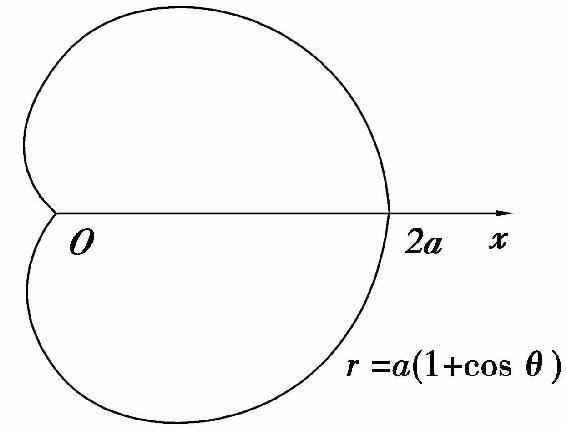
图5.12
2)已知平行截面面积的立体的体积
如果已知一个立体中垂直于一定轴的各个截面的面积,那么这个立体的体积也可以用定积分来计算.
如图5.13所示,取定轴为x轴,并设该立体在过点x=a,x=b且垂直于x轴的两个平面之间.以A(x)表示过点x且垂直于x轴的截面的面积.假定A(x)为x的已知的连续函数.我们来计算此立体的体积.
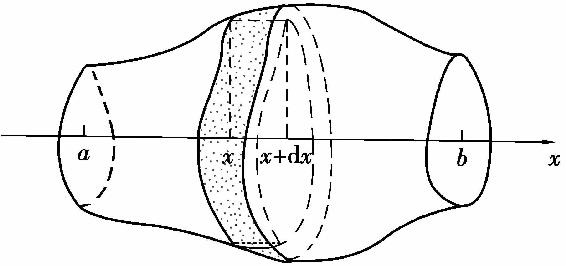
图5.13
立体中,相应于[a,b]上任一小区间[x,x+dx]的薄片的体积近似等于底面积为A(x)、高为dx的柱体的体积,即ΔV≈A(x)dx.由于A(x)连续,故在[x,x+dx]上有最大值M和最小值m,则
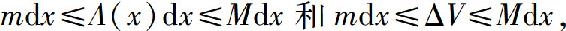
从而
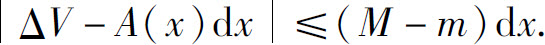
再由A(x)连续知,dx→0时M-m→0,所以
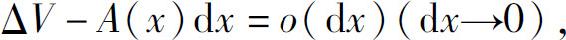
因此体积元素
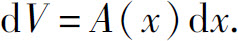
所求立体的体积

现在考虑旋转体.所谓旋转体,就是由一平面图形绕这平面内一条定直线旋转一周而成的立体.
设旋转体是由曲线y=f(x),直线x=a,x=b和x轴所围成的曲边梯形绕x轴旋转一周而成的立体,如图5.14所示.
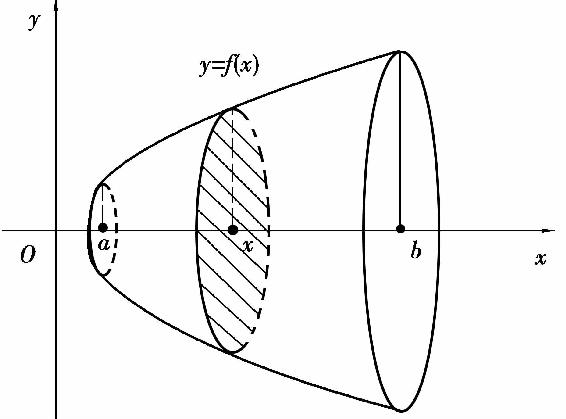
图5.14
此时,垂直于x轴的平面截立体之截面显然为一圆,圆心在x轴上点x处,半径r=y=f(x),截面面积为
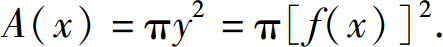
于是,所求旋转体体积为

类似可得,由曲线x=φ(y),直线y=c,y=d(c<d)与y轴所围成的曲边梯形绕y轴旋转一周而成的旋转体的体积为
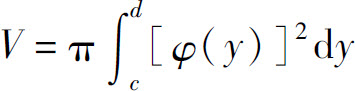
例5 计算椭圆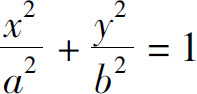 所围图形绕x轴旋转而成的旋转体的体积,如图5.15所示.
所围图形绕x轴旋转而成的旋转体的体积,如图5.15所示.
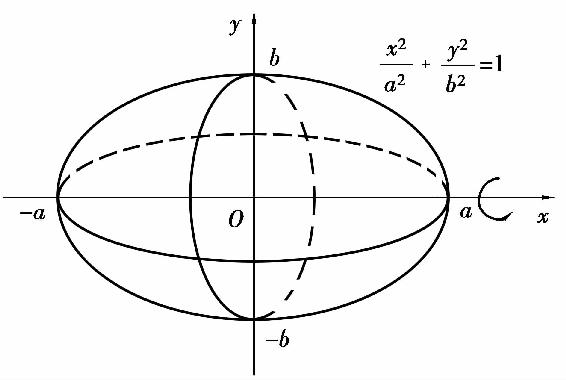
图5.15
解 旋转体实际上是由上半椭圆
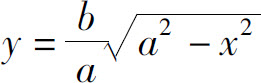
及x轴所围曲边梯形绕x轴旋转一周而成.所以,所求体积
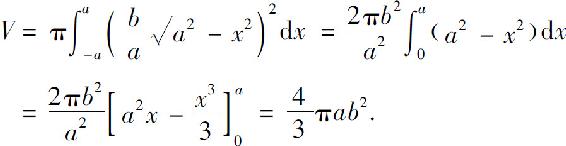
5.5.3 定积分在物理学上的应用
1)变力所作的功
如果常力F作用于某物体,使该物体沿力的方向作直线运动,设其移动的距离为s,则力F所作的功W为
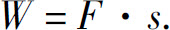
如果物体在运动过程中所受到的力是变化的,这就会遇到变力对物体作功的问题.下面通过具体例子说明如何计算变力所作的功.
例6 从地面垂直向上发射质量为m的火箭,问初速至少为多大时,火箭始能超出地球的引力范围.
解 设地球的半径为R,质量为M.根据万有引力定理,当火箭距地面的高度为x时,火箭受地球的引力为
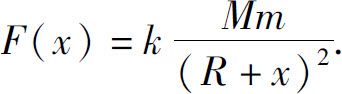
其中k为引力常数.为确定常数k,令x=0(地面),则F=mg,其中g为重力加速度,即
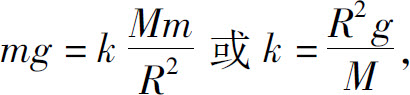
从而
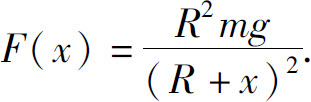
当火箭从x升高到x+dx时,地球引力对它所作的功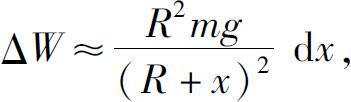 故功元素
故功元素
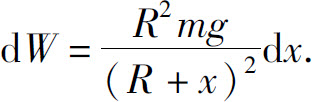
于是,当火箭距地面的高度为h时,地球引力所作的功
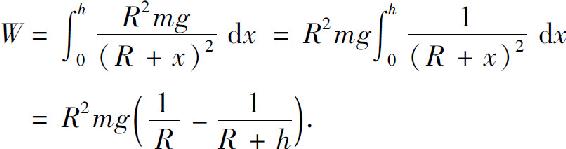
当h→+∞时,W→Rmg.若火箭离开地面的初速为v0,它具有动能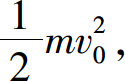 根据能量转换定律,为了使火箭超出地球引力范围,必须
根据能量转换定律,为了使火箭超出地球引力范围,必须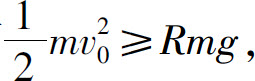 即
即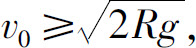 地球半径
地球半径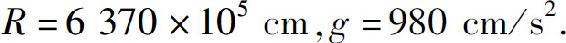 通过计算得v0≥11.2×105(cm/s).也就是说,为了使火箭超出地球引力范围,它的初速必须大于11.2km/s.
通过计算得v0≥11.2×105(cm/s).也就是说,为了使火箭超出地球引力范围,它的初速必须大于11.2km/s.
例7 有一个圆柱形贮水桶,高为5m,底圆半径为3m,桶内盛满了水.试问要把桶内的水全部吸出需要作多少功?
解 作x轴如图5.16所示,取深度x为积分变量,它的变化区间为[0,5].相应于[0,5]上的任一小区间[x,x+dx]的一薄层水的高度为dx.水的密度为1000kg/m3,这薄层水的重力为9800π·32dxN.这薄层水被吸出桶外需作的功ΔW≈88200π·x·dx,故功元素为
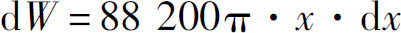
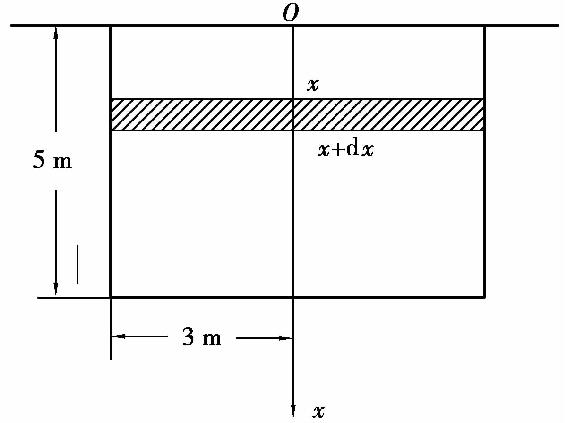
图5.16
于是所求的功为
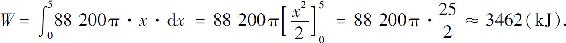
2)液体的静压力
从物理学知道,在液体深为h处的压强为p=ρgh,ρ是液体的密度.如果有一面积为A的平板水平地放置在液体深为h的地方,那么平板一侧所受的静压力为
P=p·A.
如果这个平板垂直放置在液体中,由于不同深处的压强p不相等,所以平板所受液体的静压力就不能用上述方法计算.
例8 一等腰梯形的闸门,上下底宽分别为10m和6m,高为20m,且上底位于水面,计算闸门一侧所受的水压力.
解 选择坐标系如图5.17所示,梯形两腰的方程为
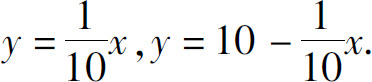
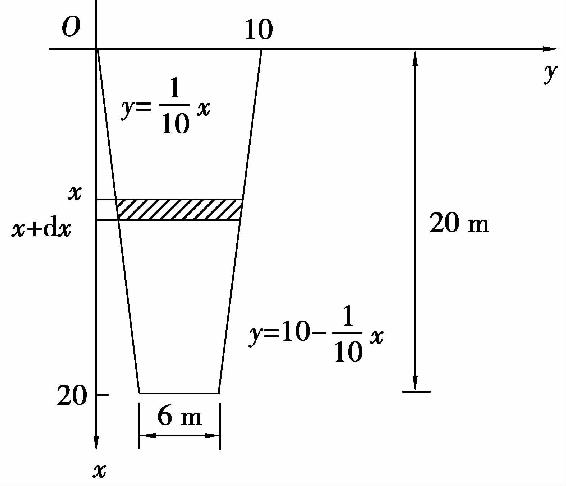
图5.17
相应于[0,20]上的任一小区间[x,x+dx]的小等腰梯形的面积近似于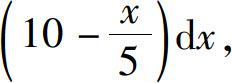 其上各点的压强近似于9800x(水的密度为1000kg/m3),于是所受水压力
其上各点的压强近似于9800x(水的密度为1000kg/m3),于是所受水压力
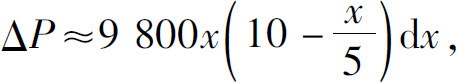
故压力元素为
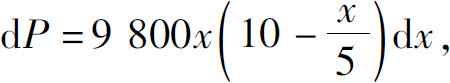
所以闸门一侧受到的水压力
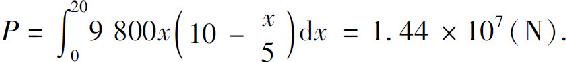
3)引力
从物理学知道,质量分别为m1,m2,相距为r的两质点间的引力大小为
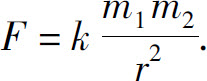
其中G为引力系数.如果要计算一根细棒对一个质点的引力,由于细棒上各点与该质点的距离是变化的,就不能用上述公式来计算.
例9 设有一长度为l,质量为M的均匀细棒,另有一质量为m的质点和细棒在一条直线上,质点到细棒近端的距离为a.试计算细棒对质点的引力.
解 选取坐标系如图5.18所示,以x为积分变量,它的变化区间为[0,l].任取一小区间[x,x+dx],细棒小段的质量为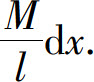 于是这一小段细棒对质点的引力
于是这一小段细棒对质点的引力
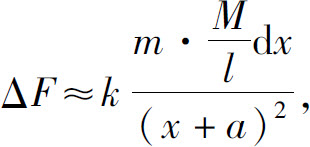

图5.18
故引力元素
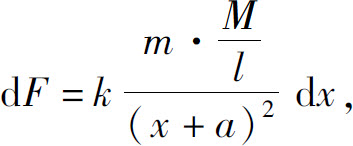
所以细棒对质点的引力
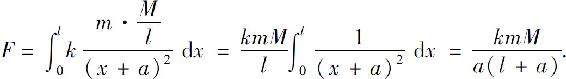
5.5.4 定积分在经济学上的应用
1)已知边际函数求总量函数
设固定成本为C0,边际成本为C′(Q),边际收益为R′(Q),其中Q为产量=需求量=销量,则总成本函数
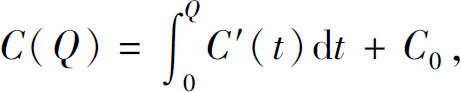
总收益函数
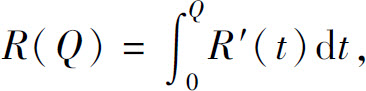
总利润函数
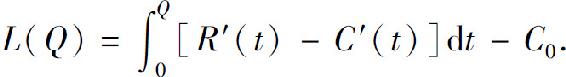
例10 若一企业生产某产品的边际成本是产量x的函数
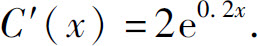
固定成本C0=90,求总成本函数.
解
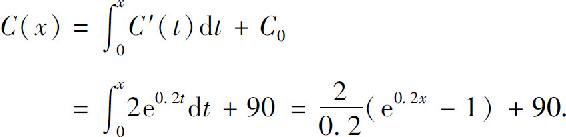
于是,所求总成本函数为
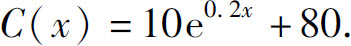
例11 设生产某产品x单位时的边际收入为
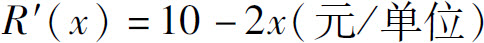
求生产40单位时的总收入及平均收入,并求再增加生产10单位时所增加的总收入.
解 利用积分上限函数的表示式,可直接求出
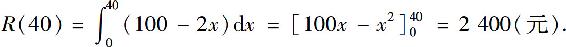
平均收入是
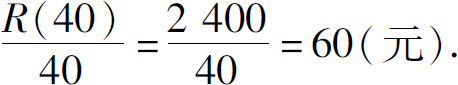
在生产40个单位后再生产10个单位所增加的总收入可由增量公式求得:
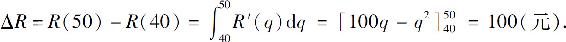
例12 已知某产品的边际收入R′(x)=25-2x,边际成本C′(x)=13-4x,固定成本C0=10,求当x=5时的毛利和纯利(毛利是包含固定成本的利润,而纯利即不包含固定成本的利润).
解 由边际利润的表达式,有
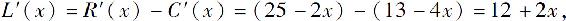
从而可求得当x=5时的毛利为
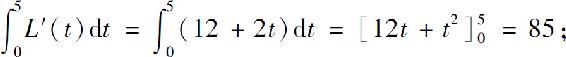
当x=5时的纯利为
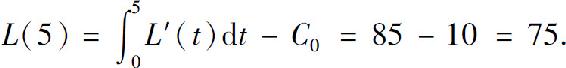
2)资金现值与投资问题
假设本金为A0元,年利率为r,存款期限为t年,t年后的本利和称为t年后的期末价值.
如按单利计息,t年后的期末价值为A0(1+tr);
如按复利计息,t年后的期末价值为A0(1+r)t;
如按连续复利计息,即将一年分为m次计算复利,且m→∞,则t年后的期末价值为
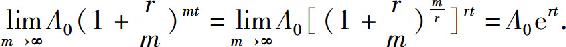
如果t年后的期末价值为a,其现值即贴现价值A0为多少?
设年利率为r,如按一年计算复利一次,a=A0(1+r)t,故a的贴现价值A0=a(1+r)-t;
如按连续复利计息,则A0=ae-rt.
如果收入或支出不是一次实现的,而是在每个时间周期内连续、均匀地收入或支出一个固定的数额a,则称此类收入或支出为均匀收支流,a称为收入或支出的流量.如果收入或支出的流量不是常数a,而是t的函数a(t),这时称为非均匀收支流.
设r表示一周期利率(若周期为年,r就是年利率)并按连续复利计息.这个收入(或支出)共延续了T个周期:
(1)如果按连续复利计息,在时间间隔[0,T]中总收入(或支出)的贴现价值为N,则
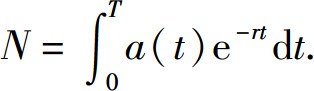
如果a(t)=a,则
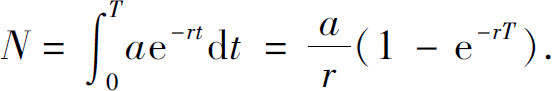
如有一笔投资I而得到一均匀的收入流a,则这笔投资产生的纯收入的贴现价值P为
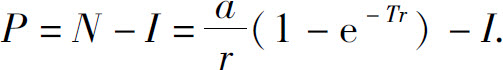
当N=I,表示投资回收了.故投资回收期有以下公式
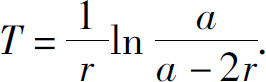
(2)如果按复利计息(非连续复利),则T期总收入的贴现价值
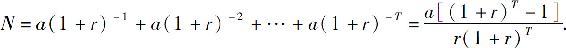
例13 设有一辆轿车,售价14万元.现某人分期支付购买,准备20年付清,按年利率5%的连续复利计息,问每年应支付多少元?
解 设每年付款数相同为a万元,T=20,全部付款的总现值(总贴现值)M=14(万元),r=0.05,于是,由
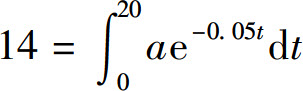
得a≈1.1006万元,即每年付款11006元.
例14 有一个大型投资项目,投资成本为A=10000(万元),投资年利率为5%,每年的均匀收入率a=2000(万元),求该投资为无限期时的纯收入的贴现值(或称为投资的资本价值).
解 由题设条件可知,收入率a=2000(万元),年利率r=5%,故无限期投资的总收入的贴现值为
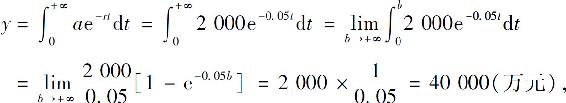
从而投资为无限期的纯收入贴现值为
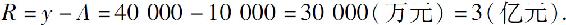
即投资为无限期的纯收入的贴现值为3亿元.
习题5.5
1.求由下列各曲线所围图形的面积:
(1)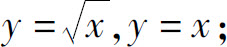
(2)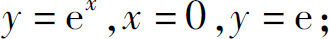
(3)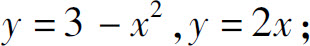
(4)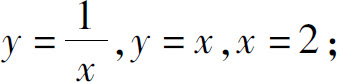
(5)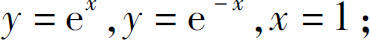
(6)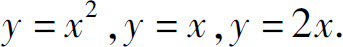
2.求由抛物线y=-x2+4x-3及其在点(0,-3)和(3,0)处的切线所围成图形的面积.
3.求由下列各曲线所围成图形的面积:
(1)r=2a cosθ(a>0);
(2)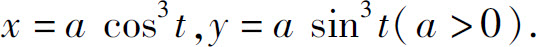
4.求下列各题中的曲线所围成平面图形绕指定轴旋转形成旋转体的体积:
(1)y=x3,y=0,x=2绕x轴、y轴;
(2)y=x2,x=y2绕y轴.
5.求曲线xy=a(a>0)与直线x=a,x=2a及x轴所围成的图形,绕x轴旋转一周产生的旋转体的体积.又若这图形绕y轴旋转,则体积为多少?
6.半径为2m的圆柱形水池中充满了水,现在要从池中吸出,使水面下降5m,问需要作多少功?
7.边长为a和b的矩形薄板,与液面成α(0°<α<90°)角斜沉于液体中.设a>b,长边平行于液面,上沿位于深h处,液体的比重为v,试求薄板一侧所受的静压力.
8.设有一长度m,质量为M的均匀直棒,在它的中垂线上距离为a单位处有一质量为m的质点,求该棒对质点的引力.
9.某产品需求量q是价格p的函数,最大需求量1000.已知边际需求为
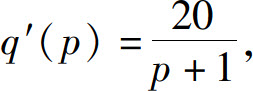
试求需求与价格的函数关系.
10.已知边际成本C′(q)=25+30q-9q2,固定成本为55,试求总成本C(q)及平均成本.
11.已知边际收入C′(q)=3-0.2q,q为销售量.求总收入函数R(q),并确定最高收入的大小.
12.已知某产品生产q单位时,总收益R的变化率(边际收益)为
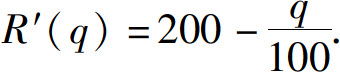
(1)求生产了50单位时的总收益;
(2)如果已经生产了100单位,求再生产100单位时的总收益.
