6.5 多元函数的极值
6.5 多元函数的极值
6.5.1 多元函数的极值
定义 设函数z=f(x,y)在点(x0,y0)的某个邻域内有定义,如果对于该邻域内异于(x0,y0)的任何点(x,y),都有
f(x,y)<f(x0,y0)(或f(x,y)>f(x0,y0)),
则称函数f(x,y)在点(x0,y0)取得极大值(或极小值).
极大值与极小值统称为极值,使函数取得极值的点(x0,y0)称为极值点.
例如,函数z=x2+y2在点(0,0)处取得极小值0.因为在点(0,0)处的函数值为0,而在点(0,0)的任一邻域内异于(0,0)的点的函数值都大于0.从几何上看也是明显的,因为点(0,0)是开口向上的旋转抛物面的z=x2+y2顶点.
如何寻找已知函数的极值点呢?我们首先要找到已知函数的可能极值点,即要研究函数取得极值的必要条件.
设函数f(x,y)在点(x0,y0)处取得极值,固定y=y0,则z=f(x,y0)是一元函数,它在x=x0处取极值,由一元可导函数取得极值的必要条件可知fx(x0,y0)=0.同理可有fy(x0,y0)=0.
定理1(极值的必要条件) 设函数f(x,y)在点(x0,y0)处取得极值,且函数在该点的两个偏导数存在,则
fx(x0,y0)=0, fy(x0,y0)=0.
与一元函数类似,把同时满足fx(x0,y0)=0,fy(x0,y0)=0的点(x0,y0)称为函数f(x,y)的驻点.由定理1可知,偏导数存在的函数极值点一定是驻点.但是驻点不一定是极值点,例如,点(0,0)是函数z=x2-y2的驻点,但不是它的极值点.
以上二元函数极值的概念与结论可推广到三元及三元以上的多元函数.
那么,什么条件下驻点一定是极值点呢?可以证明如下定理:
定理2(极值的充分条件) 设z=f(x,y)在点(x0,y0)的某个邻域内有连续二阶偏导数,且点(x0,y0)是函数的驻点.记
A=fxx(x0,y0), B=fxy(x0,y0), C=fyy(x0,y0)
则
(1)当AC-B2>0时,点(x0,y0)是极值点,且A<0时,点(x0,y0)是极大值点;A>0时,点(x0,y0)是极小值点;
(2)当AC-B2<0时,点(x0,y0)不是极值点;
(3)当AC-B2=0时,点(x0,y0)可能是极值点,也可能不是极值点.
例1 求函数f(x,y)=x2+2xy+2y2+4x+2y-5的极值.
解 解方程组
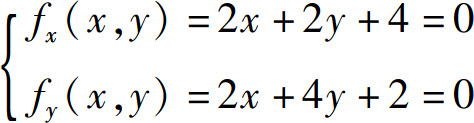
得x=-3,y=1.点(-3,1)是函数的驻点.
再求二阶偏导数,得
fxx(x,y)=2, fxy(x,y)=2, fyy(x,y)=4
都是常数,于是有
AC-B2=2·4-22=4>0
而A=2>0,所以函数f(x,y)在点(-3,1)处取极小值,其值为f(-3,1)=-10.
例2 求函数f(x,y)=xy(1-x-y)的极值.
解 解方程组
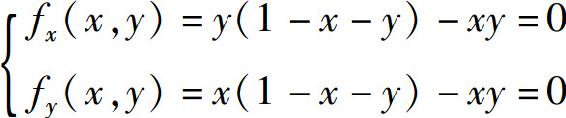
易得驻点(0,0),(1,0),(0,1),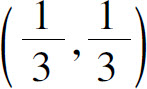 .
.
再求二阶偏导数:
fxx(x,y)=-2y,fxy(x,y)=1-2x-2y,fyy(x,y)=-2x.
在点(0,0)处
AC-B2=0·0-12=-1<0,
所以点(0,0)不是f(x,y)的极值点;
在点(1,0)处
AC-B2=0·(-2)-(-1)2=-1<0,
所以点(1,0)不是f(x,y)的极值点;
在点(1,0)处
AC-B2=(-2)·0-(-1)2=-1<0,
所以点(1,0)不是f(x,y)的极值点;
在点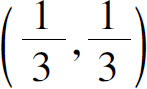 处
处
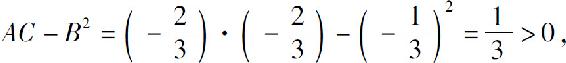
所以点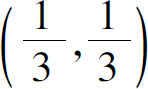 是f(x,y)的极值点,又因为
是f(x,y)的极值点,又因为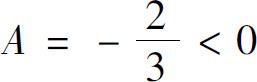 ,所以f(x,y)在点
,所以f(x,y)在点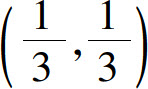 处取得极大值
处取得极大值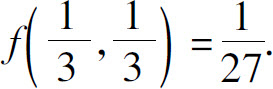
应当注意,除了驻点外,偏导数不存在的点也可能是极值点.例如,由定义可知函数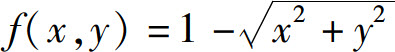 在点(0,0)处取得极大值1,但点(0,0)并不是驻点,因为fx(0,0),fy(0,0)都不存在.
在点(0,0)处取得极大值1,但点(0,0)并不是驻点,因为fx(0,0),fy(0,0)都不存在.
6.5.2 多元函数的最值
与一元函数类似,可以利用函数的极值求函数的最大值和最小值.
如果函数z=f(x,y)在有界闭区域D上连续,则由连续函数的最值定理可知f(x,y)在D上必存在最大值和最小值.又设f(x,y)在D上存在偏导数,如果最大值和最小值在D的内部取得,那么这些最大值点或最小值点必然是驻点.所以将函数f(x,y)在D的内部的所有驻点处、偏导数不存在点处的函数值及在D的边界上的最大值和最小值相互比较,其中最大的就是f(x,y)在D上的最大值,最小的就是最小值.
例3 求函数f(x,y)=x2+2y2-x在闭区域D={(x,y)|x2+y2≤1}上的最大值和最小值.
解 函数在有界闭区域D上连续,故一定有最大值和最小值.
先求驻点.解方程组
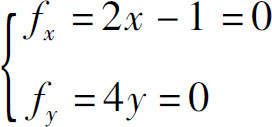
得唯一驻点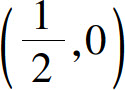 .
.
再求在D的边界x2+y2=1上的可能最值点.
在边界x2+y2=1上,函数
f(x,y)=x2+2y2-x
成为
f(x,y)=x2+y2+y2-x=2-x2-x.
故转化为求函数
g(x)=2-x2-x
在[-1,1]上的可能最值点.
令g′(x)=0得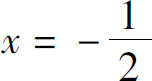 ,可能最值点为x1=-1,
,可能最值点为x1=-1,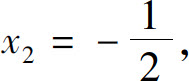 x3=1.对应f(x,y)在边界上的可能最值点为(-1,0),
x3=1.对应f(x,y)在边界上的可能最值点为(-1,0),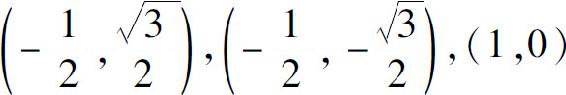 .
.
最后,比较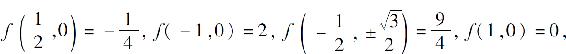 得所求最大值为
得所求最大值为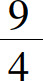 ,最小值为
,最小值为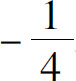 .
.
在实际问题中,如果知道目标函数f(x,y)在定义域D内一定能取得最大值(或最小值),且在D内有唯一驻点,则可以肯定函数在该点取得最大值(或最小值).
例4 要做一个容积为V的长方体无盖容器,问如何选取长、宽、高才能使用料最省?
解 设容器的长为x,宽为y,则高为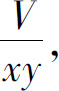 因此容器的表面积
因此容器的表面积
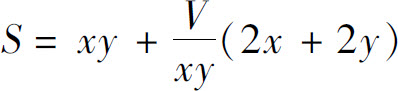
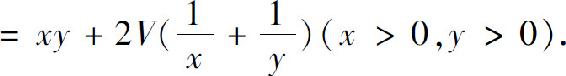
解方程组
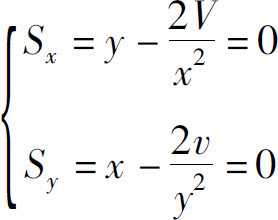
得函数S(x,y)的唯一驻点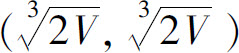 .
.
根据题意可知,表面积S的最小值是存在的,所以函数的唯一驻点就是最小值点,即当容器长、宽、高分别为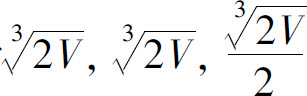 时用料最省.
时用料最省.
6.5.3 条件极值
有些极值问题,对于函数自变量,除了限制在定义域内,还受其他附加条件的约束,这类极值称为条件极值.
求解条件极值问题的一种方法是将条件极值转化为无条件极值.例如,例4中,如果设容器的长、宽、高分别为x,y,z,则容器的表面积S=xy+(2x+2y)z,此时还有一个约束条件xyz=V,这是条件极值问题.例4的解法是通过从约束条件xyz=V中解出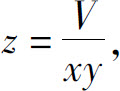 代入S=xy+(2x+2y)z使之成为一个无条件极值问题.但是条件极值化为无条件极值并不是都能实现的,即使能实现,有时问题并不简单.下面介绍一种直接求条件极值的方法.
代入S=xy+(2x+2y)z使之成为一个无条件极值问题.但是条件极值化为无条件极值并不是都能实现的,即使能实现,有时问题并不简单.下面介绍一种直接求条件极值的方法.
拉格朗日乘数法 求函数z=f(x,y)在条件φ(x,y)=0下的极值的步骤:
(1)作拉格朗日函数
L(x,y)=f(x,y)+λφ(x,y).
其中λ是待定常数,称为拉格朗日乘数.
(2)求L(x,y)对x与y的一阶偏导数,并令它们为0,然后与φ(x,y)=0联立
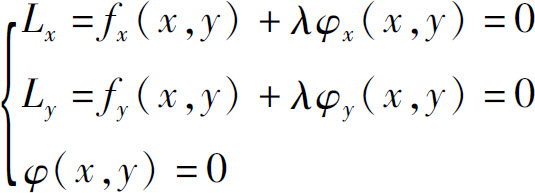
(3)由方程组解出x,y,λ,所得的点(x,y)就是函数z=f(x,y)在φ(x,y)=0条件下可能的极值点.
对于三元及三元以上函数或多于一个约束条件的情形,有类似的结果.
例5 用拉格朗日乘数法求解例4.
解 设容器的长、宽、高分别为x,y,z,所求问题化归为求目标函数
S=xy+2(x+y)z (x>0,y>0,z>0)
在条件 φ(x,y,z)=xyz-V=0
下的最小值问题.
作拉格朗日函数
L(x,y,z)=xy+2(x+y)z+λ(xyz-V),
令Lx=Ly=Lz=0,解方程组
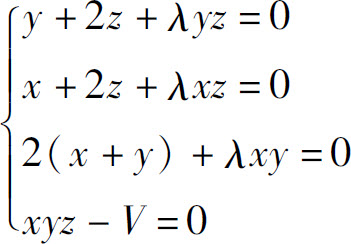
得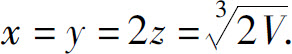
根据题意,S在条件φ(x,y,z)=0下确实存在最小值.所以当容器长、宽、高分别为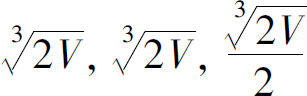 时,用料最省.
时,用料最省.
例6 经济学中有Cobb-Douglas生产函数模型
f(x,y)=Cxαyβ.
其中,x表示投入的劳动量,y表示投入的资本量,C与α,β(0<a,β<1)是常数,由不同企业的具体情况决定,函数值表示产量.
现已知某生产商的Cobb-Douglas生产函数为
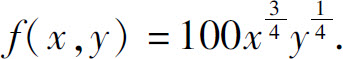
其中,每个劳动力与每单位资本的成本分别为150元与250元,该生产商的总预算是50000元,问该如何分配这笔钱用于雇用劳动力及投入资本,使产量最高?
解 问题即求目标函数
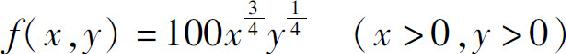
在约束条件
150x+250y=50000
下的最大值.
作拉格朗日函数
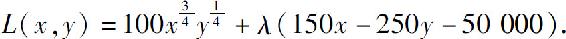
令Lx=Ly=0,解方程组
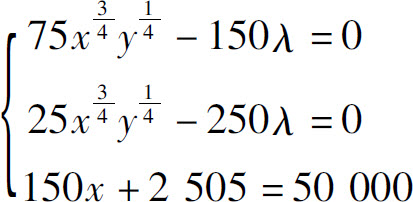
得x=250,y=50.
这是目标函数的唯一驻点,而由问题本身可知最高产量一定存在.故生产商雇用250个劳动力及投入50个单位资本时,可使产量最高.
习题6.5
1.求下列函数的极值:
(1)f(x,y)=4(x-y)-x2-y2;
(2)f(x,y)=xy+x2+y2;
(3)f(x,y)=e2x(x+2y+y2).
2.求下列函数在指定条件下的极值:
(1)z=xy,若2x+y=1;
(2)z=x-2y,若x2+y2=1;
(3)u=x+y+z,若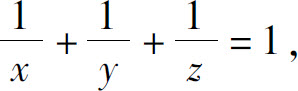 x>0,y>0,z>0.
x>0,y>0,z>0.
3.要制造一个无盖的圆柱形容器,其容积为V,要求表面积A最小,问容器的高度H和半径R应为多少?
4.在椭圆上x2+4y2=4求一点,使其到直线2x+3y-6=0距离最短.
5.已知矩形的周长为2P,将它绕其一边旋转而构成一立体,求所得立体体积最大的那个矩形.
6.求函数f(x,y)=e-xy在闭区域D={(x,y)|x2+4y2≤1}上的最大值和最小值.
7.某公司可通过电台及报纸两种方式做销售某商品的广告.根据统计资料,销售收入R(万元)与电台广告费用x1(万元)及报纸广告费用x2(万元)之间的关系有如下的经验公式: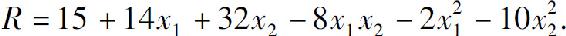
(1)在广告费用不限的情况下,求最优广告策略.
(2)若提供的广告费用为1.5万元,求相应的最优广告策略.
