4.2 换元积分法
4.2 换元积分法
利用基本积分公式与积分的性质所能计算的不定积分是十分有限的.本节把复合函数的微分法反过来用,得到一种基本的积分方法——换元积分法.
4.2.1 第一类换元积分法
设所求的不定积分为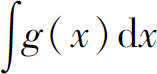 ,它可以写成
,它可以写成
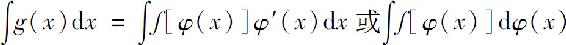
的形式,作代换u=φ(x),则上面的不定积分就化为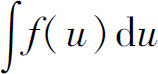 .如果容易求得f(u)的一个原函数F(u),则
.如果容易求得f(u)的一个原函数F(u),则
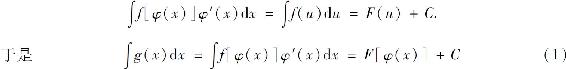
利用复合函数的求导公式,容易验证公式(1)的正确性.事实上,由
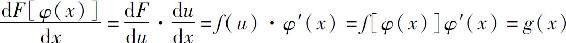
可知式(1)成立.利用公式(1)计算不定积分的方法称为第一类换元积分法,习惯上也称为凑微分法.
例1 求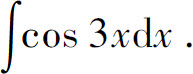
解 设u=3x,则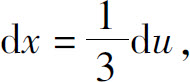 所以
所以
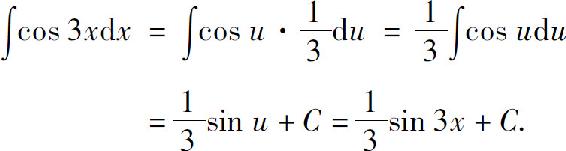
例2 求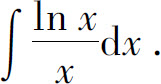
解 令u=lnx,则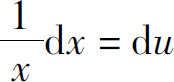 ,所以
,所以
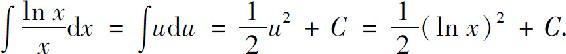
比较熟练后,可不写出变量代换过程,直接凑微分进行计算.如本例求解过程可简化如下:
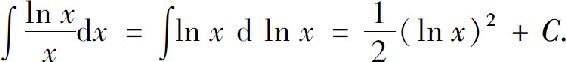
例3 求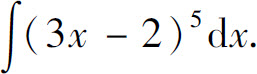
解 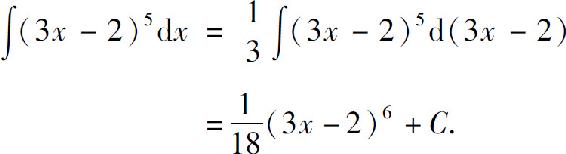
例4 求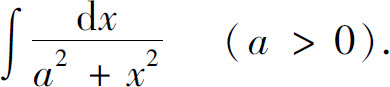
解
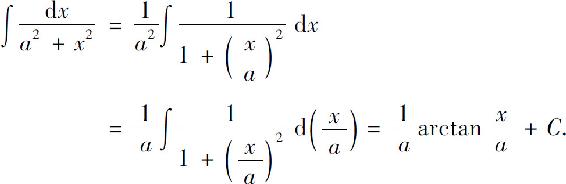
例5 求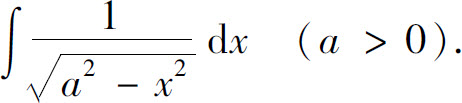
解
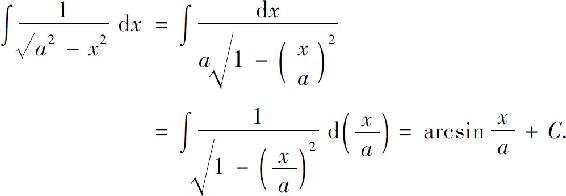
例6 求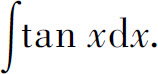
解
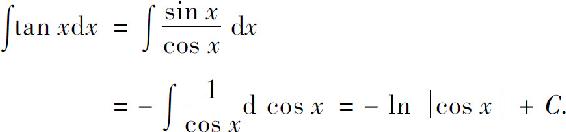
类似可求得
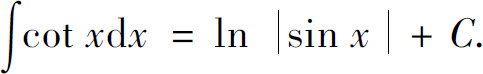
例7 求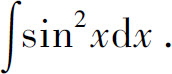
解
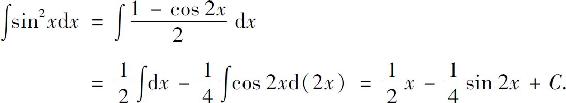
例8 求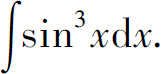
解
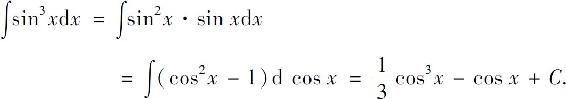
例9 求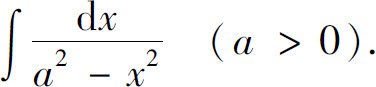
解 因为
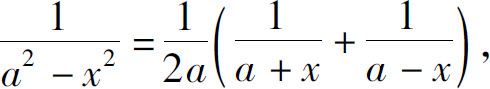
所以
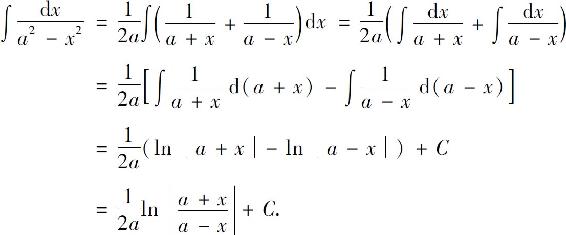
例10 求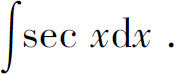
解
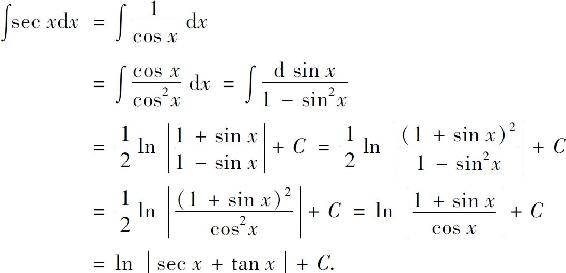
类似可求得 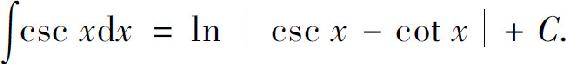
从以上例子可看出,积分运算与微分运算相比具有更大的灵活性.一般地,如果所遇到的不定积分能化为下列形式之一时,可考虑用换元积分法进行计算.
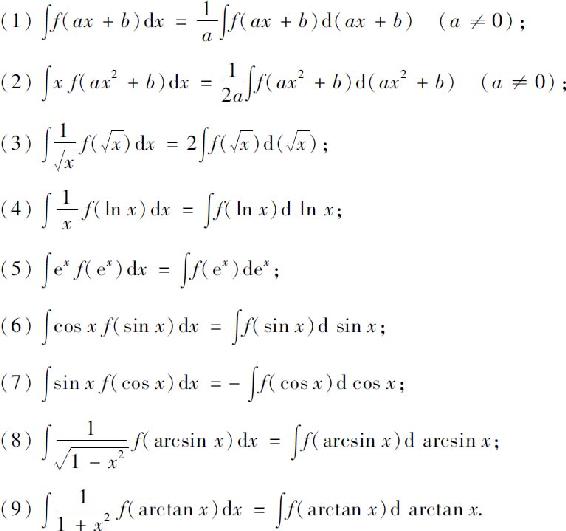
这里只要不定积分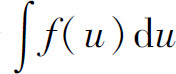 容易求得,所给的不定积分也就得到了.
容易求得,所给的不定积分也就得到了.
对于被积函数中含有根式的某些不定积分,也可以利用换元积分法进行求解,但不同的是,求解这类问题的主要原则是通过引进新变量,将被积函数中的根号去掉,即作另一种形式的变量代换x=φ(t).
4.2.2 第二类换元积分法
设所求的不定积分为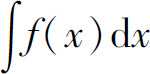 ,适当地选择变量代换x=φ(t),将积分
,适当地选择变量代换x=φ(t),将积分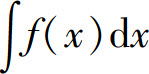 化为
化为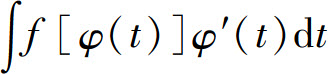 ,即
,即
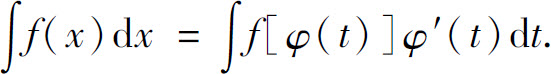
如果f[φ(t)]φ′(t)的一个原函数为Φ(t),则将t=φ-1(x)代入,得到f(x)的原函数Φ[φ-1(x)].这种换元法一般可写为:
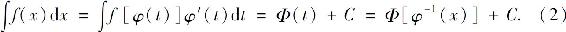
这里要求x=φ(t)单调可导,且φ′(t)≠0.
事实上,由复合函数的求导公式,有
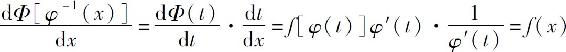
所以式(2)成立.利用公式(2)计算不定积分的方法称为第二类换元积分法.
如果被积函数中含有x的二次根式,可以考虑利用三角恒等关系,通过三角代换来去掉根式.
例11 求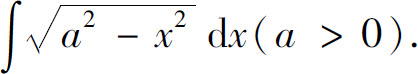
解 为了去掉被积函数中的根号,考虑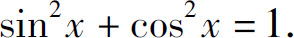
设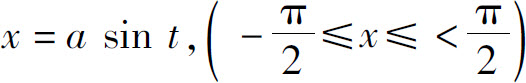 ,则
,则
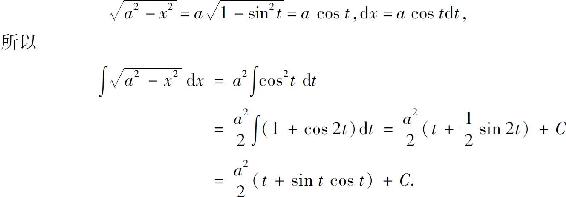
由于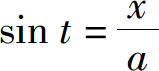 ,所以
,所以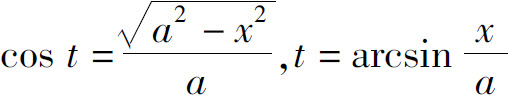 ,因此有
,因此有
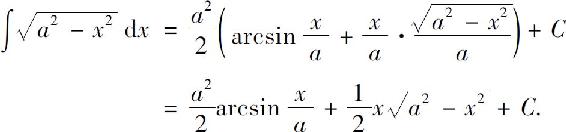
例12 求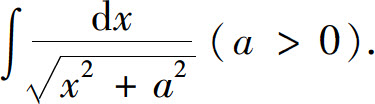
解 利用公式: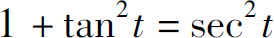 化去根号.
化去根号.
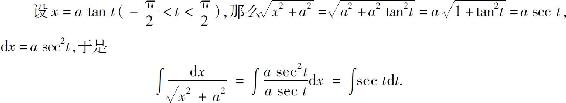
利用例8的结果得
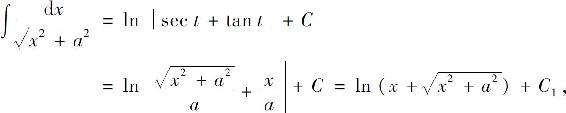
其中C1=C-ln a.
例13 求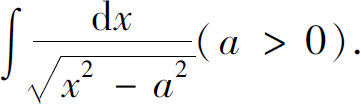
解 利用公式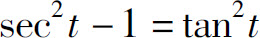 来化去根号.注意到被积函数的定义域是(a,+∞)和(-∞,-a)两个区间,在两个区间内分别求不定积分.
来化去根号.注意到被积函数的定义域是(a,+∞)和(-∞,-a)两个区间,在两个区间内分别求不定积分.
当x>a时,设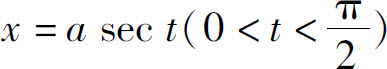 ,那么
,那么
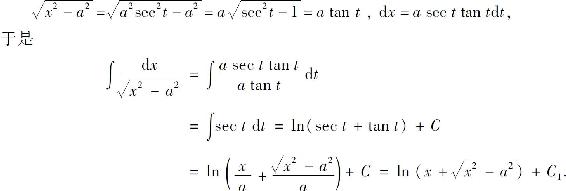
其中C1=C-ln a.
当x<-a时,令x=-u,那么u>a,由以上结果,有
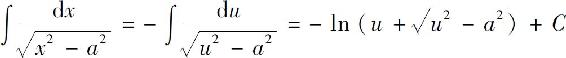
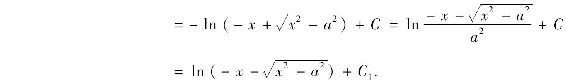
其中C1=C-2 ln a.
把x>a及x<-a的结果合起来,可写作
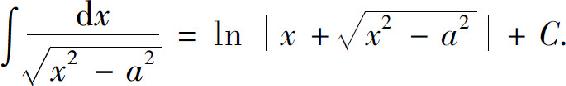
从以上三个例子可以看到,如果被积函数中含有因式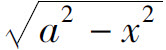 ,则可设x=a sint;如果被积函数中含有因式
,则可设x=a sint;如果被积函数中含有因式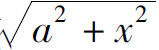 ,则可设x=a tant;如果被积函数中含有因式
,则可设x=a tant;如果被积函数中含有因式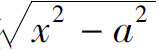 ,则可作变换x=a sec t.具体解题时要分析被积函数的具体情况,灵活采用各种变换与方法.
,则可作变换x=a sec t.具体解题时要分析被积函数的具体情况,灵活采用各种变换与方法.
例14 求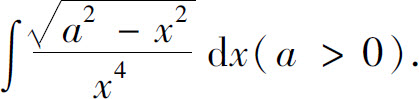
解 可通过三角代换来计算.这里采用倒代换,即设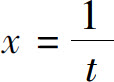 ,则
,则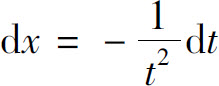 ,于是
,于是
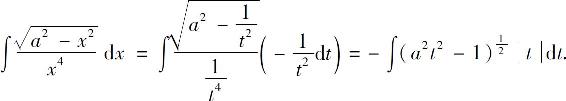
当x>0时,有
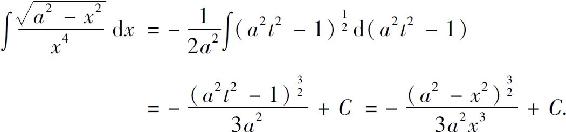
当x<0时,有相同结果.
例15 求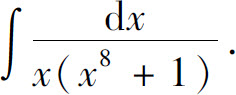
解 设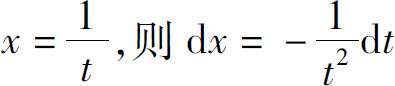 ,于是
,于是
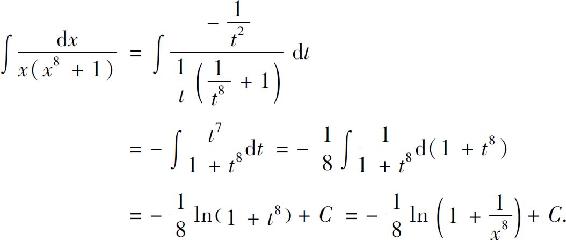
例16 求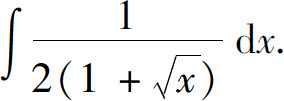
解 为了去掉被积函数中的根号,令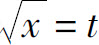 ,即x=t2,则dx=2tdt,所以
,即x=t2,则dx=2tdt,所以
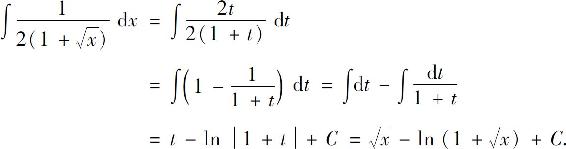
例17 求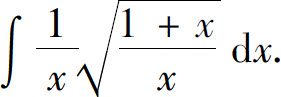
解 令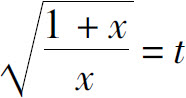 ,即
,即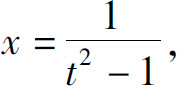 则
则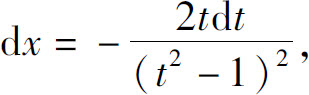 所以
所以
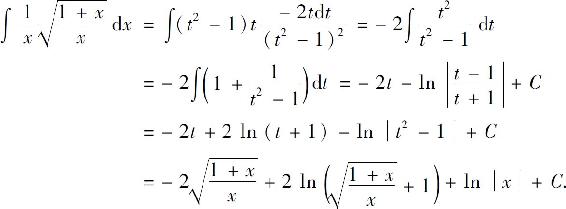
在本节的例题中,有几个积分以后经常会遇到,可当作公式使用(其中常数a>0):
(14)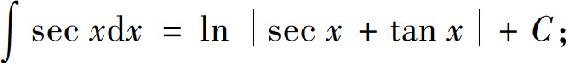
(15)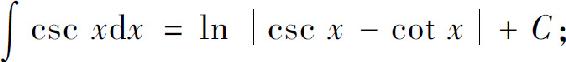
(16)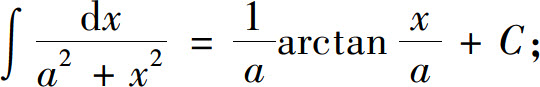
(17)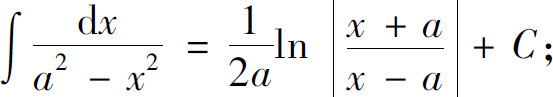
(18)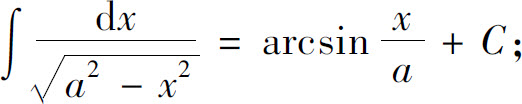
(19)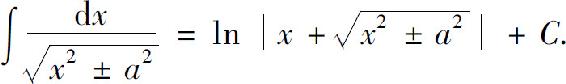
习题4.2
1.求下列不定积分:
(1)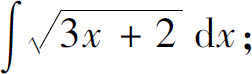
(2)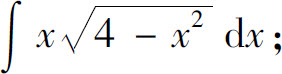
(3)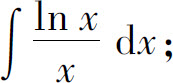
(4)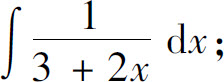
(5)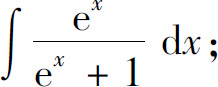
(6)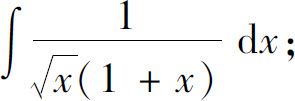
(7)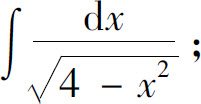
(8)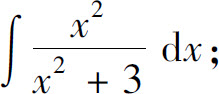
(9)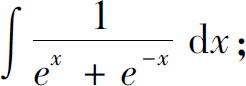
(10)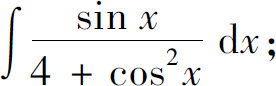
(11)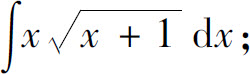
(12)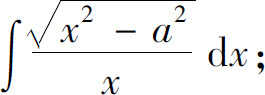
(13)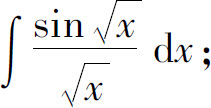
(14)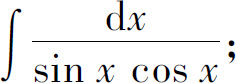
(15)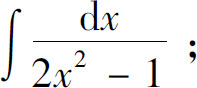
(16)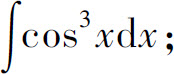
(17)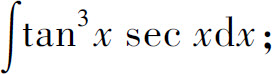
(18)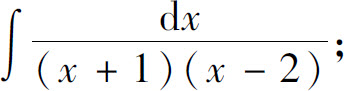
(19)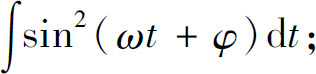
(20)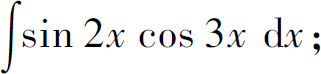
(21)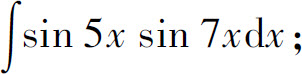
(22)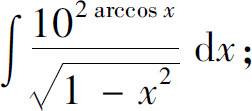
(23)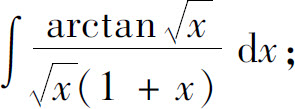
(24)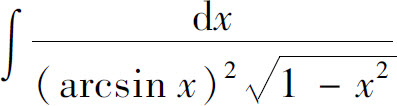
(25)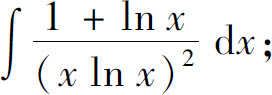
(26)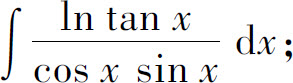
(27)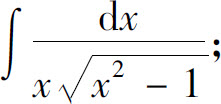
(28)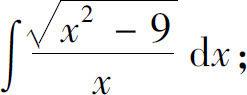
(29)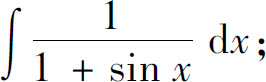
(30)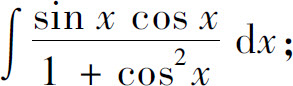
(31)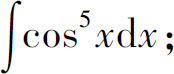
(32)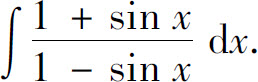
2.求下列不定积分:
(1)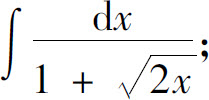
(2)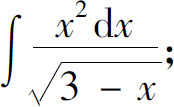
(3)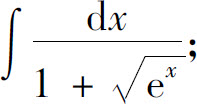
(4)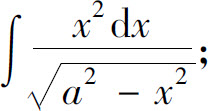
(5)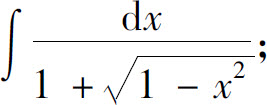
(6)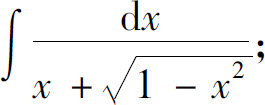
(7)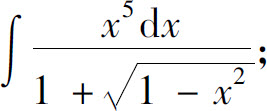
(8)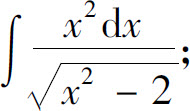
(9)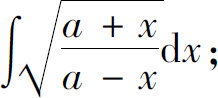
(10)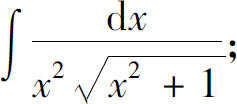
(11)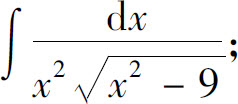
(12)