8.3　交错级数、绝对收敛与条件收敛

8.3　交错级数、绝对收敛与条件收敛

上节介绍的收敛判别法仅适用于正项级数．本节讨论带负项的级数，其中简单而重要的一类是交错级数．

8.3.1　交错级数

如果一个级数的各项是正负交错的，即形如

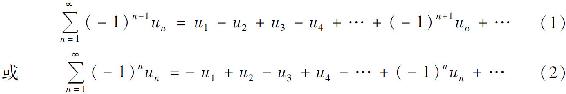
其中un＞0（n＝1，2，…），则称该级数为交错级数．

因为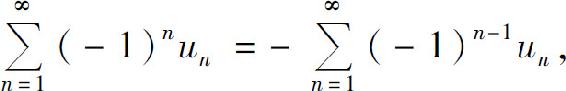所以只讨论形如（1）的交错级数．

关于交错级数，有如下判别法：

定理1（莱布尼茨判别法）　如果交错级数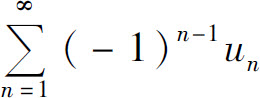满足条件

（1）

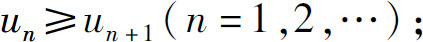
（2）

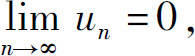
则级数收敛，且其和s≤u1．

证　级数的前2n项部分和

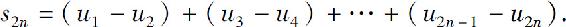
由条件（1）知所有括号内的差都是非负的，因而数列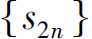是单调增加的．另一方面，s2n也可以写成

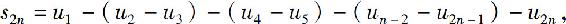
同样由条件（1）知所有括号内的差都是非负的，因而s2n≤u1，即数列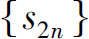有界．于是，根据单调有界准则可知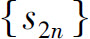，有极限s，且s≤u1，即

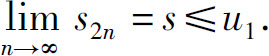
级数的前2n＋1项部分和

s2n＋1＝s2n＋u2n＋1．

由条件（2）知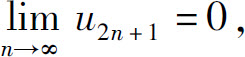因而

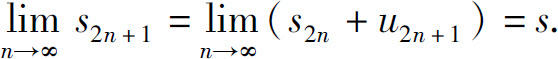
由此可见，级数的前2n项部分和与前2n＋1项部分和趋于同一极限s，故级数的部分和数列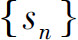有极限s．这就证明了所给级数收敛于和s，并且s≤u1．

例1　讨论交错级数

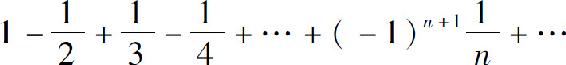
的收敛性．

解　这里

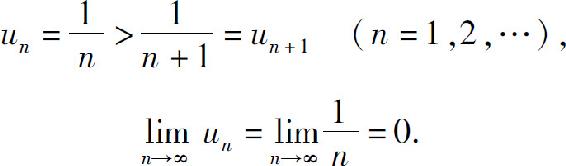
由莱布尼茨判别法知级数收敛．

8.3.2　绝对收敛与条件收敛

现在来讨论一般的级数

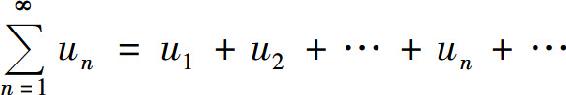
它的各项是任意实数，其收敛性通常可以借助把它的各项取绝对值后所得的正项级数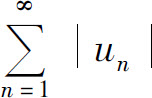的收敛性来讨论．

定理2　如果级数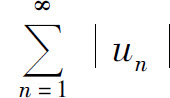收敛，则级数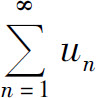必收敛．

证　因为

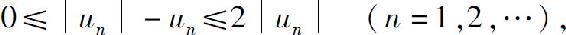
由比较判别法知，正项级数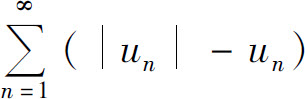收敛．而级数

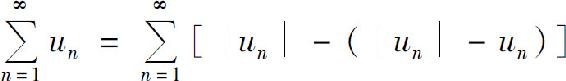
是两个收敛级数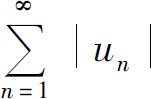与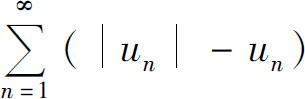的差，所以级数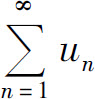收敛．

定理表明，对于一般的级数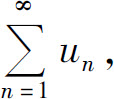如果用正项级数的判别法判定级数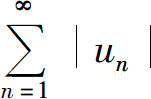收敛，则级数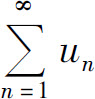一定收敛．但如果级数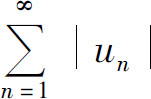发散，则不能判定级数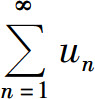也发散．例如，例1中的级数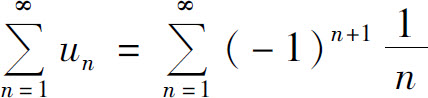是收敛的，而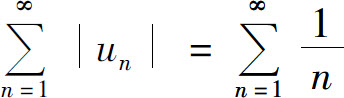为调和级数，是发散的．

定义　如果级数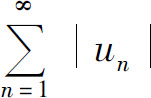收敛，则称级数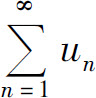绝对收敛；如果级数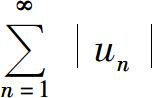发散，而级数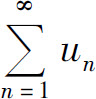收敛，称级数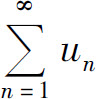条件收敛．

所以，判断一般项级数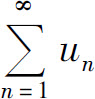的收敛性，可以先考虑各项取绝对值后的正项级数的收敛性．若级数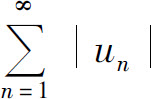收敛，则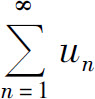本身一定收敛．若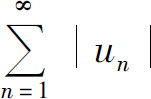发散，则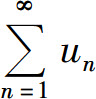的收敛性未知，还需再用其他方法讨论级数本身的收敛性．

例2　讨论级数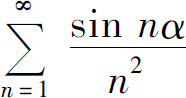的收敛性．

解　因为

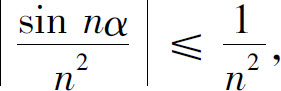
而级数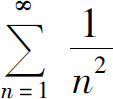收敛，所以所给级数绝对收敛，因而收敛．

例3　讨论级数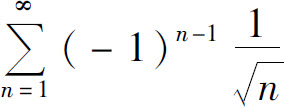的收敛性．

解

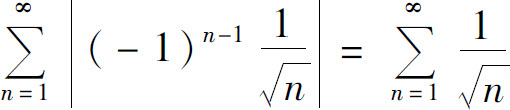
为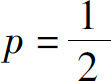的p级数，是发散的．但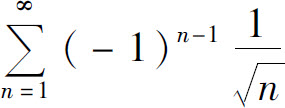是交错级数，满足

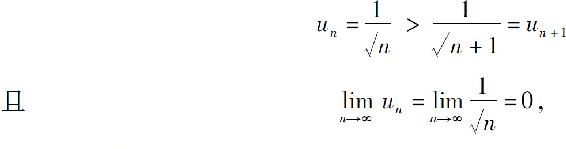
所以级数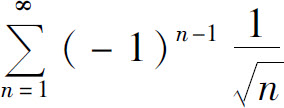收敛，且条件收敛．

习题8.3

1．下列交错级数哪些收敛？哪些发散？

（1）

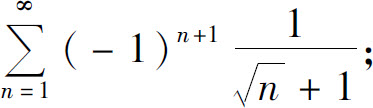
（2）

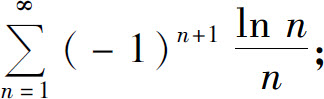
（3）

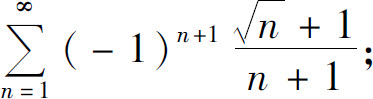
（4）

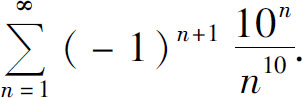
2．判定下列级数是否收敛？如果收敛，是绝对收敛还是条件收敛？

（1）

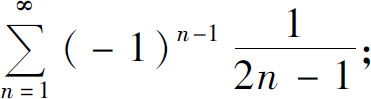
（2）

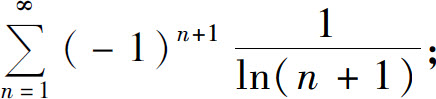
（3）

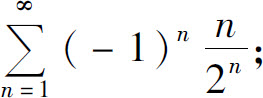
（4）

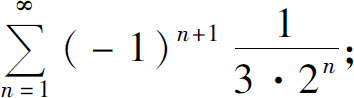
（5）

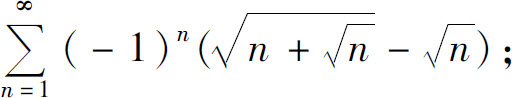
（6）

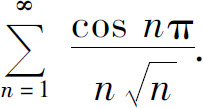
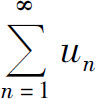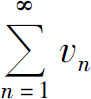3．举例说明即使与都收敛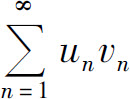，也可能发散．