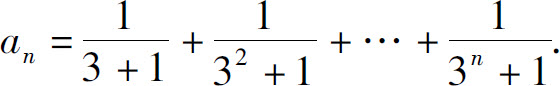1.4 极限存在准则 两个重要极限
1.4 极限存在准则 两个重要极限
本节介绍极限存在的两个准则,并在此基础上讨论两个重要极限: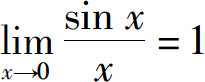 及
及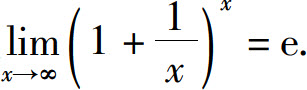
1.4.1 极限存在准则
1)夹逼准则
定理1 如果数列{an},{bn},{cn}满足:
(1)存在正整数N,当n>N时,有an≤cn≤bn;
(2)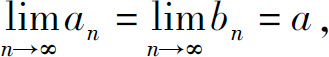
则数列{cn}收敛,且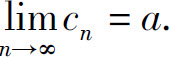
证 由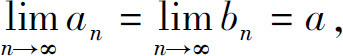 故对任给ε>0,分别存在正整数N1与N2,使得当n>N1时有
故对任给ε>0,分别存在正整数N1与N2,使得当n>N1时有
a-ε<an<a+ε;
当n>N2时有
a-ε<bn<a+ε.
取N3=max{N,N1,N2},则当n>N3时,有
a-ε<an≤cn≤bn<a+ε,
即
∣cn-a∣<ε,
所以
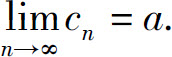
这个定理不仅给出了判定数列收敛的一种方法,而且也提供了一种求极限的方法.
例1 设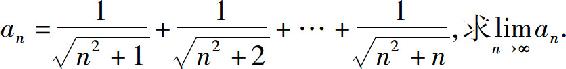
解 由于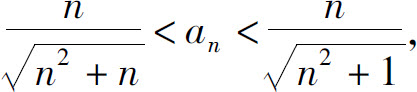 而
而
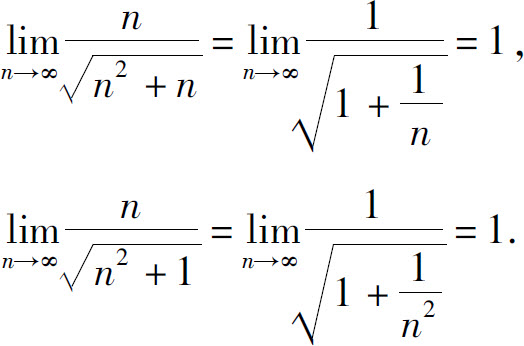
由夹逼准则知
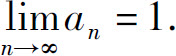
上述数列极限存在准则可以推广到函数极限的情形.
定理2 如果函数f(x),h(x),g(x)满足:
(1)在x0的某个去心邻域内,f(x)≤h(x)≤g(x);
(2)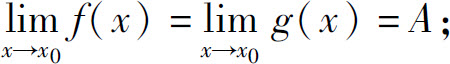
则
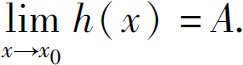
例2 求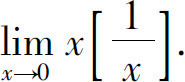
解 由于
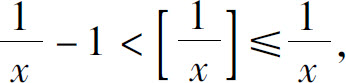
当x>0时
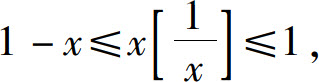
而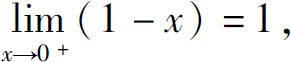 故由夹逼准则得
故由夹逼准则得
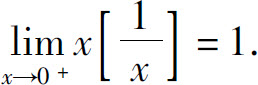
另一方面,当x<0时
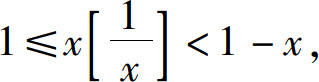
而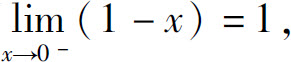 故由夹逼准则得
故由夹逼准则得
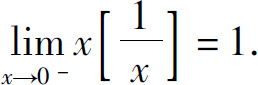
综上所述,得
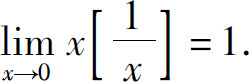
2)单调有界准则
定义 如果数列{an}满足
a1≤a2≤…≤an≤an+1≤…
则称{an}是单调增加数列;如果数列{an}满足
a1≥a2≥…≥an≥an+1≥…
则称{an}是单调减少数列.单调增加和单调减少数列统称为单调数列.
定理3(单调有界准则) 单调有界数列必有极限.
例3 设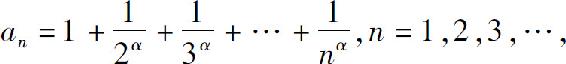 其中实数α≥2,证明:数列{an}收敛.
其中实数α≥2,证明:数列{an}收敛.
证 显然{an}是单调增加的,下面证明{an}有上界.事实上
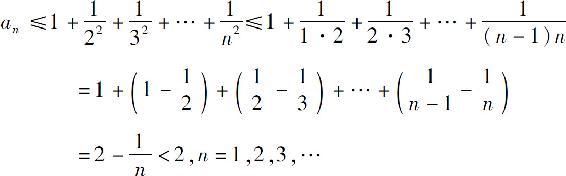
于是,由单调有界准则,数列{an}收敛.
例4 证明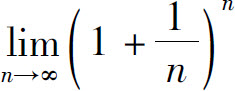 存在.
存在.
证 由于
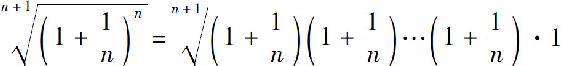
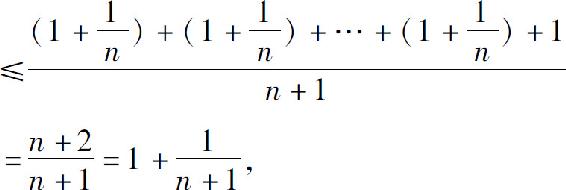
所以
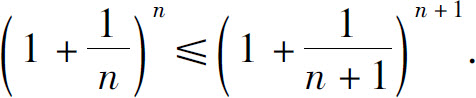
因此,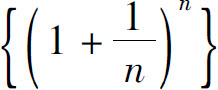 单调增加.
单调增加.
因为
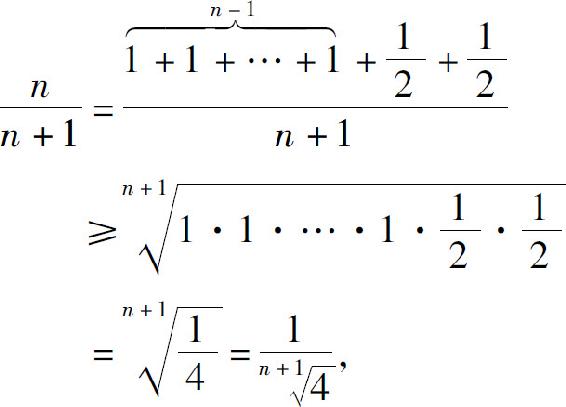
故
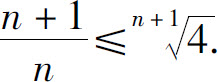
从而
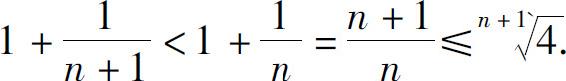
即
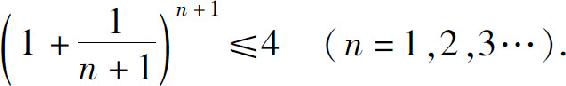
所以对一切n,有an<4.故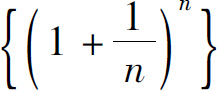 有上界.
有上界.
由单调有界准则知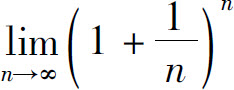 存在.通常用拉丁字母e表示该极限,即
存在.通常用拉丁字母e表示该极限,即
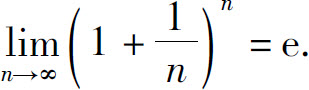
e是一个无理数,它的值是
e≈2.718 281 828 459…
1.4.2 两个重要极限
(1)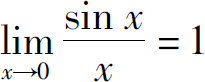
在如图1.13所示的单位圆内,当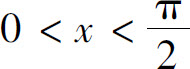 时,显然有
时,显然有
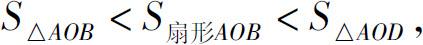
即
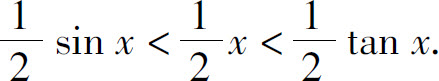
故
sin x<x<tan x.
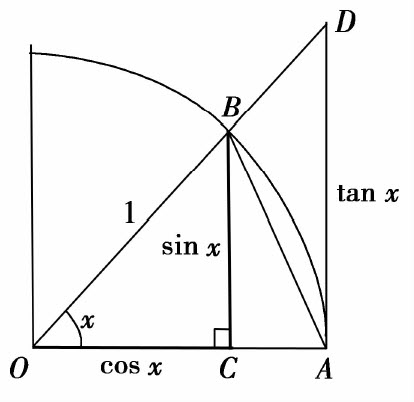
图1.13
不等式各边同除以sin x,有
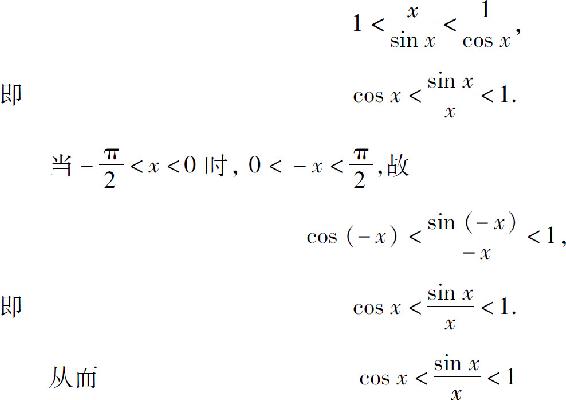
对一切满足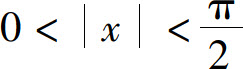 的x都成立.
的x都成立.
由于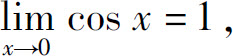 由夹逼准则得
由夹逼准则得
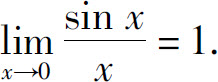
例5 计算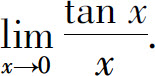
解 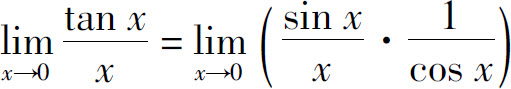
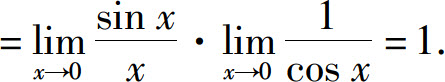
例6 计算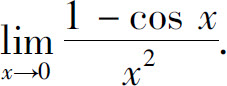
解
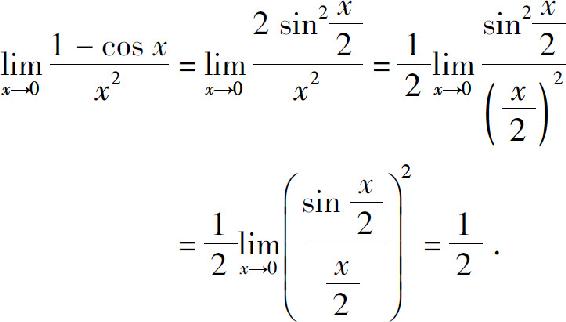
2)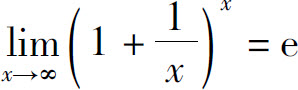
证 先考虑x→+∞的情形.任意x≥1,有
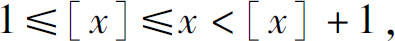
故
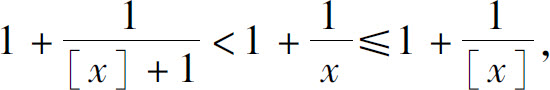
则
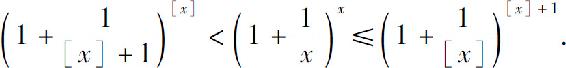
由例4有
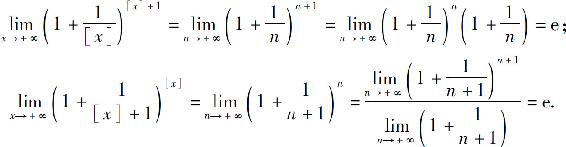
由夹逼准则有
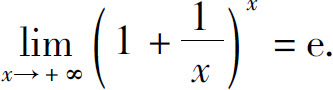
再证x→-∞的情形.当x<0时,设x=-y,则x→-∞时y→+∞,故
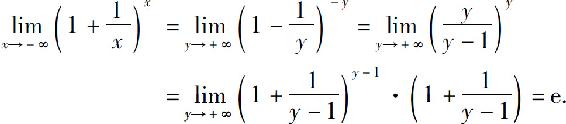
综合有
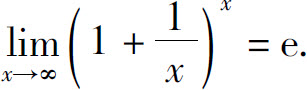
这个重要极限的另一种形式为
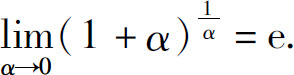
事实上,令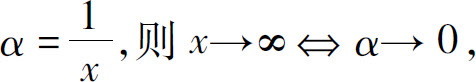 所以
所以
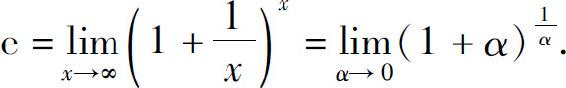
例7 计算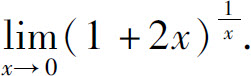
解 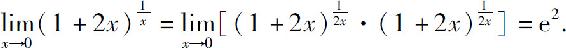
例8 计算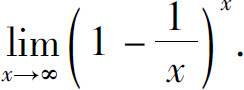
解
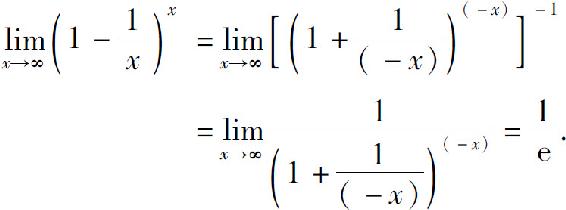
例9 设某人以本金p元进行一项投资,投资的年利率为r.如果以年为单位计算复利(即每年计息一次,并把利息加入下年的本金,重复计息),那么t年后,资金总额将变为
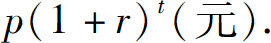
而若以月为单位计算复利(即每月计息一次,并把利息加入下月的本金,重复计息),那么t年后,资金总额将变为
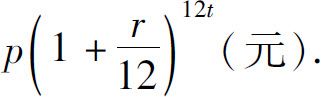
这样类推,若以天为单位计算复利,那么t年后,资金总额将变为
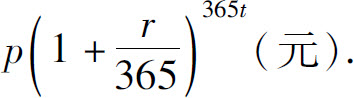
一般地,若以 年为单位计算复利,那么t年后,资金总额将变为
年为单位计算复利,那么t年后,资金总额将变为
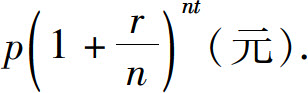
现在让n→∞,即每时每刻计算复利(称为连续复利),那么t年后,资金总额将变为
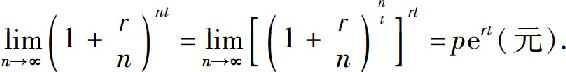
习题1.4
1.求下列极限:
(1)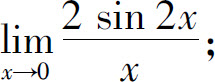
(2)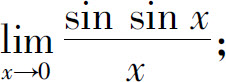
(3)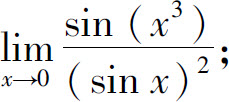
(4)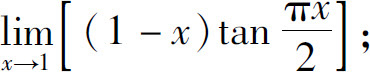
(5)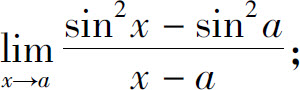
(6)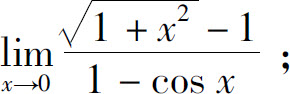
(7)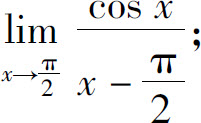
(8)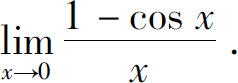
2.求下列极限:
(1)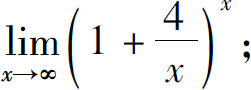
(2)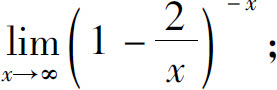
(3)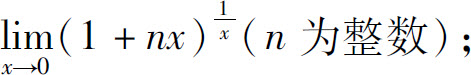
(4)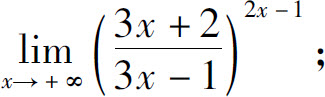
(5)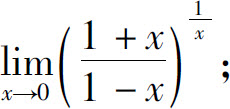
(6)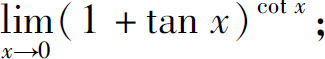
(7)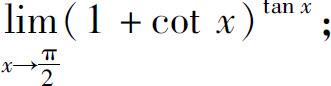
(8)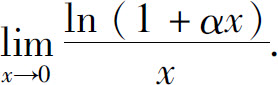
3.利用夹逼准则求下列数列的极限:
(1)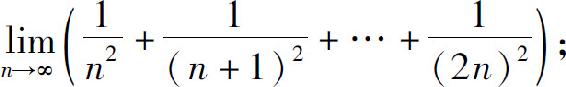
(2)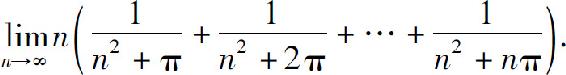
4.利用单调有界准则证明下列数列收敛.
(1)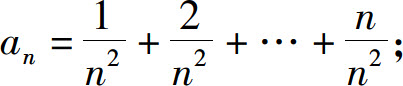
(2)