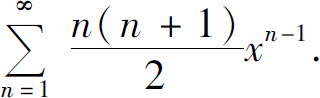8.4 幂级数
8.4 幂级数
8.4.1 函数项级数的概念
设un（x）（n＝1，2，…）是定义在区间I上的一列函数，则表达式
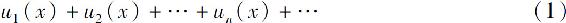
称为定义在区间I上的函数项级数．
对于区间I上的每一点x0，由函数项级数（1）可得一个数项级数
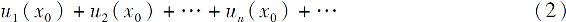
如果数项级数（2）收敛，则称点x0为函数项级数（1）的收敛点；如果数项级数（2）发散，则称点x0为函数项级数（1）的发散点．收敛点的全体称为函数项级数（1）的收敛域．
对应于收敛域内的任意一点x，函数项级数成为一个收敛的数项级数，因而有一确定的和s．这样，在收敛域上，函数项级数的和是x的函数，称为函数项级数的和函数，记为s（x），即
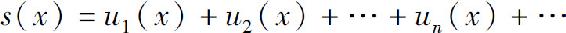
函数项级数（1）的前n项的部分和记为sn（x），则在收敛域上
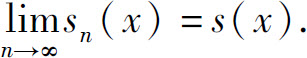
8.4.2 幂级数及其收敛半径
函数项级数中最简单而重要的一类级数就是幂级数，它的每一项都是幂函数，一般形式是
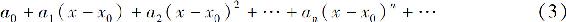
其中常数a0，a1，a2，…，an，…称为幂级数的系数．
不失一般性，我们只研究形如
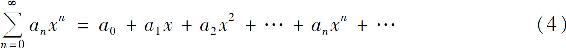
的幂级数．因为经过变换t＝x－x0，幂级数（3）就可化为（4）的形式．
现在来讨论幂级数的收敛域．
我们知道几何级数
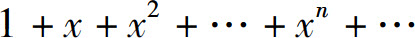
当|x|＜1时收敛，当|x|≥1时发散．因此，这个几何级数的收敛域是以x＝0为中心的开区间（－1，1）．
定理1（幂级数收敛定理） 幂级数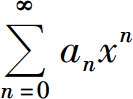
的收敛域有三种可能：
（1）存在一个正数R，使得幂级数在开区间（－R，R）内收敛，在闭区间［－R，R］外发散，在区间端点x＝±R处可能收敛也可能发散；
（2）幂级数对一切的x都收敛；
（3）幂级数只在x＝0处收敛．
这里，R称为幂级数的收敛半径，开区间（－R，R）称为幂级数的收敛区间．
如果幂级数对一切的x都收敛，则规定收敛半径R＝＋∞．如果幂级数只在x＝0处收敛，则规定收敛半径R＝0．
该定理揭示了幂级数收敛域的结构．如果R＝＋∞或R＝0，收敛半径完全决定了收敛域；而对于0＜R＜＋∞，还留下幂级数在x＝±R处的收敛性问题．
可以看出，求幂级数收敛域的关键就是找出幂级数的收敛半径．对于幂级数收敛半径R，有以下简便的求法：
定理2 给定幂级数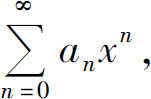
设
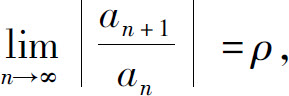
则 （1）当0＜ρ＜＋∞时，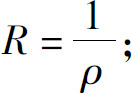
（2）当ρ＝0时，R＝＋∞；
（3）当ρ＝＋∞时，R＝0．
证 考察幂级数各项取绝对值所成的级数
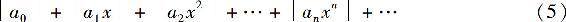
其相邻两项之比的极限
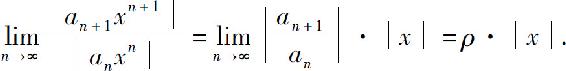
（1）如果0＜ρ＜＋∞，根据正项级数的比值判别法，当ρ·|x|＜1，即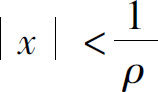
时，级数（5）收敛，从而级数
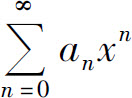绝对收敛；当ρ·|x|＞1，即
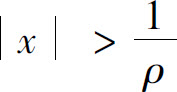时，级数（5）发散并从某个n开始
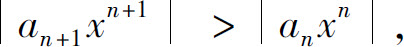因此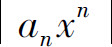
不可能趋于零，所以
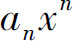也不可能趋于零，从而级数
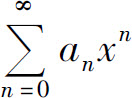发散．于是级数
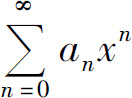的收敛半径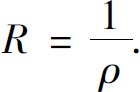
（2）如果ρ＝0，则对一切的x都有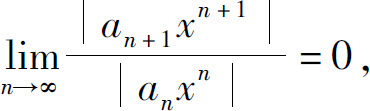
所以级数（5）收敛，从而级数
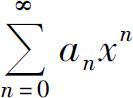收敛．于是R＝＋∞．
（3）如果ρ＝＋∞，则对任意的x≠0都有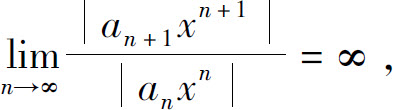
所以级数（5）发散，由（1）中同样的理由可知级数
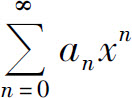发散，于是R＝0．
例1 求幂级数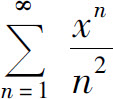
的收敛域．
解 这里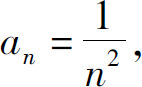
因为
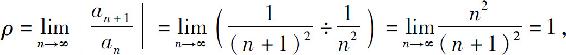
所以收敛半径R＝1，收敛区间为（－1，1）．
当x＝1时，级数成为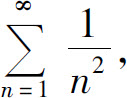
是收敛的；当x＝－1时，级数成为
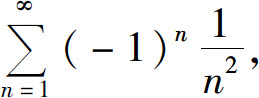也是收敛的．
综上所述，幂级数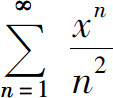
的收敛域为［－1，1］．
例2 求幂级数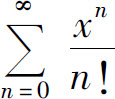
的收敛域．
解 因为
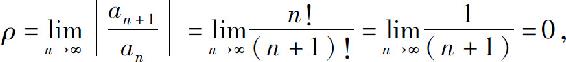
所以收敛半径R＝＋∞，收敛域为（－∞，＋∞）．
例3 求幂级数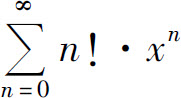
的收敛半径．
解 因为
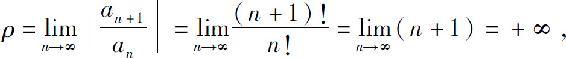
所以收敛半径R＝0，级数仅在x＝0处收敛．
例4 求幂级数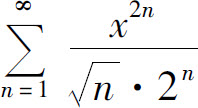
的收敛域．
解 级数缺少奇数次幂的项，定理2不能直接应用．我们用正项级数的比值判别法来求收敛半径．
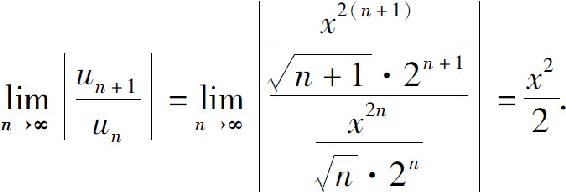
因此当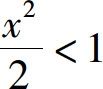
即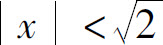
时，幂级数收敛；当
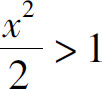即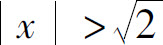
时，幂级数发散，所以幂级数的收敛半径
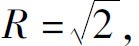，收敛区间为（
）．
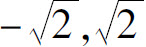当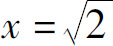
时，级数成为
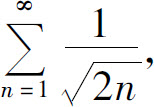是发散的；当
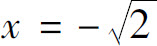时，级数成为
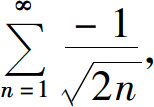也是发散的．
综上所述，幂级数的收敛域为（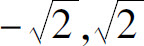
）．
最后指出，幂级数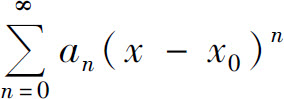
收敛域的确定，可仿照上面的方法进行讨论．
例5 求幂级数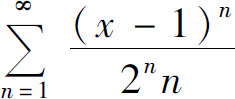
的收敛域．
解 因为
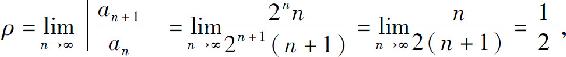
所以收敛半径R＝2，当|x－1|＜2时，级数收敛，即收敛区间为（－1，3）．
当x＝－1时，级数成为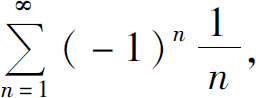
是收敛的；当x＝3时，级数成为
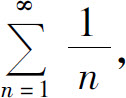是发散的．
综上所述，幂级数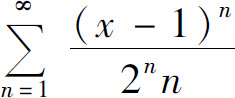
的收敛域为［－1，3）．
8.4.3 幂级数的运算
设幂级数
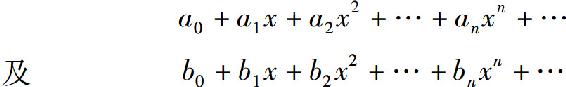
的收敛区间分别为（－R1，R1），（－R2，R2），和函数分别为s1（x），s2（x）．令R＝min{R1，R2}，则在区间（－R，R）内两级数可逐项相加、相减和相乘．
逐项相加和相减：
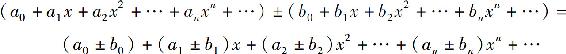
逐项相乘：
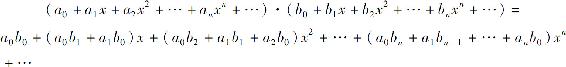
可以证明，幂级数的和函数有下列性质：
性质1 幂级数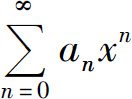
的和函数s（x）在其收敛域I上连续．
性质2 幂级数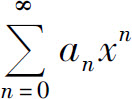
的和函数s（x）在其收敛域I上可积，并有
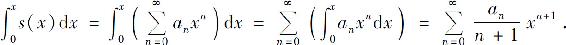
性质3 幂级数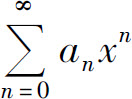
的和函数s（x）在其收敛区间（－R，R）内可导，并有
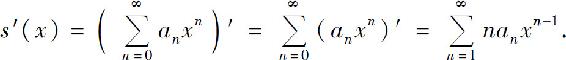
也就是幂级数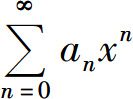
逐项积分或逐项求导后所得的幂级数与原幂级数有相同的收敛半径R，并且在区间（－R，R）内新得到的幂级数的和函数分别为原幂级数的和函数s（x）的积分或导数．
例6 求幂级数
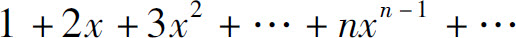
的和函数．
解 易知幂级数的收敛域为（－1，1）．设和函数为s（x），即
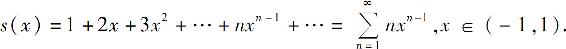
逐项积分，得
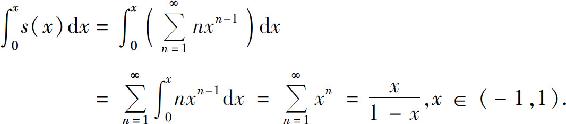
等式两边求导，得
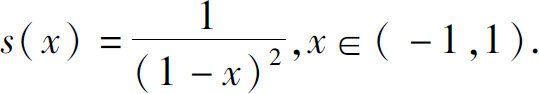
例7 求幂级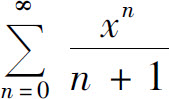数
的和函数．
解 易知幂级数的收敛域为［－1，1）．设和函数为s（x），即
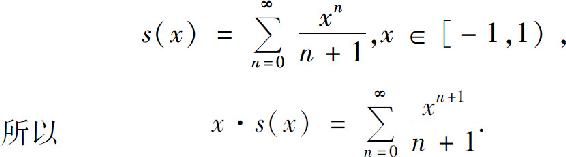
逐项求导，得
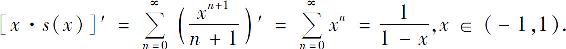
两边积分，得
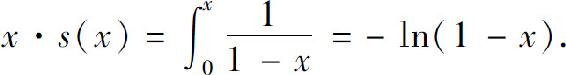
于是，当x≠0时，有
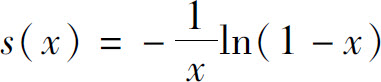
而s（0）＝1，故
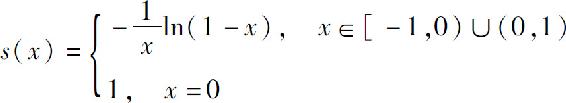
习题8.4
1．求下列幂级数的收敛域：
（1）
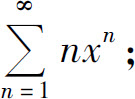
（2）
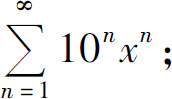
（3）
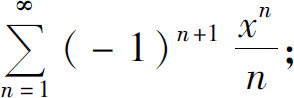
（4）
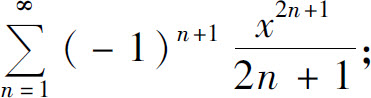
（5）
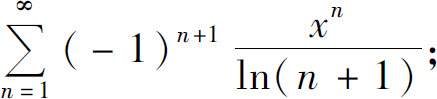
（6）
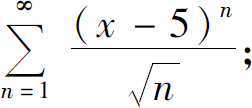
（7）
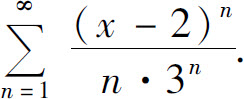
2．求下列幂级数的和函数：
（1）
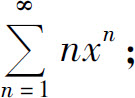
（2）