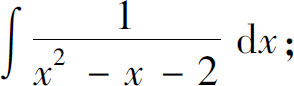习题4

习题4

一、填空题

1．函数f′（x）的不定积分是_____．

2．∫x3（1－x4）15dx＝_____．

3．若函数F（x）与G（x）是同一个连续函数的原函数，则F（x）与G（x）之间的关系式为_____．

4．设f′（ln x）＝x2（x＞1），则f（x）＝_____．

5．已知f（x）的一个原函数为cos x，g（x）的一个原函数为x2，则复合函数f［g（x）］的一个原函数为_____．

二、单项选择题

1．下列等式正确的是（　）．

A．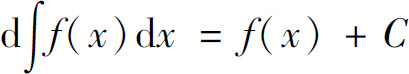
B．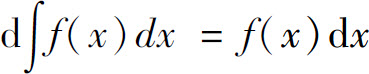
C．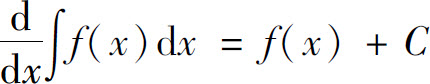
D．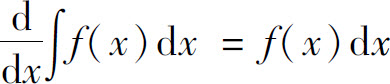

2．在区间I上，如果f′（x）＝g′（x），则一定有（　）．

A．［∫f（x）dx］′＝［∫g（x）dx］′
B．f（x）＝g（x）＋C
C．d∫f（x）dx＝d∫g（x）dx
D．f（x）＝g（x）

3．∫xf（x2）f′（x2）dx（　）．

A．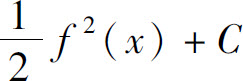
B．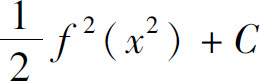
C．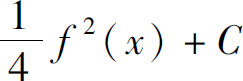
D．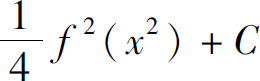

4．若∫f（x）dx＝x＋C，则∫f（1－x）dx（　）．

A．1－x＋C
B．－x＋C
C．x＋C
D．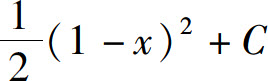

5．设f（x）连续，且∫2f（x）－1dx＝f（x）－1，则f（x）＝（　）．

A．e2x＋C
B．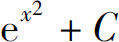
C．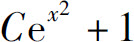
D．Ce2x＋1

三、解答题

求下列不定积分：

（1）

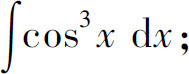
（2）

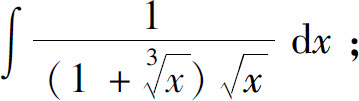
（3）

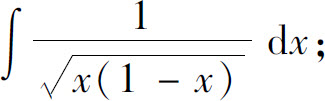
（4）

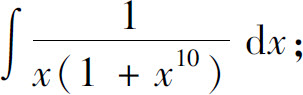
（5）

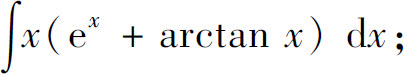
（6）

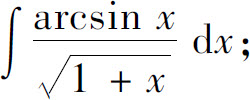
（7）