6.6 二重积分
6.6 二重积分
6.6.1 二重积分的概念
我们通过求曲边梯形的面积引入了定积分的概念,本节将从曲顶柱体的体积出发来讨论二元函数的积分学.
设函数z=f(x,y)在有界闭区域D上连续、非负,则它的图形是空间内一张连续的曲面.
现有一立体,它以曲面z=f(x,y)为顶,以区域D为底,侧面是以区域D的边界为准线而母线平行于z轴的柱面.这种立体称为曲顶柱体,如图6.13所示.
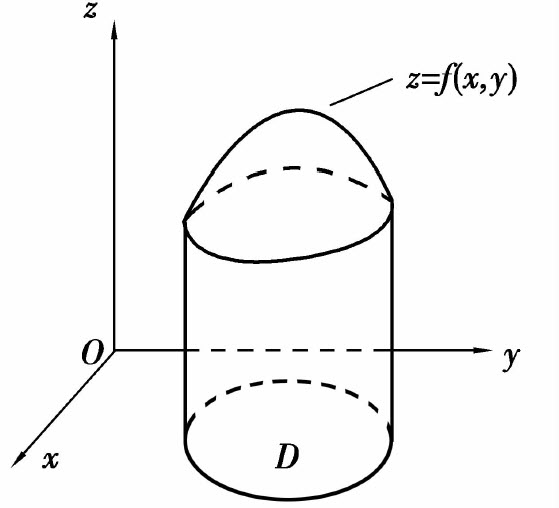
图6.13
我们采用求曲边梯形面积的方法来求曲顶柱体的体积V.
(1)分割.用曲线把区域D分割成n个小闭区域:
Δσ1,Δσ2,…,Δσn
Δσi(i=1,2,…,n)的面积仍用Δσi表示.分别以这些小闭区域的边界曲线为准线,作母线平行于z轴的柱面,这些柱面把曲顶柱体分割成n个小曲顶柱体,记第i个小曲顶柱体体积为ΔVi.
(2)近似代替.在小区域Δσi上任取一点(ξi,ηi),用高为f(ξi,ηi),底为Δσi的平顶柱体(图6.14)体积f(ξi,ηi)Δσi近似第i个小曲顶柱体体积,即
ΔVi≈f(ξi,ηi)Δσi(i=1,2,…,n).
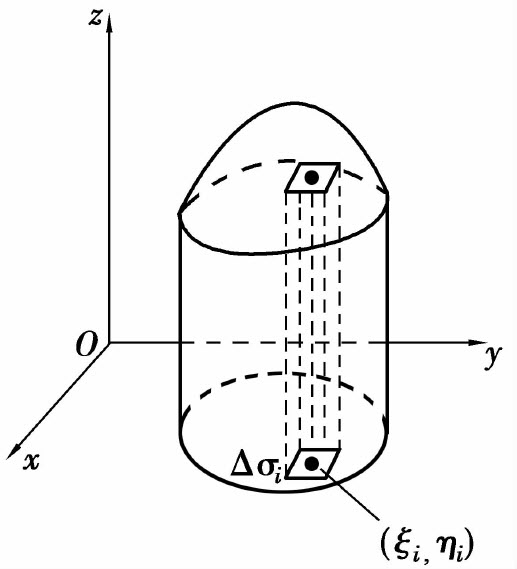
图6.14
(3)求和.这n个小平顶柱体体积之和就是曲顶柱体体积的近似值
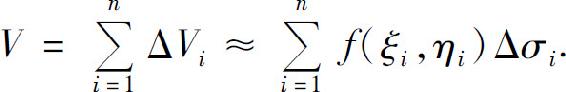
(4)取极限.用λ表示这n个小区域直径的最大值(一个闭区域的直径是指区域上任意两点间距离的最大值),当n无限增大且λ趋于0时,上述和式的极限就是曲顶柱体的体积V.即
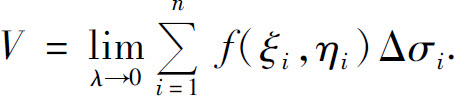
除曲顶柱体体积外,还有许多几何、物理和其他的科学技术问题都可归结为求二元函数的上述类型和式的极限.为此引入二重积分的定义.
定义 设函数z=f(x,y)在有界闭区域D上有界.将闭区域D任意分割成n个小区域
Δσ1,Δσ2,…,Δσn
并仍用Δσi表示Δσi的面积.在每个小区域Δσi上任取一点(ξi,ηi)(i=1,2,…,n),作和式
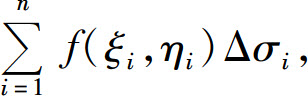
用λ表示这各小区域直径的最大值.如果λ→0时,上述和式的极限总存在,则称此极限为函数z=f(x,y)在区域D上的二重积分,记为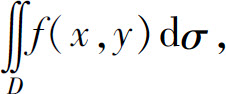 即
即
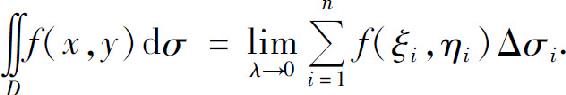
其中D称为积分区域,f(x,y)称为被积函数,f(x,y)dσ称为被积表达式,dσ称为面积元素,x与y称为积分变量.
关于二重积分的定义,作以下几点说明:
(1)二重积分只与被积函数f(x,y)及积分区域D有关.
(2)定义中对积分区域D的划分是任意的.如果在直角坐标系中用平行于坐标轴的直线网来划分D,那么除了包含边界点的一些小闭区域外(求和的极限时,这些小闭区域可以略去不计),其余的小闭区域都是矩形闭区域.设矩形闭区域Δσi的边长为Δxj和Δyk,则Δσi=Δxj·Δyk,因此在直角坐标系中,面积元素dσ也可以写作dx dy,而把二重积分记为
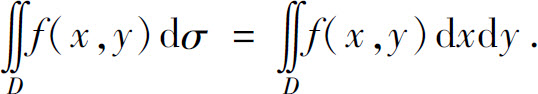
其中dσ=dx dy称为直角坐标系中的面积元素.
(3)可以证明,当被积函数f(x,y)在有界闭区域D上连续时,二重积分一定存在.
(4)二重积分的几何意义:
当f(x,y)≥0时,二重积分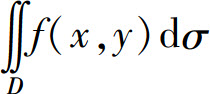 dσ就表示以积分区域D为底、以曲面z=f(x,y)为顶的曲顶柱体的体积;
dσ就表示以积分区域D为底、以曲面z=f(x,y)为顶的曲顶柱体的体积;
当f(x,y)≤0时,柱体在xOy平面的下方,故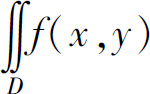 dσ表示上述曲顶柱体体积的负值;
dσ表示上述曲顶柱体体积的负值;
当f(x,y)在D上有正有负时,我们可以取xOy平面上方的柱体体积为正,xOy平面下方的柱体体积为负,那么二重积分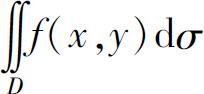 就等于这些柱体体积的代数和.
就等于这些柱体体积的代数和.
特别地,当f(x,y)≡1时,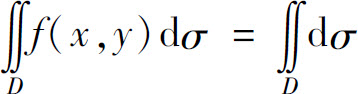 表示区域D的面积.
表示区域D的面积.
例如,上半球x2+y2+z2≤a2,z≥0的体积V可以用二重积分
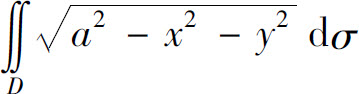
来表示,其中D={(x,y)|x2+y2≤a2}.
6.6.2 二重积分的性质
二重积分具有与定积分类似的性质,我们不加证明地叙述如下.
性质1 设α,β为常数,则
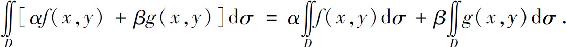
性质2 如果D被分成两个闭区域D1和D2,则
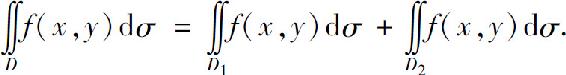
性质3 如果在D上,f(x,y)≤g(x,y),则有
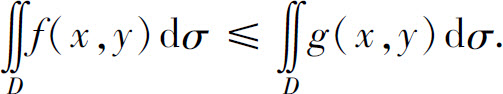
特别地,有
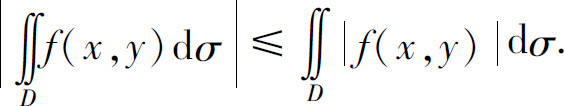
性质4 设M,m分别是f(x,y)在闭区域D上的最大值和最小值,σ是D的面积,则有
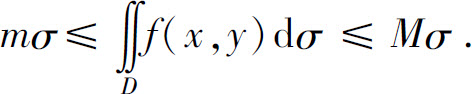
性质5(中值定理) 设函数f(x,y)在闭区域D上连续,σ是D的面积,则在D上至少存在一点(ξ,η),使得
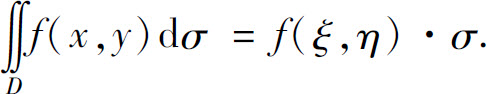
6.6.3 二重积分的计算
下面从二重积分的几何意义出发,讨论将二重积分化为两次定积分来计算的方法.
1)在直角坐标系中计算二重积分
假设f(x,y)≥0.根据二重积分的几何意义,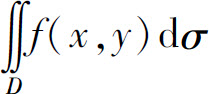 等于以区域D为底、以曲面z=f(x,y)为顶的曲顶柱体的体积V.下面用已知平行截面面积的立体体积公式来计算V.
等于以区域D为底、以曲面z=f(x,y)为顶的曲顶柱体的体积V.下面用已知平行截面面积的立体体积公式来计算V.
设积分区域D可表示为
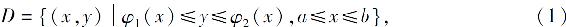
如图6.15所示,其中函数φ1(x)与φ2(x)在区间[a,b]上连续.
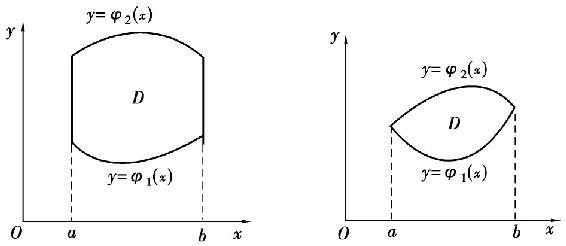
图6.15
过[a,b]上任一点x0作与yOz平面平行的平面x=x0.此平面与曲顶柱体相交所得的截面是一个以区间[φ1(x0),φ2(x0)]为底,以z=f(x0,y)为曲边的曲边梯形(图6.16的阴影部分),其面积为
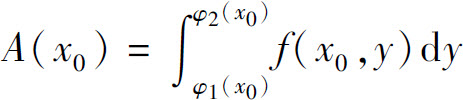
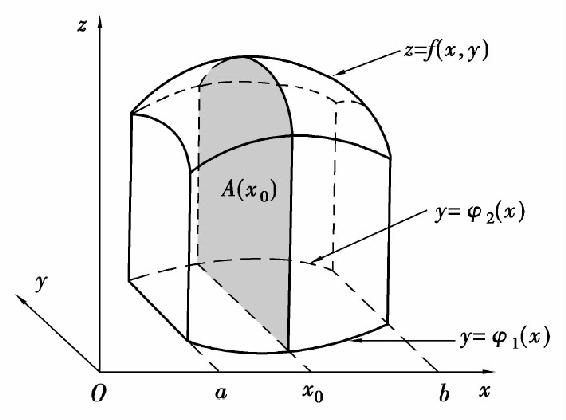
图6.16
一般地,过[a,b]上任意一点x且平行于yOz平面的平面与曲顶柱体相交所得截面的面积为
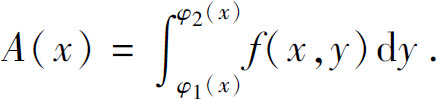
注意上式中y为积分变量,而x在积分过程中保持不变.于是
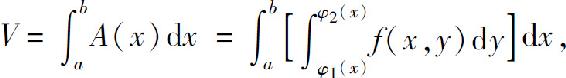
所以得二重积分的计算公式
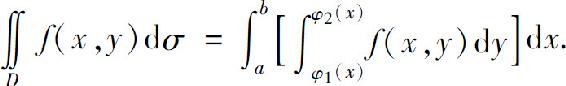
上式右端的积分叫做先对y后对x的二次积分.也就是说,先把x看作常数,把f(x,y)看作y的一元函数,并对y计算从φ1(x)到φ2(x)的定积分;然后把计算的结果(x的一元函数)对x计算从a到b的定积分.为方便起见,常写成下面的形式
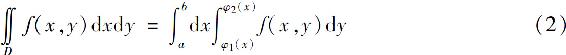
在上述讨论中,假定f(x,y)≥0,但实际上公式的成立并不受此条件限制.
类似地,如果积分区域D可表示为
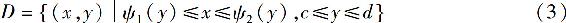
如图6.17所示,其中函数ψ1(y)与ψ2(y)在区间[c,d]上连续,则这时可以把二重积分化为先对x后对y的二次积分
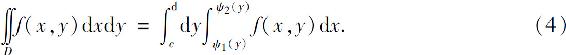
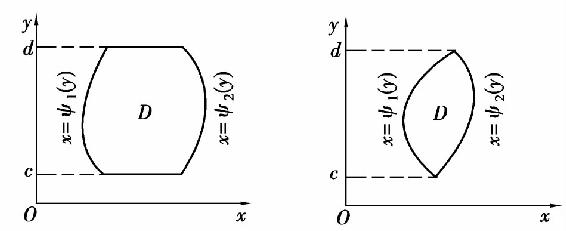
图6.17
我们称图6.15所示的区域为X型区域,图6.17所示区域为Y型区域.X型区域的特点是:穿过区域内部且平行于y轴的直线与区域边界相交不多于两个交点;Y型区域的特点为:穿过区域内部且平行于x轴的直线与区域边界相交不多于两个交点.
如果积分区域D既是X型区域,又是Y型区域,如图6.18所示.也就是说,D既可以用式(1)表示,又可以用式(3)表示,则公式(2),(4)同时成立,即
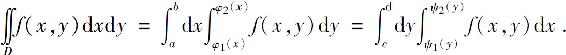
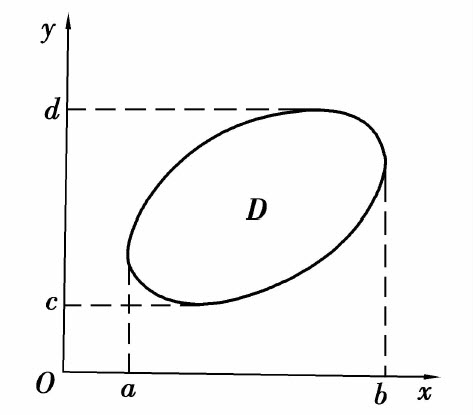
图6.18
如果积分区域D既不是X型区域,又不是Y型区域,则可以用平行于坐标轴的直线把它分成几个部分,使每个部分是X型区域或Y型区域.例如图6.19所示,把区域D分成三个部分,每个部分都是X型区域.从而每个部分区域上的二重积分都可以应用公式(2)或(4)来计算.再利用重积分的性质2,即可得到整个区域D上的二重积分.
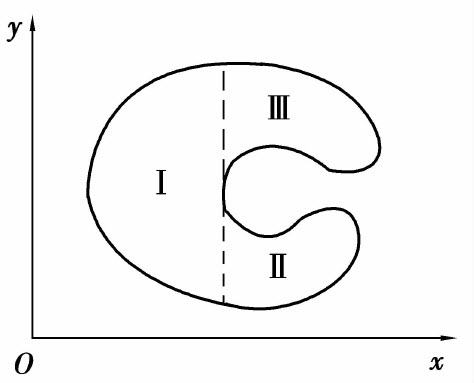
图6.19
二重积分化为二次积分的关键之一是确定积分限,而积分限是根据积分区域来确定的.假设积分区域D是X型区域,则确定积分限的步骤如下:
(1)画出积分区域D的图形;
(2)将积分区域D投影到x轴上,得到区间[a,b];
(3)在区间[a,b]上任取一点x,积分区域上以这个x值为横坐标的点在一段直线上,这段直线平行于y轴,其上点的纵坐标从φ1(x)变到φ2(x),如图6.20所示;
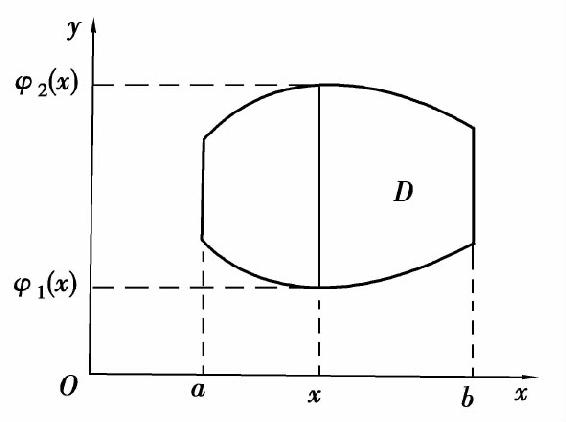
图6.20
(4)将积分区域D表示为
D={(x,y)|φ1(x)≤y≤φ2(x),a≤x≤b},
这样就得到对y积分的上、下限φ2(x),φ1(x),对x积分上、下限b,a.
值得注意的是二次积分的上限不小于下限.
例1 计算二重积分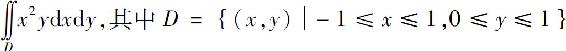 .
.
解 区域D如图6.21所示.可将二重积分化为先对y后对x的二次积分
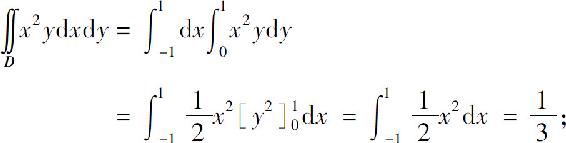
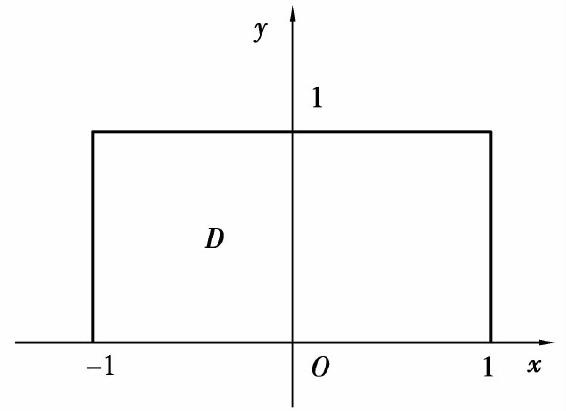
图6.21
也可将二重积分化为先对x后对y的二次积分
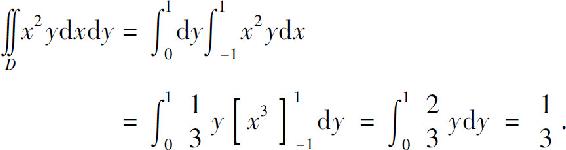
例2 设D是由直线y=x与抛物线y=x2所围成的闭区域,试求
(1)闭区域D的面积σ;
(2)求以曲面z=xy为顶、以D为底的曲顶柱体体积V.
解 区域D如图6.22所示,可以看作X型区域:

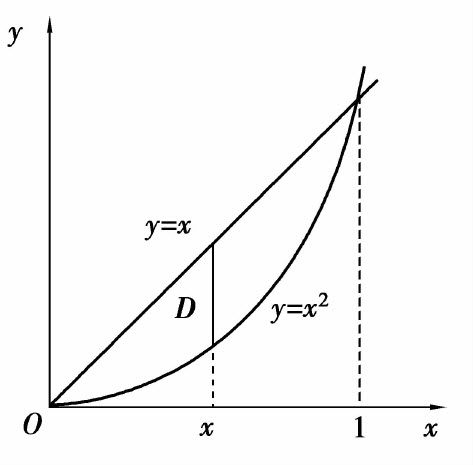
图6.22
(1)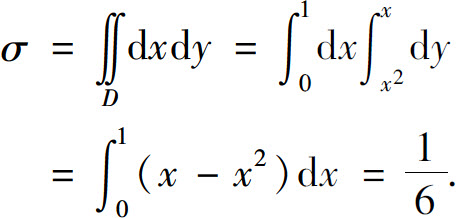
(2)由二重积分的几何意义,得
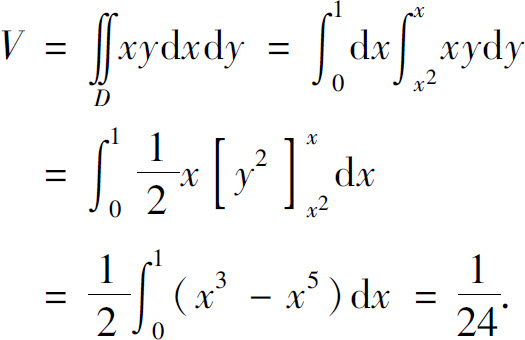
例3 计算二重积分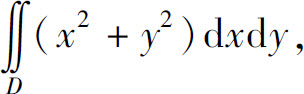 其中D是由直线y=x,y=1,y=2,y=1+x所围成的区域.
其中D是由直线y=x,y=1,y=2,y=1+x所围成的区域.
解 区域D如图6.23(a)所示,若把它看作Y型区域,可表示为
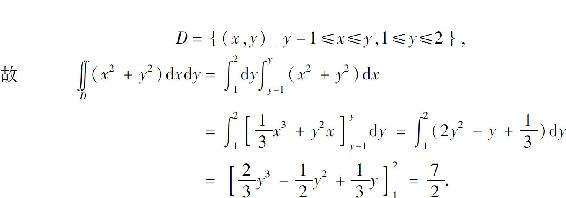
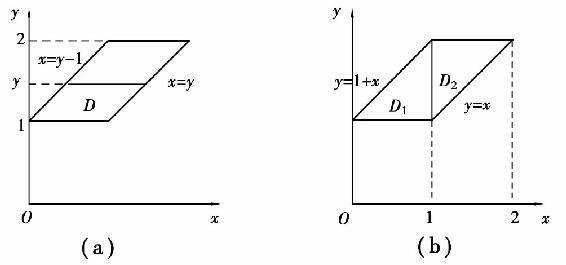
图6.23
若把区域D看作X型区域,如图6.23(b)所示,可将D分成D1和D2两个部分:
D1={(x,y)|1≤y≤1+x,0≤x≤1};
D2={(x,y)|x≤y≤2,1≤x≤2}.
于是
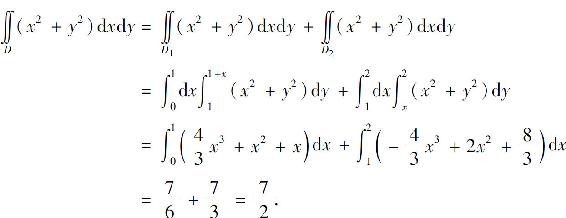
例4 计算二重积分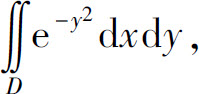 其中D是以(0,0),(1,1),(0,1)为顶点的三角形闭区域.
其中D是以(0,0),(1,1),(0,1)为顶点的三角形闭区域.
解 如图6.24所示,D可以看作Y型区域:
D={(x,y)|0≤x≤y,0≤y≤1}.
故
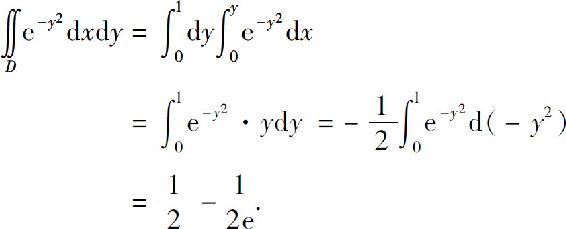
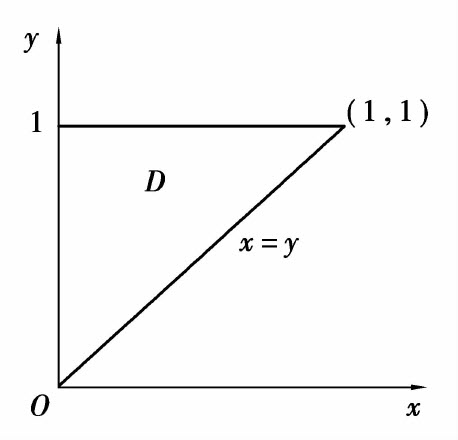
图6.24
由于被积函数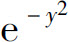 的原函数不能用初等函数表示,因此上述二重积分不宜采用先对y后对x积分的次序来计算.
的原函数不能用初等函数表示,因此上述二重积分不宜采用先对y后对x积分的次序来计算.
从例3和例4可以看出,二重积分化为二次积分时,积分次序的选择是十分关键的.如果选择的积分次序不合适,会使计算变得很复杂,甚至得不到结果.
2)在极坐标系中计算二重积分
有些二重积分,积分区域D用极坐标来表示比较简单(比如圆形、扇形),且被积函数容易用极坐标表达(比如含有x2+y2等形式),可考虑用极坐标来计算.
设函数z=f(x,y)在D上连续,由极坐标变换
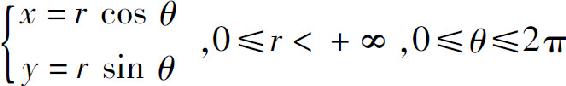
函数f(x,y)在极坐标下可以写成
f(x,y)=f(r cosθ,r sinθ).
设从极点O出发穿过区域D内部的射线与D的边界曲线相交不多于两点.由于二重积分与积分区域D的分割方式无关,我们用以极点为圆心的一组同心圆(r=常数)和一组从极点出发的射线(θ=常数)来分割区域D,如图6.25所示.这时小区域Δσ的面积
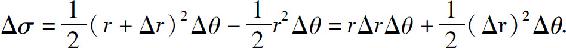
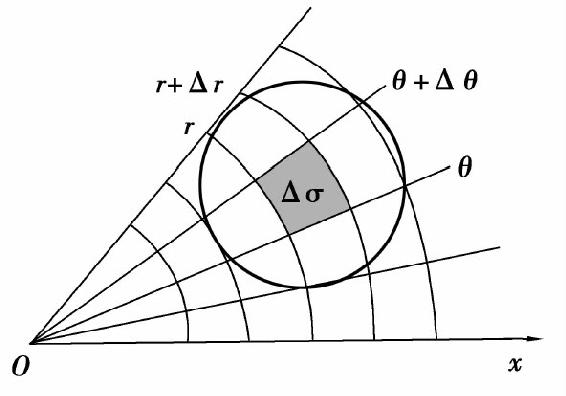
图6.25
去掉高阶无穷小,得
Δσ≈rΔrΔθ.
于是面积元素
dσ=rdrdθ.
因此
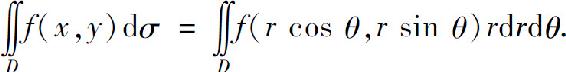
这就是二重积分的变量从直角坐标变换为极坐标的变换公式.
在极坐标系下,二重积分一般可化为先对r后对θ的二次积分,根据区域的特点分以下几种情况:
(1)极点O在区域D之外(如图6.26所示)
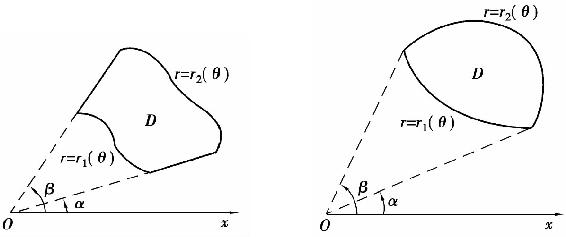
图6.26
此时区域D可表示成
D={(r,θ)|r1(θ)≤r≤r2(θ),α≤θ≤β}.
在[α,β]上任取一个θ值,对应于这个θ值,区域D上极径线段上点的r坐标从r1(θ)变到r2(θ).故
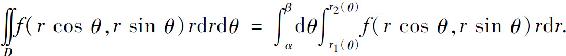
(2)极点O在区域D的内部(如图6.27所示)
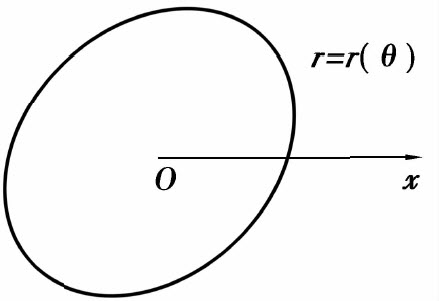
图6.27
此时区域D可表示成:
D={(r,θ)|0≤r≤r(θ),0≤θ≤2π},
故 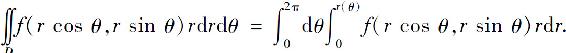
(3)极点O在区域D的边界上(如图6.28所示)此时区域D可表示成:
D={(r,θ)|0≤r≤r(θ),α≤θ≤β},
故
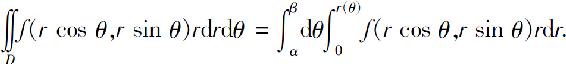
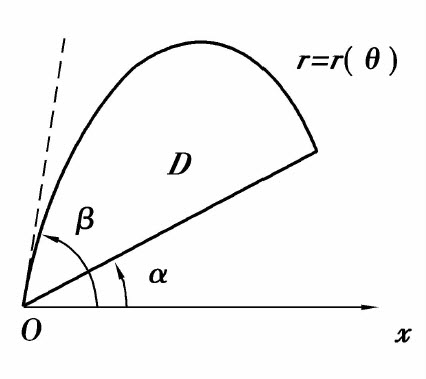
图6.28
例5 计算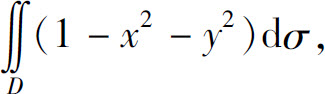 其中区域D:x2+y2≤1.
其中区域D:x2+y2≤1.
解 在极坐标系下,区域D可表示成:
{(r,θ)|0≤r≤1,0≤θ≤2π},
所以
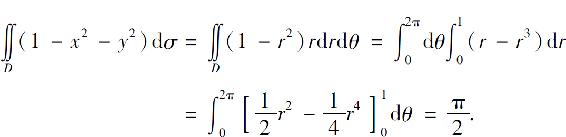
例6 计算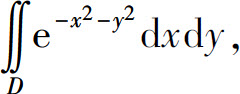 其中区域D是圆域:x2+y2≤a2在第一象限部分.
其中区域D是圆域:x2+y2≤a2在第一象限部分.
解 在极坐标系下,区域D可表示成:
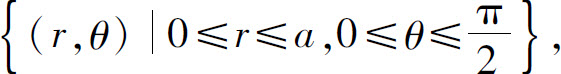
所以
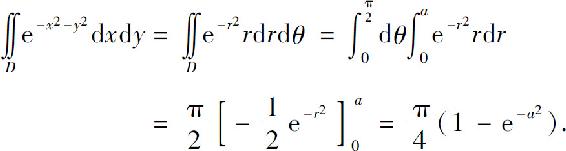
现在利用上面的结果来计算概率积分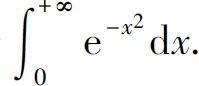 设
设
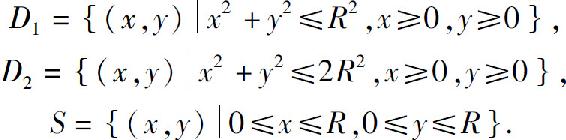
显然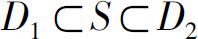 (图6.29),由于
(图6.29),由于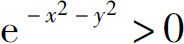 ,从而在这些闭区域的二重积分之间有如下不等式:
,从而在这些闭区域的二重积分之间有如下不等式:
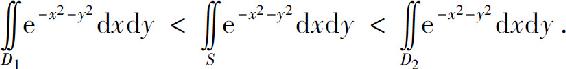
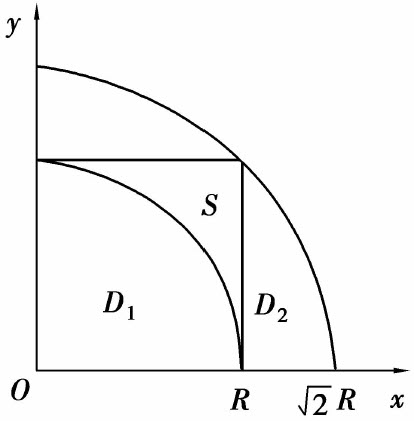
图6.29
因为
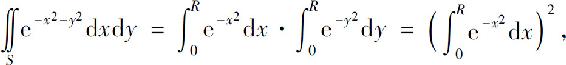
应用上面的结果,有
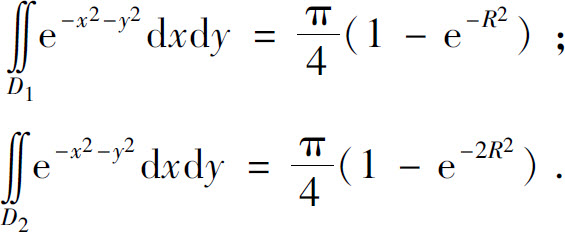
于是上面的不等式可写成
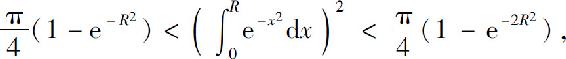
令R→+∞,上式两边趋于同一个极限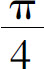 ,所以
,所以
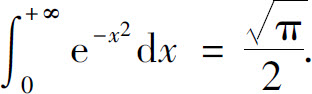
习题6.6
1.一薄板(不考虑其厚度)位于xOy平面上,占有区域D.薄板的面密度为μ=μ(x,y),试用二重积分表达该薄板的质量.
2.比较下列积分的大小:
(1)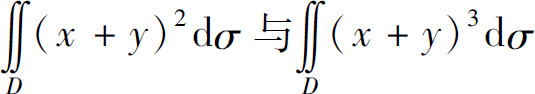 其中D是由x轴、y轴与直线x+y=1所围成的闭区域;
其中D是由x轴、y轴与直线x+y=1所围成的闭区域;
(2)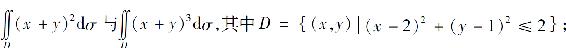
(3)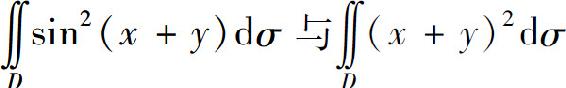 ,其中D为任一有界闭区域.
,其中D为任一有界闭区域.
3.估计下列积分的值:
(1)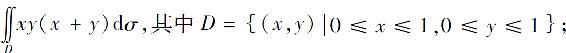
(2)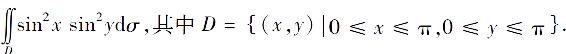
4.画出积分区域,并计算二重积分:
(1)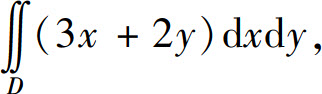 其中D为两坐标轴及直线x+y=1所围成的区域;
其中D为两坐标轴及直线x+y=1所围成的区域;
(2)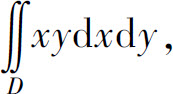 其中D为
其中D为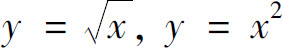 所围成的区域;
所围成的区域;
(3)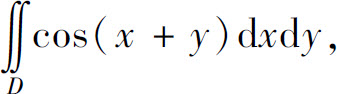 其中D为x=0,y=π,y=x所围成的区域;
其中D为x=0,y=π,y=x所围成的区域;
(4)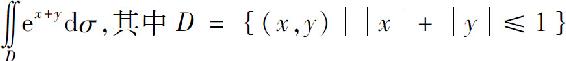 .
.
5.交换下列积分次序:
(1)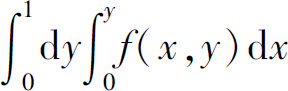 ;
;
(2)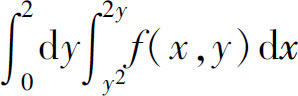 ;
;
(3)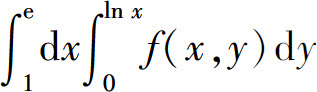 ;
;
(4)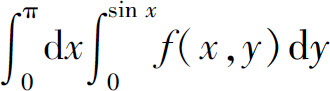 .
.
6.利用极坐标计算下列积分:
(1)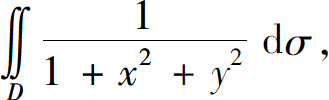 其中区域D:x2+y2≤1;
其中区域D:x2+y2≤1;
(2)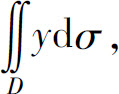 其中D为y=0,y=x和
其中D为y=0,y=x和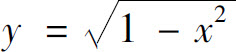 所围成的在第一象限中的区域;
所围成的在第一象限中的区域;
(3)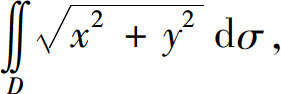 其中D是圆周x2+y2=9所围成的区域;
其中D是圆周x2+y2=9所围成的区域;
(4)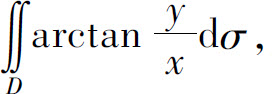 其中D是由圆周x2+y2=4,x2+y2=1以及直线y=0,y=x所围成的在第一象限中的区域.
其中D是由圆周x2+y2=4,x2+y2=1以及直线y=0,y=x所围成的在第一象限中的区域.
7.把下列积分化为极坐标形式,并计算积分值:
(1)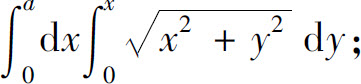
(2)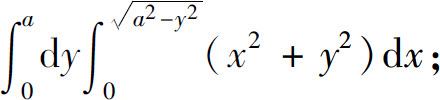
(3)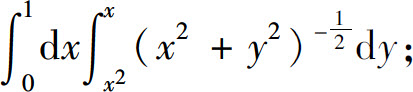
(4)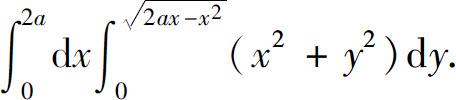
8.选用适当的坐标计算下列各题:
(1)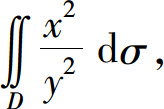 其中D是由直线x=2,y=x以及直线xy=1所围成的闭区域;
其中D是由直线x=2,y=x以及直线xy=1所围成的闭区域;
(2)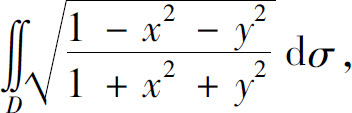 其中D是由圆周x2+y2=1及坐标轴所围成的在第一象限内的闭区域;
其中D是由圆周x2+y2=1及坐标轴所围成的在第一象限内的闭区域;
(3)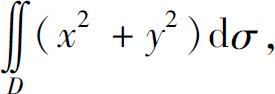 其中D是由直线y=x,y=x+a,y=a,y=3a(a>0)所围成的闭区域;
其中D是由直线y=x,y=x+a,y=a,y=3a(a>0)所围成的闭区域;
(4)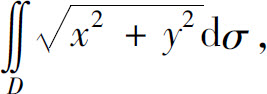 其中D是圆环形闭区域{(x,y)|a2≤x2+y2≤b2}.
其中D是圆环形闭区域{(x,y)|a2≤x2+y2≤b2}.
9.求以曲面z=x2+y2为顶、以D为底的曲顶柱体的体积V,其中D是由直线x=0,y=1和y=x所围成的区域.
10.求球体x2+y2+z2≤4a2被圆柱面x2+y2=2ax(a>0)所截得的(含在圆柱面内的部分)立体的体积.
