习题8
2025年09月17日
习题8
一、填空题
1.若级数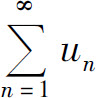 收敛,则
收敛,则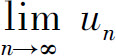 =_____.
=_____.
2.当p_____时,级数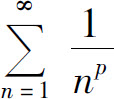 收敛.
收敛.
3.部分和数列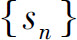 有界是正项级数钞
有界是正项级数钞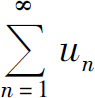 收敛的_____条件.
收敛的_____条件.
4.幂级数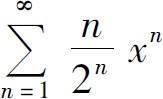 的收敛区间为_____.
的收敛区间为_____.
5.已知幂级数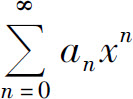 的收敛域为(-9,9],则幂级数
的收敛域为(-9,9],则幂级数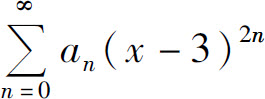 的收敛域为_____.
的收敛域为_____.
6.已知幂级数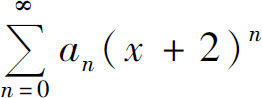 在x=0处收敛,在x=-4处发散,则幂级数
在x=0处收敛,在x=-4处发散,则幂级数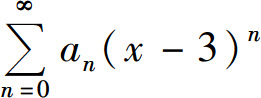 的收敛域为_____.
的收敛域为_____.
7.设幂级数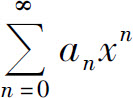 的收敛半径为3,则幂级数
的收敛半径为3,则幂级数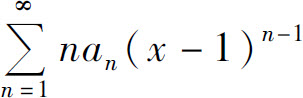 的收敛区间为_____.
的收敛区间为_____.
8.ax的麦克劳林级数为_____.
二、单项选择题
1.已知sn为级数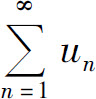 的前n项部分和,则下列命题正确的是( ).
的前n项部分和,则下列命题正确的是( ).
A.若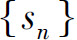 有界,则
有界,则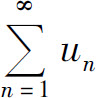 收敛
收敛
B.若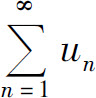 收敛,则
收敛,则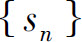 有界
有界
C.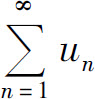 收敛的充要条件是
收敛的充要条件是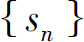 有界
有界
D.若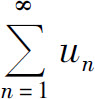 收敛,则
收敛,则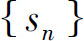 为单调有界
为单调有界
2.下面命题中,正确的是( ).
A.若级数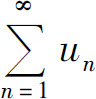 发散,则级数
发散,则级数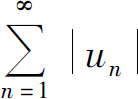 必发散
必发散
B.若级数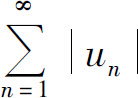 发散,则级数
发散,则级数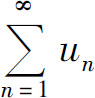 必发散
必发散
C.若级数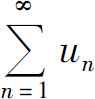 收敛,则级数
收敛,则级数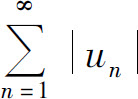 必收敛
必收敛
D.若级数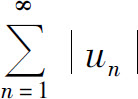 收敛,则必有
收敛,则必有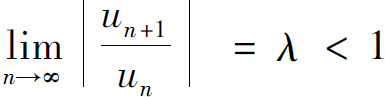
3.幂级数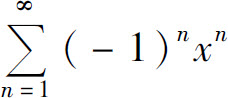 的和函数为( ).
的和函数为( ).
A.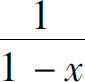
B.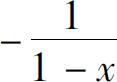
C.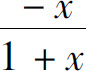
D.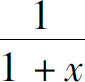
4.设级数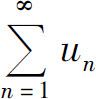 收敛,则必收敛的级数为( ).
收敛,则必收敛的级数为( ).
A.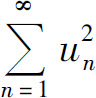
B.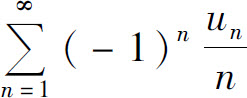
C.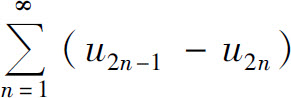
D.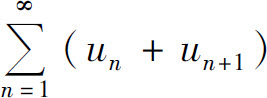
5.若级数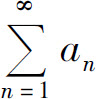 收敛,则级数( ).
收敛,则级数( ).
A.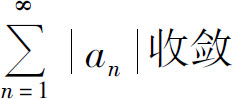
B.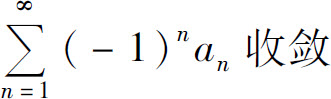
C.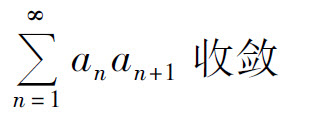
D.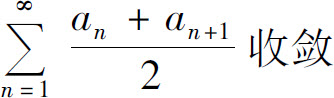
6.设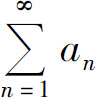 为正项级数,下列结论中正确的是( ).
为正项级数,下列结论中正确的是( ).
A.若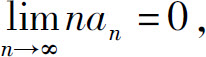 则级数
则级数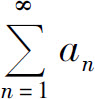 收敛
收敛
B.若存在非零常数λ,使得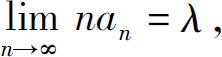 则级数
则级数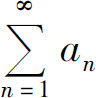 发散
发散
C.若级数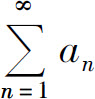 收敛,则
收敛,则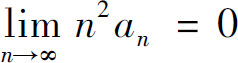
D.若级数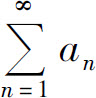 发散,则存在λ非零常数,使得
发散,则存在λ非零常数,使得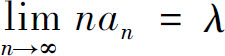
三、解答题
1.讨论级数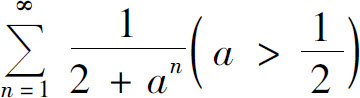 的收敛性.
的收敛性.
2.判断下列级数是否收敛?如果是收敛的,是绝对收敛还是条件收敛?
(1)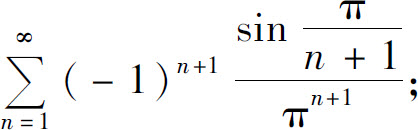
(2)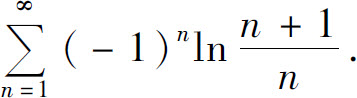
3.求幂级数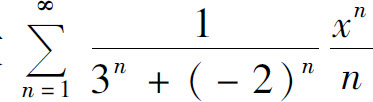 的收敛区间,并讨论该区间端点处的收敛性.
的收敛区间,并讨论该区间端点处的收敛性.
4.求幂级数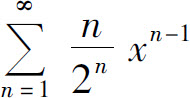 的收敛域与和函数.
的收敛域与和函数.
5.将函数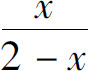 展为x的幂级数,并写出其收敛域.
展为x的幂级数,并写出其收敛域.
6.将函数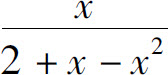 展开成x的幂级数.
展开成x的幂级数.
7.将函数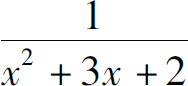 展开成(x+4)的幂级数.
展开成(x+4)的幂级数.
8.将函数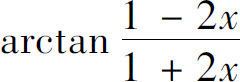 展开成x的幂级数,并求级数
展开成x的幂级数,并求级数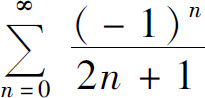 的和.
的和.
