7.2　一阶微分方程

7.2　一阶微分方程

一阶微分方程的一般形式为F（x，y，y′）＝0，如果可解出y′，则方程可写成y′＝f（x，y）的形式．本节介绍几种特殊类型的一阶微分方程及其解法．

7.2.1　可分离变量的方程

方程y′＝f（x，y）是可分离变量的，如果函数f（x，y）可以表示成一个x的函数和一个y的函数的乘积，即微分方程可写成

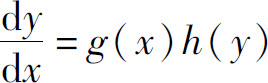
的形式．

如果h（y）≠0，则方程可化为

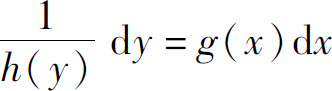
左右两边是分别只含有x和y的表达式，即已经将变量x和y分离．将方程两边积分，得

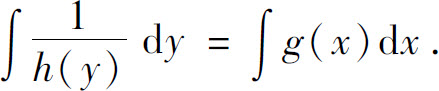
设H（y）和G（x）分别是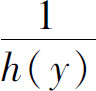和g（x）的一个原函数，则方程的通解为

H（y）＝G（x）＋C．

例1　求微分方程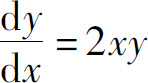的通解．

解　这是可分离变量的方程．分离变量后得

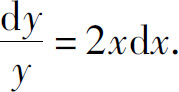
两边积分，得

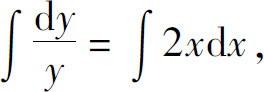
即

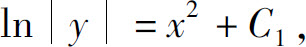
从而

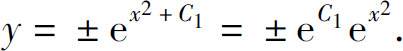
所以方程的通解

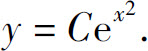
这里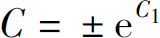，并允许C取值0，从而把解y＝0包括在内．

以后遇到类似上例的情形，可以不必写出处理绝对值的过程．

例2　求微分方程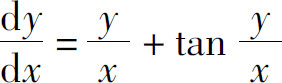的通解．

解　这个方程不能直接分离变量．作变换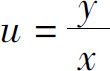，则由y＝xu得

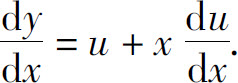
代入原方程，得

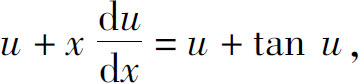
即

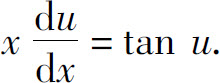
这是可分离变量方程，分离变量后得

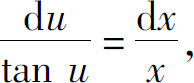
两边积分，得

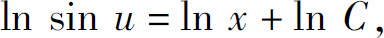
于是

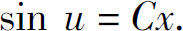
将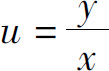代入上式，就得原方程的通解

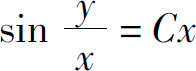
或

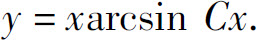
一般地，如果一阶微分方程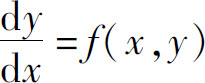可写成

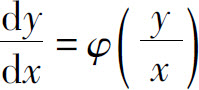
的形式，则称这方程为齐次方程．对于齐次方程，通过变量代换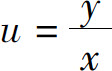可化为可分离变量的方程求解．

7.2.2　一阶线性微分方程

形如

的方程称为一阶线性微分方程，因为它是关于未知函数y及其导数的一次方程．当Q（x）恒等于零时，方程（1）成为

称为方程（1）所对应的齐次线性方程．当Q（x）不恒等于零时，方程（1）称为一阶非齐次线性方程，Q（x）称为方程（1）的自由项或非齐次项．

一阶齐次线性方程（2）实际上是可分离变量方程，分离变量后得

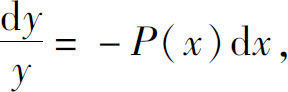
两边积分，得

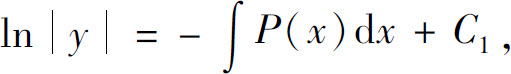
于是一阶齐次线性方程（2）的通解为

这里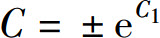，记号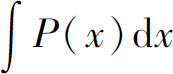表示P（x）某个确定的原函数．

现在来求非齐次方程（1）的通解．试设方程（1）的解的形式为

其中C（x）为待定函数．为了确定函数C（x），把式（4）代入方程（1）．因为

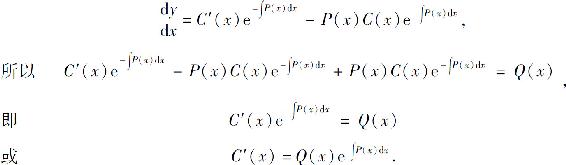
两边积分，得

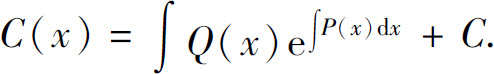
把上式代入式（4），得非齐次线性方程（1）的通解

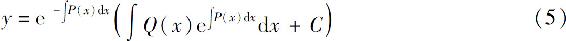
式（5）可改写为

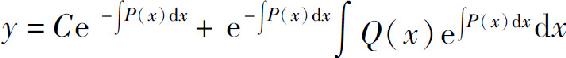
可以看出，上式右边第一项恰是相应的齐次线性方程（2）的通解，而第二项是非齐次线性方程（1）的一个特解．因此，一阶非齐次线性方程的通解等于它的一个特解与相应的齐次线性方程的通解之和．

从上面的求解过程可以看到，一阶非齐次线性方程（1）的通解可以通过把相应的齐次线性方程的通解中的任意常数换成x的函数C（x）得到，这种方法称为常数变易法．

例3　求一阶非齐次线性微分方程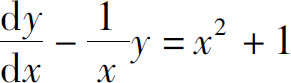的通解．

解　可用常数变易法求解．先求相应的齐次方程的通解．

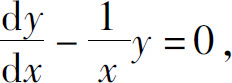
分离变量，得

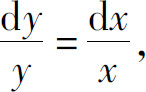
两边积分，得

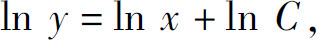
即

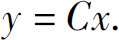
把C换成C（x），即设

则

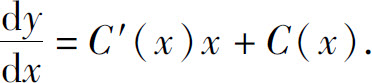
代入所给非齐次方程，得

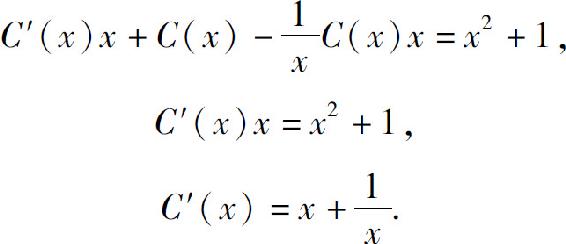
两边积分，得

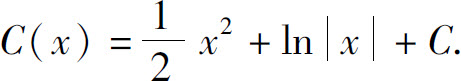
代入式（6），即得所求方程的通解

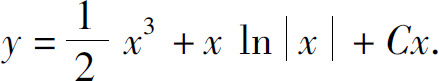
这个通解也可直接由公式（5）求得．此时

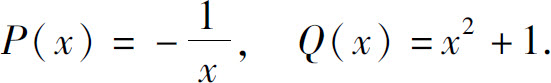
代入公式（5），得

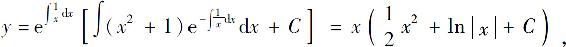
即

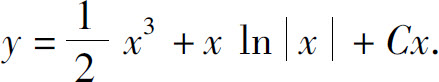
我们再来分析一下求解一阶非齐次线性方程的过程．对于一阶非齐次线性方程

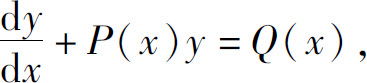
通过解相应的齐次线性方程找到变量代换

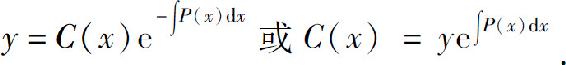
把非齐次线性方程化为变量可分离方程，然后经积分求得通解．

同样地，在前面求解齐次方程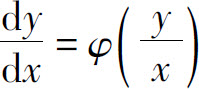时，我们也是通过变量代换y＝xu把它化为变量可分离方程，然后经积分求得通解．

利用变量代换把一个微分方程化为可分离变量方程，或化为求解方法已知的方程，是解微分方程最常用的方法之一．

例4　求方程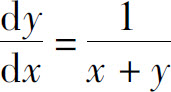的通解．

解　方程可变形为

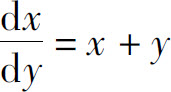
为一阶线性方程，可按一阶线性方程的解法求解．

现用变量代换来解所给方程：

令x＋y＝u，则y＝u－x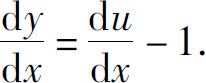，代入原方程，得

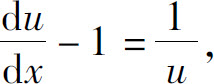
分离变量，得

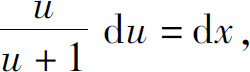
两边积分，得

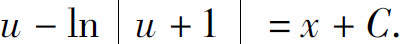
代入u＝x＋y，得到方程的通解

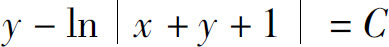
或

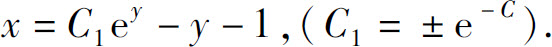
7.2.3　一阶微分方程应用举例

指数变化率　假定量y（人口、放射性元素、货币等）以正比于当前量的速率增加或减少，并知道时刻t＝0的量y0，则可以通过解下列初值问题求y．

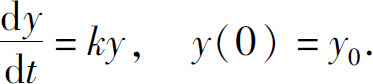
其中当y增加时，k＞0；当y减少时，k＜0．

显然，常量函数y＝0是微分方程的解．为求非零解，我们分离变量

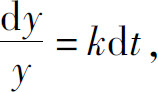
两边积分，得

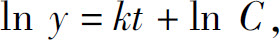
即

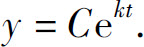
由初始条件y（0）＝y0得C＝y0，于是初值问题的解为

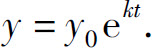
1）连续复利

假定以固定的年利率r投资p0元，一年内k次把利息加入账目，则t年后账目资金总额为

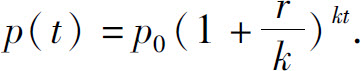
利息可以每月（k＝12）、每周（k＝52）、每日（k＝365）甚至更频繁的每小时、每分钟加入．

如果不是离散的，而是连续地以正比于账户现金的速率把利息加入账目，则由指数变化率可知t年后账目资金总额为

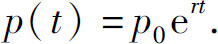
按这个公式支付的利息称为连续复利．

例5　假如你在一个账户以6.3％的年利息存款800元，8年后你将有多少钱？如果利息是：

（1）连续复利息；

（2）年度复利息．

解　这里p0＝800，r＝0.063.8年后账户中的金额是：

（1）p（8）＝800e0.063×8＝1324.26元；

（2）p（8）＝800（1＋0.063）8＝1304.24元．

2）放射性

当一个原子在放射中失去一些质量时，原子的剩余部分就重组为某种新元素的原子．这个放射过程和变化称为放射性衰减，其原子自然经过这一过程的元素，则是放射性元素．

实验指出：在任何给定的时间，放射性元素衰减的速率（单位时间改变的原子核数目）近似正比于现存放射性原子核的数目．于是放射性元素的衰减用方程

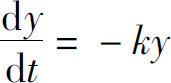
描述．这里k＞0为常数，称为衰减常数，等式右边的负号表示y是减少的．如果时刻t＝0存有放射性原子核数目为y0，则在此后时刻t仍存有的数目是

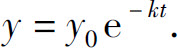
必须指出的是，衰减方程为y＝y0e－kt的放射性物质的半衰期（原子核衰减一半需要的时间）仅依赖于衰减常数k．事实上，令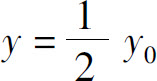，有

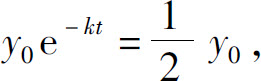
解之得半衰期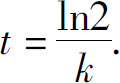

例6　利用碳－14测定年代．科学家用5700年作为它的半衰期．假设样本中原有的10％的放射性原子核已经衰减，求样本的年龄．

解　因为半衰期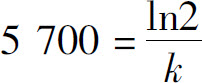，故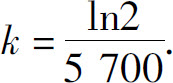需要求t的值，它满足

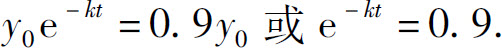
两端取对数，得

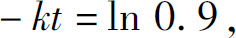
所以

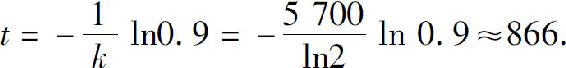
样本的年龄大约为866年．

3）混合问题

含有某种化学品的液体（或气体）流入容器中，容器中原已装有一定量的含有该化学品的液体．把混合物搅拌均匀并以一个已知的速度流出容器．

设V（t）表示在时刻t容器中液体的总量，而y（t）是在时刻t容器中的化学品总量，则在时间间隔［t，t＋dt］容器中

化学品的改变量＝化学品流入量－化学品流出量，

故

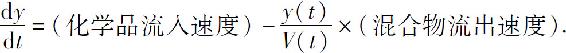
例7　某湖泊的水量为V，每年排入湖泊内含污染物A的污水量为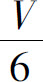，流入湖泊内不含A的水量为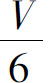，流出湖泊的水量为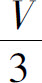．已知1999年底湖中的A的含量为5m0，超过国家规定标准．为了治理污染，从2000年初起，限定排入湖泊中含A污水的浓度不超过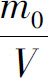．问至多需经过多少年，湖泊中污染物A的含量降至m0以内（注：设湖水中A的浓度是均匀的）？

解　设从2000年初（令此时t＝0）开始，第t年湖泊中污染物A的总量为m，浓度为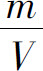，则在时间间隔［t，t＋dt］内：

排入湖泊中A的量为

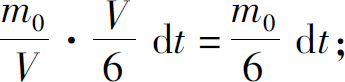
流出湖泊的水中A的量为

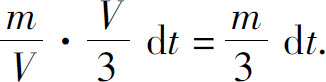
因此在此时间间隔内湖泊中污染物A的改变量为

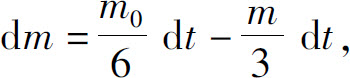
分离变量后积分，得

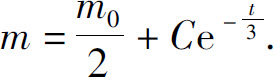
再由初始条件m（0）＝5m0得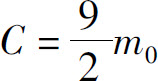，因此

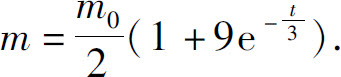
令m＝m0，得t＝6 ln 3．即至多经过6 ln 3年，湖泊中污染物A的含量降至m0以内．

习题7.2

1．求解下列微分方程：

（1）

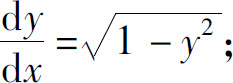
（2）

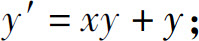
（3）

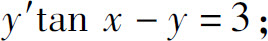
（4）

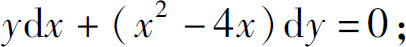
（5）

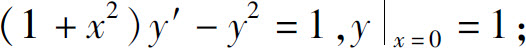
（6）

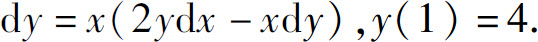
2．求解下列微分方程：

（1）

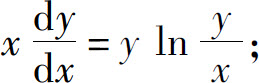
（2）

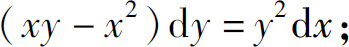
（3）

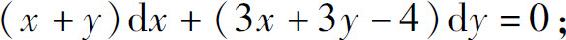
（4）

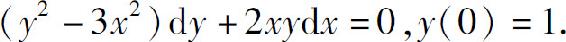
3．求下列线性微分方程的通解：

（1）

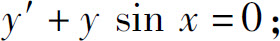
（2）

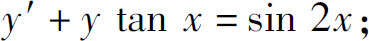
（3）

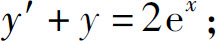
（4）

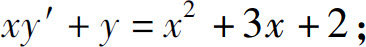
（5）

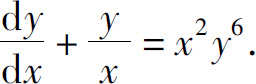
4．设曲线在其上任意一点P（x，y）处的切线斜率为2x＋y，且曲线通过坐标原点，求曲线方程．

5．一池内原有100L盐水，其中含有10kg盐，现以匀速每分钟注入2L清水，又流出2L盐水，求时刻t池内的含盐量．