2.5.2 色立体
2.5.2.1 色立体的结构
色立体是将色相、纯度、明度借助三维空间来表示的色彩系统,非常直观,易于理解。如果我们把地球仪作为模型,所有色彩的关系就可以用这样的位置和结构来类比:赤道部分表示纯色相环。南北两极连成的中心轴为无彩色系的明度序列,南极为黑,用S 表示;北极为白,用N 表示;球心为正灰。南半球为深色系,北半球为明色系。球的表面为清色系。球内为含灰色系(浊色系)。球表面任何一个到球中心轴的垂直线上,表示纯度序列;与中心轴垂直的圆周直径的两端表示补色关系。如图2.52 所示。

图2.52 借助三维空间来表示色彩系统
根据以上类比,人们得出了色立体的基本骨架(见图2.53)。它包括以下几个关键结构。
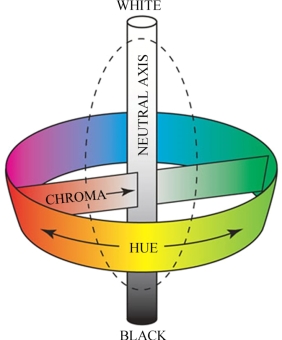
图2.53 色立体的结构
(1)明度色阶表。明度色阶表位于色立体的中心位置,是色立体的垂直中轴,分别以白色和黑色为最高明度和最低明度的极点,在黑白之间依秩序划分出从亮到暗的过渡色阶,每一色阶表示一个明度等级。
(2)色相环。色相环是以明度色阶表为中心,通过偏角环状运动来表示色相的完整体系和秩序变化。色相环由纯色组成。
(3)纯度色阶表。纯度色阶表呈水平直线形式,与明度色阶表构成直角关系,每一色相都有自己的纯度色阶表,表示该色相的纯度变化。以该色最饱和色为一极端,向中心轴靠近,含灰量不断加大,纯度逐渐降低,到达另一个极端,即明度色阶上的灰色。
(4)等色相面。在色立体中,每一个色相由于都具有横向的纯度变化和纵向的明度变化,因此构成了该色相的两度空间的平面表示。该色相的饱和色依明度层次不断向上运动靠近白色,向下运动靠近黑色,向内运动靠近灰色,这样的关系构成了该色的等色相面。如果以明度垂直轴为中心,将各色相面做放射状安排,就形成三度空间的色立体。反之,沿色立体的中心轴纵向剖开就可以得到互补色相面。
(5)等明度面。如果沿着与明度色阶表成垂直关系的方向水平地切开色立体,就可以获得一个等明度面,可以从明度色阶表的任何一个高度水平截取等明度面,不同明度面之间的对比会令我们见到色彩调性的变化。
如此一来,所有的色彩按照三要素关系就恰好填满了整个球体。事实上,光谱中各个纯色的明度是有差别的(见图2.54),如果以这样的明度序列表将球包裹起来的话,纯度最大的黄色应该不在赤道上,而是偏向N,其次为青色。纯度最大的紫色也不在赤道上,而是偏向S,这实际上是一个波浪起伏的不规则球体。
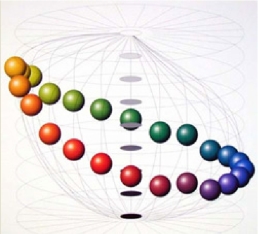
图2.54 色相环上各纯色的明度高低
此外,光谱色系中各个纯色的纯度也各不相同,如图2.55 所示。根据这一点,球模型的赤道应该是由半径各不相同的点构成的,并非圆形。因此,如果要用立体结构表达所有色彩的关系,必须在球形结构上做出一定的调整。
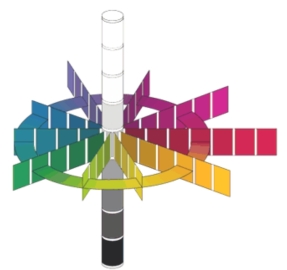
图2.55 色相环上各纯色的纯度高低
2.5.2.2 色立体的用途
(1)色立体就像一本“配色字典”。色立体为人们提供了几乎全部色彩的体系,可以帮助人们开拓思路,更方便地选择色彩。
(2)各种色彩在色立体中是按一定秩序排列的,可以指示色彩的分类、对比、调和等规律。
(3)如果建立一个标准化的色立体谱,将给色彩的使用和管理带来很大的方便。只要知道某种色的标号,就可在色谱中迅速而正确地找到它。但是,色谱也具有若干不可避免的缺点。首先,色谱只能用自己的色料制作,但色料不仅受生产技术的限制,而且在理论上受到的限制也很大。据色彩学家分析,还不可能用现有的色料印刷出所有的颜色来。其次,印刷的颜色也不可能长期保持不变色。因此在实用设计中,色立体常常作为配色的工具,辅助人们创意构思。
下面对目前世界上广泛采用的两种色立体进行介绍。
1)孟塞尔色立体
孟塞尔是美国的色彩学家,长期从事美术教育工作。孟氏色谱是从心理学的角度,根据颜色的视知觉特点所制定的标色系统,目前国际上普遍采用该标色系统作为颜色的分类和标定办法。
孟氏色立体的色相环主要有10 个色相组成:以红(R)、黄(Y)、绿(G)、蓝(B)、紫(P)为5 个基本色,在相邻的色相间各增加黄红(YR)、绿黄(GY)、蓝绿(BG)、紫蓝(PB)、红紫(RP),构成10 个主要色相。每个色相又详细地分为10 个等分,于是总共展开为100 个色相。色相名用序号表示,如1Y,2Y,…,5Y,10Y,其中5Y 为该色的代表色黄色。如图2.56 所示。
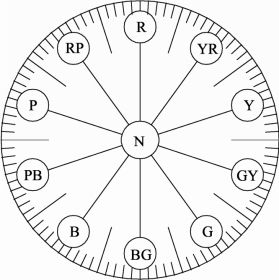
图2.56 孟塞尔色相环
中心轴是无彩色系的黑、白、灰序列,分为11 个明暗等级,黑色为0 级,白色为10 级,中间1~9 级为灰色。同时,中心轴也是有彩色系的明度标尺,其他色相的明度与中心轴的明度相对应,所有色相的位置也随其自身明度的高低变化而变化。例如,黄色的最纯色相明度值是8,而紫色的最纯色相的明度值仅为4。
色立体的纯度序列与中心轴相垂直,呈水平分布。色立体最外层是最饱和的色相,中心轴的纯度为0。越靠近外层纯度越高,越接近中心轴则越灰。由于各饱和色的纯度等级不同,所以它们的位置与中心轴的距离显得参差不齐。如蓝绿色距离中心轴最近,而红色距离中心轴最远。如果从色立体明度值为5 处做一个横剖面就可以发现,剖面不是一个正圆形,呈现出各个色相的数值大小,纯度最高的是红色,为14;5B 的纯度为10,5G 纯度为10。
按照以上方式构造出来的孟塞尔色立体,外观凹凸不平,像一个不规则球体,如图2.57、图2.58 所示。
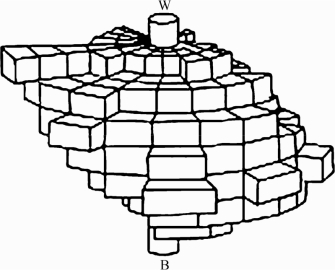
图2.57 孟塞尔色立体的外观
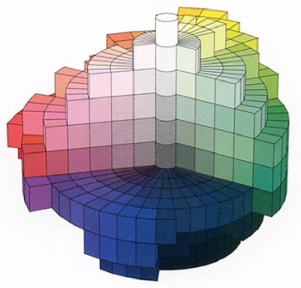
图2.58 孟塞尔色立体的剖面
在这个体系中,每个颜色都可以用色相/明度/纯度(即H/V/G)来表示,如5R/4/14表示色相为第5 号红色,明度为4,纯度为14,该色为中间明度,纯度为最高的红。
图2.59 为孟塞尔色立体俯视图,图2.60、图2.61 为孟塞尔色立体纵剖面。
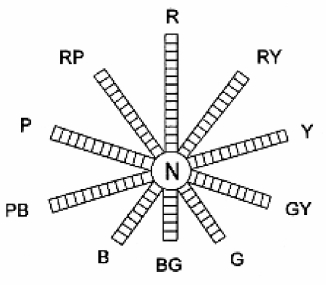
图2.59 孟塞尔色立体俯视图
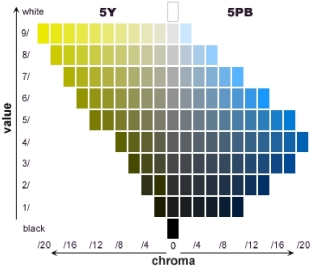
图2.60 孟塞尔色立体蓝—黄纵剖面
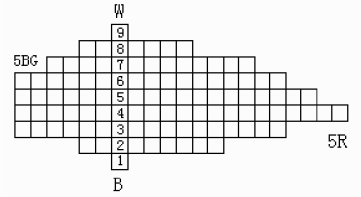
图2.61 孟塞尔色立体红—绿纵剖面
2)奥斯特瓦德色立体
奥斯特瓦德是德国化学家、诺贝尔奖获得者,他在染料化学方面作出过很大的贡献。1921 年他出版了一本《奥斯特华德色彩图示》,后被称为奥氏色立体。这个色立体的色相环以赫林的红、黄、蓝、绿四原色学说为理论依据,在临近的两色之间增加橙、蓝绿、紫、黄绿四间色,共8 个主要色。上述各色再划分为三等分,扩展成24 色相环,以1~24 来标记,每个色相均以中间的2 号为正色,色相环直径两端的色互为补色(见图2.62)。
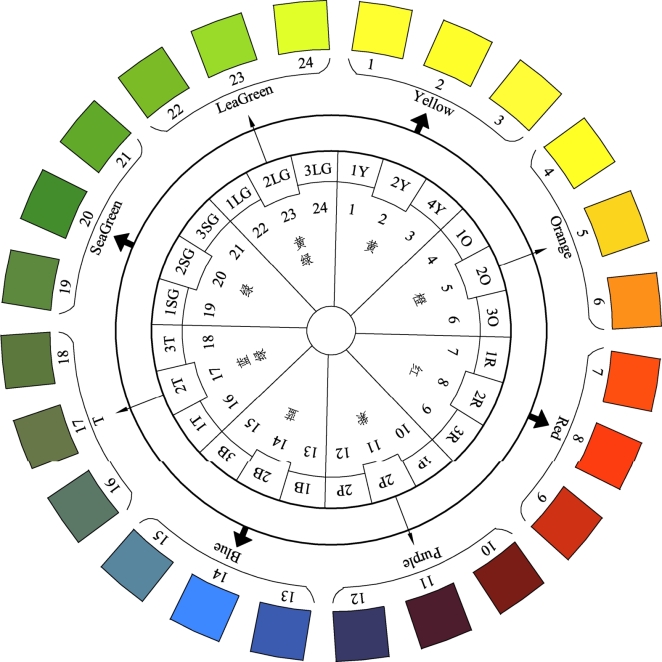
图2.62 奥斯特瓦德色相环
奥氏体系的中心轴由白至黑共计8 个明度等级,分别用a、c、e、g、i、l、n、p 表示,每个等级都具有一定的含白量和含黑量,以a 为最明亮的白色,p 为最暗的黑色,中间6 个层次为灰色。奥斯特瓦德认为,不存在真正的纯白和纯黑,所以色立体上的所有色相都被视为在纯正色相上调入不同量的白色与黑色混合而成。各个色的比例为:纯色量+白+黑=100%。每个色都以“色相号/含白量/含黑量”来标示。如8ga 表示为:8号色(红色),g 是含白量,由表查得22;a 是含黑量,查得是11,结论是浅红色。
在奥氏色立体中,以明暗系列为垂直中心轴,并以此作为三角形的一条边,其顶点为纯色,上端为明色,下端为暗色,位于三角中间部分为含灰色。若以中心轴为旋转轴,将等色相的三角形旋转360°,就构成了色相环水平放置而外形为规则的复圆锥体状的奥斯特瓦德色立体(见图2.63)。

图2.63 奥斯特瓦德色立体
