7.2　dsolve求解常微分方程

7.2　dsolve求解常微分方程

dsolve主要用来求解符号常微分方程或方程组，并给出相应的解析形式。

例1：使用dsolve求解傅科摆摆锤运动轨迹方程的通解。

从上面解析解表达式中读者很难看出摆的运动形式。为直观认识摆动过程，可以利用MATLAB命令对解析解进行可视化处理。实现可视化最重要的两个步骤是画摆绳和摆锤，并让摆绳和摆锤按上述表达式在不同的时刻出现在不同的位置。

画摆锤和摆绳可以用MATLAB的line函数实现。

例2：使用line命令，画出一条摆绳和一个摆锤。

输出结果如图7-2所示。

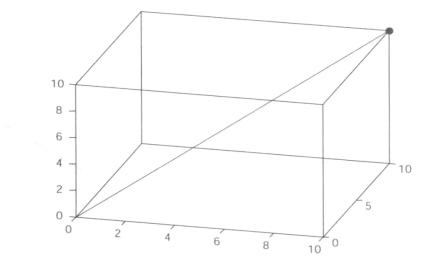
图7-2　摆锤和摆线

在新的时刻，通过set函数设置摆线和摆锤的line对象的xdata、ydata、zdata属性，可以画一条新的摆线和摆锤。这就实现了动态显示。

此外，为了更明显地显示摆平面的变化，还可以通过line函数将摆锤的轨迹记录下来，并进行实时更新。

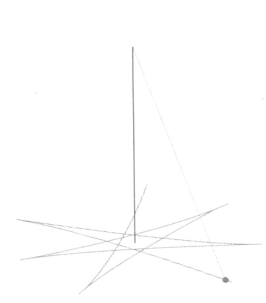
图7-3　傅科摆的运动轨迹

以真实傅科摆（摆长67 m，摆锤质量28 kg）为例，对上述解析解进行可视化显示，最终的程序列举如下。程序运行之后提示输入纬度值、x方向初始坐标x0、y方向初始坐标y0、x方向初始速度u0，以及y方向初始速度v0等参数，之后程序便显示动态的摆动效果。真实傅科摆的摆平面转动周期非常长（为32 h），为了使摆平面转动效果更明显，可在程序中增大地球自转角速度，使程序显示一种“夸大”的摆平面转动过程。

图7-3所示为纬度值为45° ，x0=2，y0=2，u0=0，v0=0，且地球自转角速度为2π/ 100时（真实角速度为2π/86 400），摆锤的运动轨迹。