10.1.2 求解步骤
以一个简单的弹性力学问题为例来说明求解步骤。如图10-2所示的平面悬臂梁模型,左端为固定端,上部受均布载荷q作用。求解x方向的正应力。
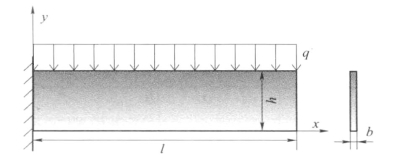
图10-2 悬臂梁模型
有限元的具体实施过程如下。
(1)单元划分
将模型划分为若干个单元。本例中选用平面四节点矩形单元,将模型划分为4个单元,并给单元和节点编号,如图10-3所示。
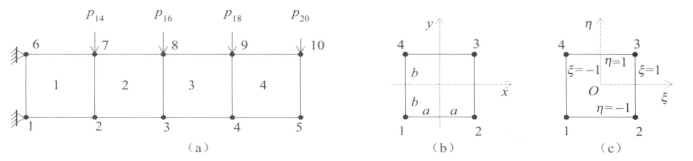
图10-3 有限元模型
(a)单元划分;(b)直角坐标系下单元示意;(c)正则坐标系下单元示意
平面四节点矩形单元的每个节点有2个自由度,因此该模型共有20个自由度。位移向量e和节点载荷向量F的维度为20 × 1,总刚度矩阵K的维度为20×20。
(2)确定位移向量和节点载荷向量
根据物理模型写出位移向量e和节点载荷向量F。对于本例,可知节点位移向量为
![]()
由于节点1和6固定,可确定e1、e2、e11、e12为0,其他自由度未知,需要求解。节点载荷向量为
![]()
其中,p1、p2、p11、p12未知。剩余的分量中,p20=aq,p14=p16=p18=2aq,其他为0。
(3)求解单元刚度矩阵ke
平面四节点矩形单元有4个节点,8个自由度,因此ke的维度为8×8。根据有限元理论可知

其中
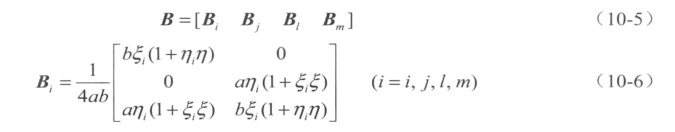
其中

为单元的局部坐标;
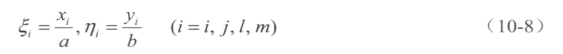
为节点i在局部坐标系的坐标值。(https://www.daowen.com)
对于平面应力问题
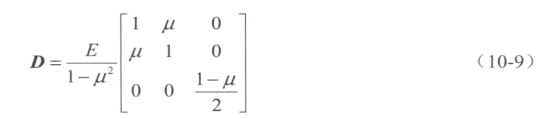
对于本例中的平面4节点单元,最终ke可表示为

其中,kij是2×2的矩阵,具体形式为
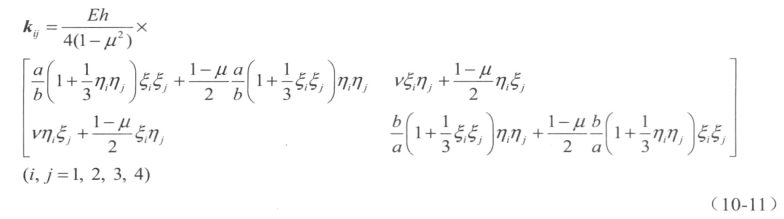
(4)组装总体刚度矩阵K
根据有限元理论,刚度矩阵中的元素表示当节点发生单位位移时引起的节点力。在单刚ke中,kij表示j节点发生单位位移且其他节点位移为零时,单元在i节点引起的节点力。类似地,在总刚K中,kij表示j节点发生单位位移且其他节点位移为零时,整体结构在i节点引起的节点力。由于结构已经被离散为若干个单元,该节点力为所有与i、j节点相关的单元在i节点引起的节点力之和。因此,总刚是由单刚按一定规则组装起来的。
根据有限元总刚组装规则,对前述问题的总刚进行计算。
已知总刚度矩阵K的维度是20 × 20,将其分成10× 10的分块矩阵,每个分块矩阵为2×2,下面所有的操作均为对分块矩阵的操作。
首先组装单元1,此时的总刚度矩阵所有元素均为0。单元1的刚度矩阵为k1。单元1中4个节点依次对应整体模型的编号是1、2、7、6(按逆时针顺序)。将k1中分块矩阵的下标1、2、3、4依次用1、2、7、6代替,并叠加到K矩阵的对应标号的分块矩阵上。单元1组装完成后,再对单元2进行组装。前两个单元组装完成后的K如图10-4所示。
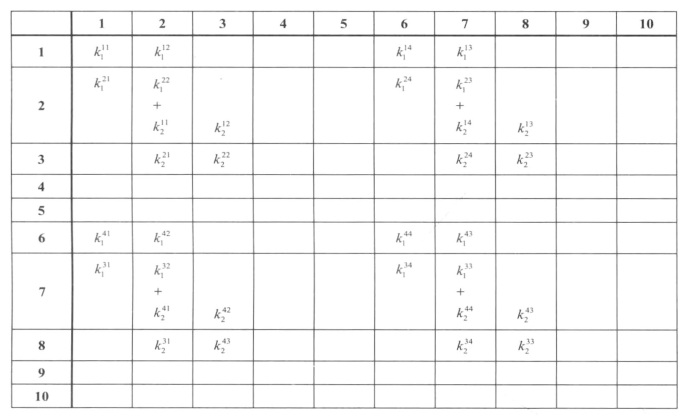
图10-4 组装了两步的总刚
依次对所有单元完成组装,得到的K如图10-5所示。
(5)求解方程
组装完成后的K不是一个满秩矩阵,若不做处理,方程(10-1)没有唯一解。因此,在求解之前,需要将已知边界条件引入,以使K满秩。对于本问题,具体做法是:将K矩阵的第1、2、9、10行和列去掉,同时将e、F向量的第1、2、9、10行去掉,组成一个新的线性方程组
![]()
进行求解。线性方程组求解可用数值分析中的各种算法完成。
(6)后处理
后处理主要包括求应力、应变及画图显示结果等。记任一单元8个自由度的位移向量为δe,则单元内任意一点的应变为

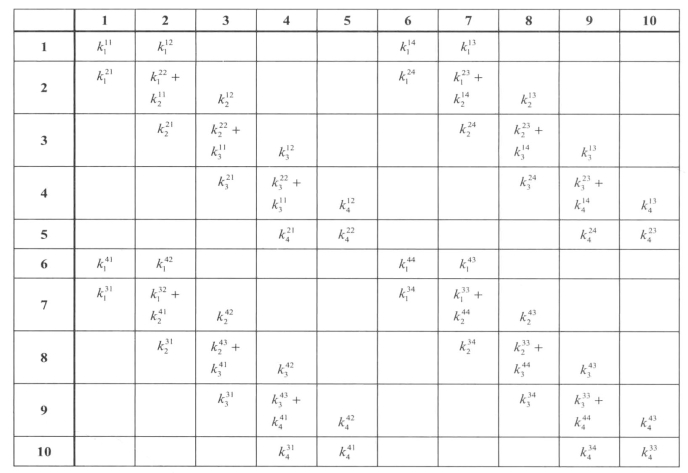
图10-5 总刚K
单元内任意一点的应力为

