8.2　用ode45求解常微分方程

8.2　用ode45求解常微分方程

上述微分方程组比较复杂，用dsolve求解解析解非常耗时，且不一定可行。在实际应用中，对于复杂的微分方程（组），很多时候解析解是很难得到的，因此经常以求解数值解来代替解析解。本节介绍一个求解微分方程数值解的函数—ode45。ode45采用四阶和五阶Runge-Kutta单步算法，用变步长求解器求解非刚性常微分方程，其解具有二阶精度。在MATLAB中，ode45是解决微分方程（组）数值解问题的首选方法。

ode45求解常微分方程（组）的最重要一步就是对方程（组）进行降阶处理，使求解方程（组）全部变为一阶微分方程。对于式（8-2），可进行如下降阶处理。

令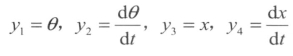,则式（8-2）化为四个一阶微分方程：

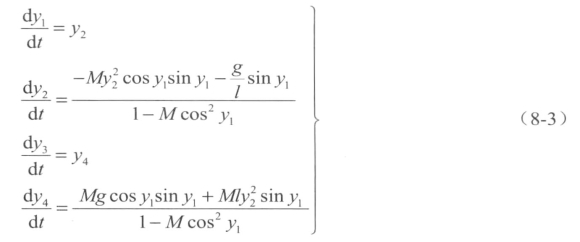
进行降阶处理后，就可用ode45命令直接求解。

为了更直观地了解滑动摆滑块与摆锤之间的相对运动，可以利用MALTAB的可视化功能对滑动摆的运动进行可视化模拟。滑动摆的可视化过程与上一章傅科摆可视化类似，这里不再赘述，只给出程序。

可视化程序完成两个功能：第一是绘制系统运动参数x和θ的时程变化曲线（图8-2），第二是生成一个模拟滑动摆运动过程的动画（avi视频文件）。图8-3是其中一帧图像（动画制作的内容将在第9章介绍）。

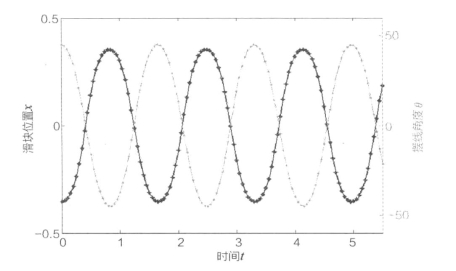
图8-2　滑块位置与摆线角度随时间变化曲线

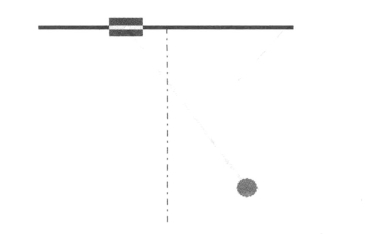
图8-3　某时刻滑动摆的运动状态图