11.4.1　复杂边界条件的设置和复杂载荷的施加

11.4.1　复杂边界条件的设置和复杂载荷的施加

从前面的实例演示不难看出，应用PDE工具箱求解平面应力问题和平面应变问题最为复杂的步骤就是给边界条件赋值，在边界条件设定好后，后面的求解就很简单了。对于力学问题的给边界条件赋值，可简单总结为：位移边界条件对应的是Dirichlet类型，力边界条件对应的是Neumann类型。

在上一节的例子中，边界条件都比较简单，因而比较容易设定。对于一些复杂的边界条件，其设定需要一些技巧。

例：如图11-24所示问题，如何在偏微分方程工具箱中设定各种边界条件和载荷？

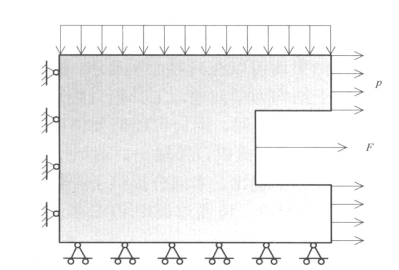
图11-24　受集中力作用的有限元模型

按照之前的总结，可知边界条件赋值方法见表11-2。但对于集中力，仍无现成方法可以采用。

表11-2　边界条件赋值方法

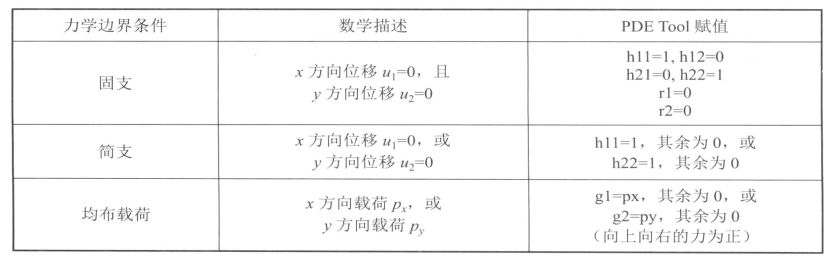
在PDE Toolbox中，虽没有施加集中力的边界条件可选，但可以用变通的手段来实现：可将集中力F均匀分散在受力点周围的一小段区域，等效为作用于l长边界上的均布力p=F/l。则图11-24可以做如图11-25 （a）所示的近似处理，图11-25 （b）中蓝色区域即为等效集中力加载边界。

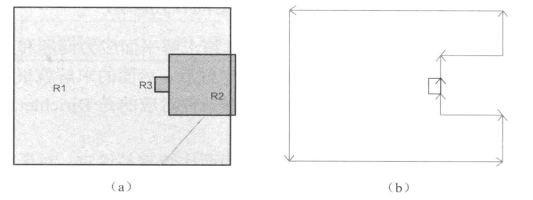
图11-25　含集中力模型的简化