11.3.2 含中心圆孔矩形板的拉伸问题
如图11-15所示，边长l=1 m的正方形薄板中心含直径为0.1 m的圆孔，板两对边受均布拉力载荷p=100 MPa，另外两对边为自由边界。弹性模量E=210 GPa，泊松比v=0.3。求圆孔周围A点和B点的应力集中系数。
圆孔周围的应力集中系数是实际应力与名义应力σ= 100 MPa的比值，因此，上述问题转化为求解正方形板在拉伸载荷作用下的应力场。
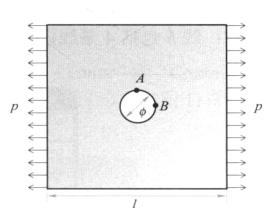
图11-15 求解模型
（1）建模
在Command Window中输入“＞＞pdetool ”，启动PDE Toolbox。单击工具栏中的
按钮，在绘图区画一个矩形R1；同理，用
按钮画一个椭圆E1。先后用鼠标左键双击矩形和椭圆，在弹出的对话框中填入图11-16中所示的数字，生成如图11-17所示的求解区域（这里也可以先设置Grid spacing，再选用Grid和Snap来定位图形，划定求解区域）。
在“Set formula”一栏中将默认的R1+E1改为R1-E1，完成含中心圆孔正方板的求解区域的划定，最后的求解区域如图11-17所示。
先在工具栏右侧的下拉菜单中选择“Structural Mech”→“Plane Stress ”，再单击工具栏中的
按钮，绘图区的图形由灰色变成红色的线条（图11-17）。
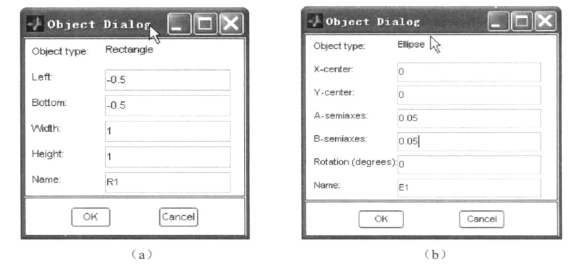
图11-16 建立几何模型
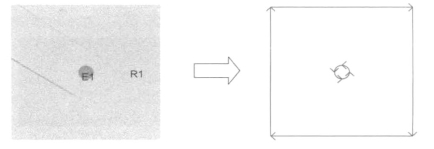
图11-17 设定求解区域及边界条件
双击红色的边界线，会弹出如图11-18所示的对话框，在“Condtion type”复选框中均选择“Neumann”，线1的“g1”改为“-100”，线2的“g1”改为“100”，其余均为默认值。注意：线5包括4条线，需要分别设置其边界条件。
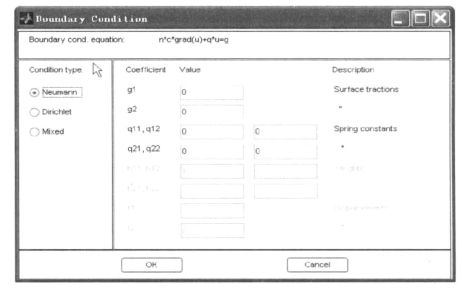
图11-18 边界条件的设置
单击工具栏中的
按钮，在弹出的对话框中完成如图11-19所示的设置。
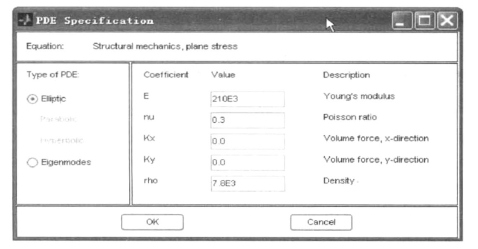
图11-19 材料参数的设置
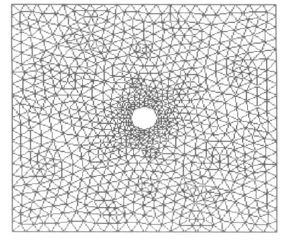
依次单击工具栏中的
按钮，完成求解区域的网格剖分。结果如图11-20所示。
图11-20 自动划分网格
（2）求解和画图
单击工具栏中的
按钮，开始解偏微分方程。
单击工具栏中的
按钮，在弹出的对话框中，“Plot type”选择“Color”和“Contour”；“Property”依次选择“x stress”和“y stress ”。单击“Plot”，则在绘图区给出如图11-21所示的x方向和y方向的应力。
图11-21 计算结果
（a）x方向应力σx；（b）y方向应力σy
根据上述应力结果，可计算得到应力集中系数。
（3）分析与思考
1）网格疏密对计算结果和计算时间的影响
计算时间与节点数即网格的密度基本成正比。一般情况下，网格越密，计算结果越好。但前面已经论述过，这种关系并不总是成立的。表11-1和图11-22为不同网格密度时计算结果和计算时间的比较，从中可以看出：开始时，随着网格密度的增加，计算精度会有很大的提高，但当网格密度达到一定程度后再增加密度，计算精度反而会有所下降。因此，在进行有限元网格划分时，选择合适的网格密度不仅能有效节约计算时间，还能够在一定程度上保证计算精度。
表11-1 不同网格密度时的计算结果和耗时
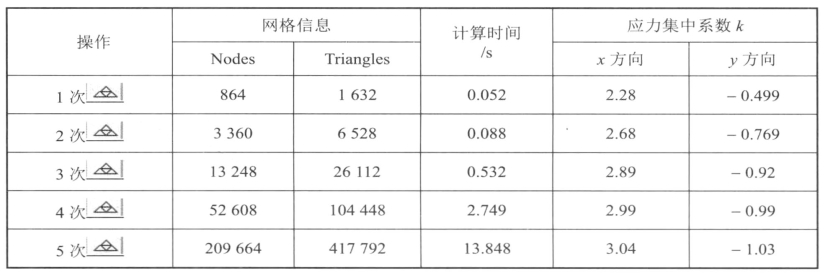
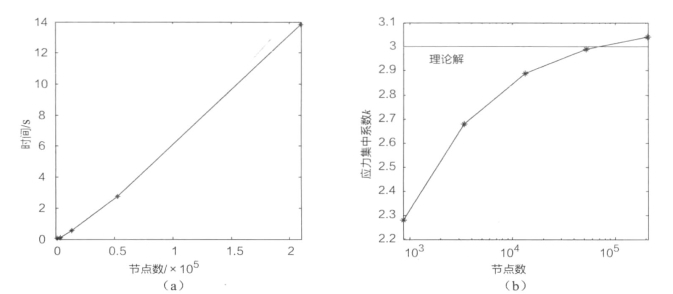
图11-22 不同网格密度时计算结果和计算时间曲线
2）如何理解工程中“无限大”的概念
固定板的尺寸，变换圆孔的直径φ，考察不同孔径下的应力集中系数。应力集中系数k随板长与圆孔直径比l/φ的变化曲线如图11-23所示（图中同时画出了含孔无限大板的理论应力集中系数，即k=3的线）。从图中可见，当l/φ较小，即孔相对于板比较大时，k与3有较大差距；随l/φ增大，k逐渐减小并接近于3；当l/φ较大时，k几乎等于3。
工程实际中并不存在无限大的结构，但有些问题（如上述问题当r很大时）可以等效为无限大结构问题，因此，弹性力学中一些无限大问题的解不只具有理论意义，也具有重要的实用价值。
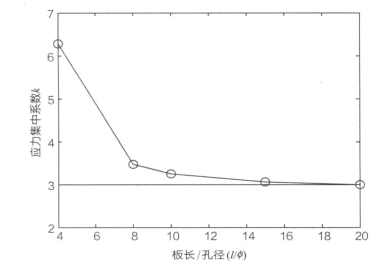
图11-23 孔边应力集中系数k随板长/孔径（l/φ）的变化