11.1.2 偏微分方程的3种边界条件
偏微分方程的边界条件在数学物理方法研究中分为以下3类。
(1)Dirichlet边界条件
Dirichlet边界条件直接给定边界上物理量的值,又称第一类边界条件。该类边界条件在MATLAB中表示为
![]()
其中,系数h和右端项r是边界上定义的函数常量。譬如,对于热钢块在恒温环境中的热传导问题,钢块表面的温度边界条件为u=T,则在MATLAB中需设定h=1、r=T。在这类边界条件中,系数r和物理量u的量纲是一致的。
(2)Neumann边界条件
给定边界上物理量的法向导数值n·(c⊗▽u),又称第二类边界条件。在MATLAB中表示为
![]()
其中,n为边界外法向单位矢量;c和g是定义在边界上的函数常量,在不同的实际问题中,它们都有具体的物理意义。以杆的受力问题为例。当一个横截面为A的杆受外力F(t)作用时,根据胡克定律可以给出如下边界条件。
受力端:
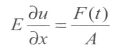 (https://www.daowen.com)
(https://www.daowen.com)
自由端:
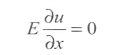
则在MATLAB中设定c=E,g=F/A或g=0即可。显然,这里的系数c和右端项g分别表示弹性模量E和面力p。
再以热传导问题为例,通常可以给定如下边界条件:
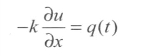
仿照前面的例子,在MATLAB中对系数项设定相应的值即可。这里的c和g分别表示导热系数k和热流密度q。如果g=0,则表示绝热过程。
(3)Generalized Neumann边界条件
在边界上的某一部分直接给定物理量的值,在另一部分则给定物理量法向导数的值,又称为第三类边界条件。在MATLAB中表示为
![]()
显然,当q=0时,上式为Neumann边界条件;当c=0时,则为Dirichlet边界条件。
MATLAB中实际上只有两类边界条件,即Neumann边界条件和Dirichlet边界条件。MATLAB将Neumann边界条件和广义Neumann边界条件统一在一起了。
