4.1.2 连续性原理与方程
1.连续性原理
在日常生活中,我们见到:河水在河道窄的地方流得快,在河道宽的地方流得慢;山谷里的风比开阔地带的风大,穿堂风比院子里的风大等。人们从上述的种种事例中总结出了一条重要原理:无论是水还是低速流动的空气,在它们流动的时候,总是在窄的地方流得快,宽的地方流得慢。确切地说,在流管切面面积小的地方流速大,在流管切面面积大的地方流速小。流速之所以随流管切面面积的变化而变化,可以用流体的连续性原理来解释。
连续性原理是研究流体流经不同截面的通道时流速与通道截面面积大小的关系(图4-3)。这是描述流体流速与截面关系的定理。当流体连续不断而稳定地流过一个粗细不等的管子,由于管中任何一部分的流体都不能中断或挤压起来,因此在同一时间内,流入截面Ⅰ的流体质量和流出截面Ⅱ的流体质量应该相等。可见,连续性原理实质上就是物质不灭定律在流体中的具体应用。
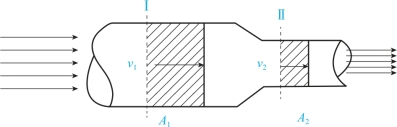
图4-3 流体连续性原理示意
根据这个原理,既然流过管子不同切面的流体质量是相等的,因此,如果流体的密度保持不变,则必然在管子细的地方流得快,管子粗的地方流得慢。
2.连续性方程
连续性原理中各个物理量之间的关系还可用数学式表达出来。空气在一条粗细不等的管内流动,在单位时间内,流过管子任意一个截面的空气质量(m),应等于单位时间内流过该截面的空气体积与空气密度(ρ)的乘积。而空气体积等于流过该截面的气流速度(v)乘以该截面的面积(A)。于是,单位时间内流过该截面的空气质量,就等于空气密度、气流速度和流管截面面积的乘积。即
![]()
式中 m——单位时间内流过任意一截面的空气质量(kg/s);
ρ——空气密度(kg/m3);
v——经过所取截面的气流速度(m/s);(https://www.daowen.com)
A——所取截面的面积(m2)。
根据连续性原理,空气流过管子任意两截面的流量应该相等,即
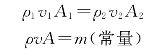
上式称为流体的连续性方程,从上式中可以看出,气流速度的大小是由截面面积和密度两个因素决定的。试验证明,在低速流动的情况下,空气密度的变化量很小。例如,在海平面高度上,飞行速度为250 km/h时,流速增大1%,密度仅减小0.04%。因此,在低速流动的条件下,通常认为密度不变,流速只与流管截面面积有关。即低速气流中的流速与流管截面面积成反比:流管截面面积缩小,流速增大;流管截面面积扩大,流速减小。这样处理可以使问题简化,计算方便,由此带来的误差很小,可忽略不计。但是,当飞行速度增大,进入高速飞行时,由流速的变化而引起的密度变化量就越来越显著,不能再认为密度不变。因此,研究高速流动问题时,必须考虑密度的变化。即流速的大小,既与流管截面面积有关,还与密度有关。
3.流体力学
流体力学为力学的一个分支,主要研究流体在各种力的作用下,流体本身的静止状态和运动状态及流体和固体界壁间有相对运动时的相互作用与流动规律。流体力学在航空器设计领域具有重要的地位,无论是何种结构的飞行器均需要考虑气动力学方面的问题。此外,流体力学由于理论基础广阔,还被分出许多分支,流体力学的主要内容包括连续性假设、质量守恒、动量定理、能量守恒等。
4.质量守恒
质量守恒的目的是建立描述流体运动的方程组。欧拉法可描述为流进绝对坐标系中任何闭合曲面内的质量等于从这个曲面流出的质量,这是一个积分方程组,化为微分方程组就是密度和速度的乘积的散度等于零。
5.能量守恒
单位时间内体积力对流体微团做的功加上表面力和流体微团变形速度的乘积等于单位时间内流体微团的内能增量加上流体微团的动能增量。
6.动量定理
经典力学包括流体力学,因此,动量定理也适用微体流元。
