4.1.3 伯努利定理
从日常生活中的许多事例可以观察到气流速度增大时,空气压力会减小;气流速度减小时,空气压力会增大。例如,向两纸片间吹气(图4-4),两纸片不是彼此离开,而是互相靠拢。就是因为吹气时,两纸片中间的气流速度增大,压力减小,造成两纸片中间的空气压力小于纸片外侧的大气压力,两纸片便在压力差的作用下靠拢。压力和流速的关系,还可用图4-5所示的风洞试验来说明。空气静止时,与试验管道各切面相连通的玻璃管内的水柱高度一样,说明各切面的空气压力相等,都等于大气压力。当在试验管右端抽吸空气时,空气就会在管道内从左向右稳定地流过。仔细观察各玻璃管水柱高度的变化,可以发现,各玻璃管水柱高度普遍上升,而且上升的高度各不同。在管径细的地方,水柱上升得更高一些,说明这里的流速较快,空气压力较小。相反,在管径粗的地方,流速慢,水柱上升得不多,说明这里的空气压力要大一些。
当空气遇上任何物体时,如机翼,空气会产生偏转,一些空气从机翼上表面通过,一些空气从机翼下表面通过。此时,空气在流动过程中会产生复杂的速度和压力的变化。要产生升力,上下表面的平均压力必须有差异才可以。
图4-4 吹气靠拢纸试验
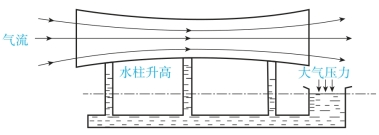
图4-5 压力和流速关系的风洞试验
伯努利的理论将流动的速度和流动中任意一点的压力联系起来。这个理论是运动和能量定律的一个特殊应用。对于管道类和轮船周围的流动来说,它是一个最基础的理论,对于空气动力学和飞行来说也是一样。(https://www.daowen.com)
想象一个平滑流动或流线型流动里面的空气微团,如果各个方向对它施加的压力都相等,那么它就处于平衡状态。如果有任何不同的压力,这个微团的平衡就会被打破,根据牛顿第二运动定律,微团要么加速要么减速。如果后部的压力大于前部的压力,速度会增加;反之,如果后面的压力小于前面的压力,速度则会减小。因此,当微团接近一个低压区时会加速,接近高压区时会减速。我们可以用另一种方法来描述这件事情,即如果流体速度降低,其压力必然升高。微团并不是孤立的,而是某个流动中的一部分,这个规律是适用每个微团的。因此,流动在接近低压或高压区时会分别加速或减速。这个原理的简单的数学表达就是伯努利定理。
试验结果表明,当流体稳定地流过一条管道时,流速快的地方,压力小;流速慢的地方,压力大。流体压力随流速而变化的这一关系是瑞士科学家丹尼尔·伯努利于1736年首先提出。因此,这一关系常称为伯努利定理。
为什么流速快的地方压力小,流速慢的地方压力大?气体压力之所以随气流速度而变化,从本质上说,是由于气流内部能量互相转化的结果。流动的空气具有动能、压力能和内能三种能量。其中,内能就是热能,即分子无规则运动的动能,它是由空气温度决定的。在低速气流中,不但空气密度变化量很小,而且空气温度的变化量也是很小的。因此,可以认为在低速气流中空气温度保持不变,即内能保持不变。这样,在低速气流中,参与转换的能量只有动能和压力能两种。
一定质量的空气,具有一定的压力,能推动其他部分的空气或物体而做功。例如,用冷气压力装置应急放下起落装置或襟翼,就是高压气体推动收放作动筒活塞而做功的结果。可见,空气因有压力而具有的一种能量,故称为压力能。空气压力越大,压力能也越大。
所谓动能,就是空气流动所具有的能量。例如,风能推动帆船前进,就是空气动能作用的结果。空气的动能与气流速度(v)和空气密度(ρ)有关。流速越大或密度越大,则空气动能越大。根据能量守恒和转换定律可知,当气流稳定地流过一条管道时,如果没有外来的能量加入,也没有能量的损失,则动能和压力能的总和不会改变,只是动能可以转化为压力能,压力能也可以转化为动能。即
![]()
可见,动能增大了,压力能必然减小;动能减小了,压力能必然增大。这就说明了为什么流速加快,压力降低,而流速减慢则压力升高的道理。因此,伯努利定理实质上就是能量守恒和转换定律在流体运动中的具体运用。
