2．2．3 逻辑函数的表示方法
对于特定的逻辑函数，可以采用不同的方法表示其逻辑功能。逻辑函数的多种描述方法是数字电路讨论的主要内容之一，也是分析和设计数字电路的基础。一个逻辑问题可以用几种不同形式的方法表示，各种表示方法之间也可以互相转换。常用的逻辑函数表示方法有以下几种：逻辑真值表、逻辑函数表达式、逻辑电路图、波形图和卡诺图等。
1．逻辑真值表
真值表是将输入逻辑变量的各种取值和相应的函数值排列在一起而组成的表格。真值表由两栏组成，左边一栏列出变量的所有取值组合，右边一栏列出对应的逻辑函数值。一个逻辑变量只有0和1两种可能的取值，所以n 个逻辑变量一共有2n种可能的取值组合。为避免遗漏，各变量的取值组合应按照二进制递增的次序排列。真值表用表格的方式列出组合逻辑系统中所有的输入变量的取值组合与输出函数值的对应关系。真值表的特点是直观明了。把一个实际的逻辑问题抽象成一个逻辑函数时，使用真值表是最方便的。真值表的缺点是当变量比较多时，表比较大，显得过于烦琐。
【例2．1】 在交通信号灯控制系统中，每一组信号灯由红、黄、绿三盏灯组成。在正常情况下，任何时刻必有一盏灯亮，而且只能有一盏灯亮，否则故障检测系统应发出信号提醒维护人员前去维修。试列出描述监视交通信号灯工作状态的逻辑电路逻辑关系的真值表。
解：设A、B、C 为输入变量，分别代表红、黄、绿三种信号灯的状态，规定灯亮时为1，不亮时为0。L 为输出逻辑变量，表示故障指示灯的状态。其中：没有发生故障时为0，有故障发生为1。对于三个输入变量A、B、C，每个变量又有0和1两种取值可能，共有000～111八种取值组合，按照题目对故障指示灯状态的描述，可见当A、B、C 全部为0或者A、B、C 中有2个及2个以上取值为1时，输出L 为1。按照上述分析可列出真值表，如表2．11所示。
表2．11 信号灯真值表
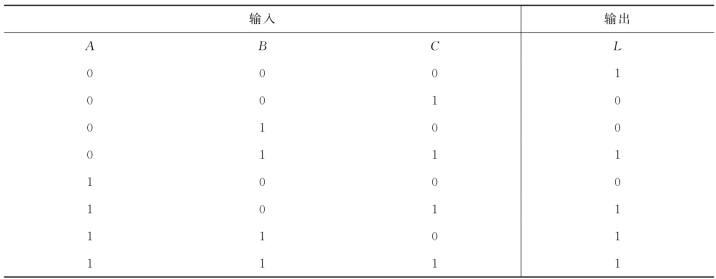
2．逻辑函数表达式
函数表达式就是由逻辑变量按一定运算规律组成的数学表达式，又称为逻辑函数表达式，即用逻辑运算符号，如与、或、非等的组合表示逻辑函数输入变量与输出变量之间的逻辑关系。具体方法为：在真值表中依次找出函数值等于1的变量组合，变量值为1的写成原变量，变量值为0的写成反变量，再将组合中各个变量进行乘运算。这样，对应于函数值为1的每一个变量组合就可以写成一个乘积项。把这些乘积项相加，就得到相应的函数表达式了。
【例2．2】 将例2．1的逻辑关系用逻辑函数表达式描述。
通过表2．11可以看到，真值表中第一行表示当输入变量A、B、C 全部为0时，对应输出量L 的值为1，应表示为
；第四行表示当A＝0，B＝C＝1时，输出量L 也为1，应表示为
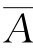BC；类似分析可见能使输出量L 为1的组合还有A
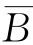C、AB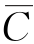
、ABC。对于上述5种组合，任意一种组合的出现都能使L＝1，即这5种组合满足逻辑或的关系，写出逻辑函数式为
3．逻辑电路图
用逻辑运算符号连接起来以实现逻辑函数的电路图则称之为逻辑电路图，即将逻辑函数式中各变量之间的与、或、非等运算关系用相应的逻辑符号图表示出来，就可以得到表示输入与输出逻辑电路图。
【例2．3】 根据例2．2的逻辑函数表达式画出相对应的逻辑门电路图。
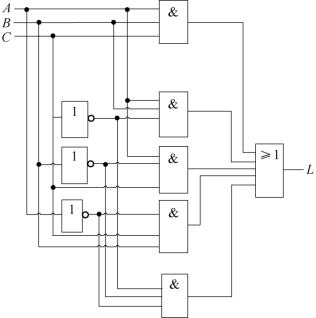
解：单个变量的非用非门实现，3个变量的与运算用3输入与门实现，各个与门的输出连接到5个输入或门的输入端即可，其相应的逻辑门电路图如图2．4所示。
图2．4 信号灯逻辑电路图
4．波形图
波形图是以数字波形的形式表示逻辑电路中输入变量与输出变量的逻辑关系。它不仅可以反映输入变量和输出变量的波形变化，而且可以反映逻辑变量与逻辑函数之间的逻辑关系。可以看到通过波形图的形式更加形象直观的观察到输入、输出变量之间的变化特点及规律。
【例2．4】 逻辑函数式的输入变量波形图图形如图2．5所示，根据例2．3的逻辑关系画出输出波形图。
解：根据题意知其逻辑函数为
根据输入和输出变量之间的逻辑关系可以画出输出波形，如图2．6所示。
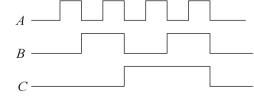
图2．5 输入信号波形图
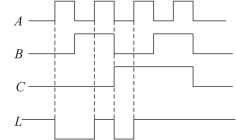
图2．6 信号灯波形图
5．卡诺图
卡诺图中的每一个小方格与真值表中第一组输入变量取值组合事实上存在一一对应的关系。从某种意义上说，卡诺图是真值表的图形表示。卡诺图不仅可以作为化简逻辑函数的工具，而且也是逻辑函数的一种方式。
将例2．4中的逻辑表达式以卡诺图的形式表示，如图2．7所示。
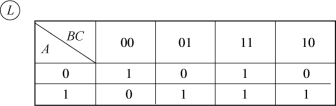
图2．7 卡诺图