2．3 组合逻辑电路分析与设计
组合逻辑电路作为数字电路研究的关键内容之一，在学习中应明确组合逻辑电路的有关概念，掌握组合逻辑电路的分析和设计方法，熟悉常用组合逻辑功能器件的基本应用及扩展应用。数字电路按其逻辑功能可分为两大类，即组合逻辑电路和时序逻辑电路。组合逻辑电路是指在任何时刻，逻辑电路的输出状态只取决于该时刻各输入状态的组合，而与电路原来的状态无关。组合逻辑电路的结构特点是：电路由各门电路构成，不存在反馈。
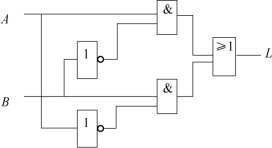
图2．16 组合逻辑电路
如图2．16所示电路图是由反相器、与门、或门构成的组合逻辑电路，其电路中无反馈。其逻辑表达式为：L＝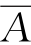
B＋A
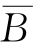。在任何时刻，只要输入变量A、B 取值确定，那么输出函数L 的值也随之确定。
描述组合逻辑电路功能的主要方式有以下几种：
1．逻辑函数表达式
逻辑函数表达式通常以与—或表达式表示，并且化简为最简与—或表达式。这种表达形式的优点是便于进行逻辑推导。
2．逻辑电路图
逻辑电路图简称为逻辑图，组合逻辑电路图是由各种逻辑门电路的逻辑符号及其相互间的连线共同组成。
3．真值表
以表格的形式描述输入变量的各种取值组合与输出函数值的对应关系。输入变量取值组合的顺序通常以对应二进制数的顺序表示。
4．波形图
波形图是以数字波形的形式表示逻辑电路中输入量与输出量间的逻辑关系。
5．卡诺图
卡诺图不仅可作为化简逻辑函数的工具方法，而且也是描述逻辑函数的一种重要方式。卡诺图中的每一个小方格与真值表中每一组输入变量取值组合事实上存在一一对应的关系。在某种意义上说，卡诺图是真值表的图形表示。
逻辑函数表达式、逻辑电路图、真值表、卡诺图、波形图是描述特定逻辑功能的不同表达形式，各种表达形式可以相互转换（图2．17）。组合逻辑电路分析主要讨论在已知逻辑电路图的条件下，通过求解函数表达式、真值表来确定所给逻辑电路的逻辑功能。组合逻辑电路设计是在给定逻辑功能的条件下，通过列写真值表、逻辑函数表达式、做出实现所需逻辑功能的逻辑电路图。因此，组合逻辑电路的分析与设计事实上是在特定的已知条件下，分析和讨论逻辑函数不同表示形式的相互转换问题。
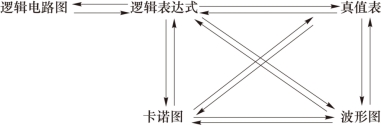
图2．17 组合逻辑电路的方式